淺談“雙減”視域下初中數學分層作業的甄選

丁虹 胡勇

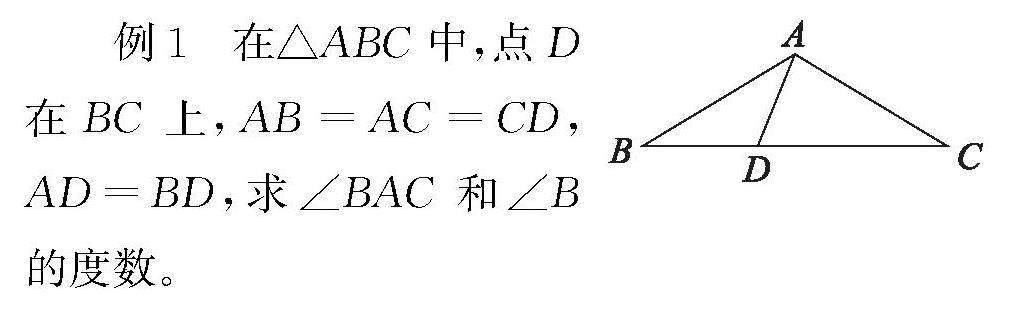
本文系合肥市教育信息技術研究課題“‘雙減背景下基于初中數學智慧作業的分層性實踐研究”的成果，課題編號為HDJ22070。

摘要：“雙減”政策對義務教育階段學生的作業負擔進行政策上的指導。但減負不減質，初中數學作業設計要充分利用分層作業，做到題目少而精，在甄選、創新題型上下功夫，重視作業評價與時俱進，從而提升學生的數學核心素養。

關鍵詞：“雙減”? 初中數學? 分層作業

《關于進一步減輕義務教育階段學生作業負擔和校外培訓負擔的意見》指出，要“健全作業管理機制”“分類明確作業總量”“提高作業設計質量”。為實現“立德樹人”根本任務，“布置分層、彈性和個性化作業”的關鍵環節在于作業的甄選設計。本文將深入研究“雙減”視域下初中數學分層作業的甄選，以期為教育實踐提供可行的建議和探索路徑。

一、“雙減”政策對初中數學分層作業的影響

第一，針對學生個體差異分層教學，滿足不同學習需求。根據學生的能力和水平進行作業的選擇和分配，這有助于培養學生的自主學習和合作學習能力，提高他們的數學核心素養。在分層作業的甄選過程中，教師可以結合學生的興趣和愛好來規劃作業內容，以激發學生的學習動力和積極性。

第二，“雙減”政策要求初中數學分層作業與教學目標、課程內容相結合。數學分層作業設計應充分考慮教學目標、課程內容，才能確保其能夠促進學生學習。

第三，減負政策的實施使得學生的學習負擔減輕，讓學生有更多的時間和精力進行深度學習，這就要求分層作業的設計必須更加精確、合理。

此外，教師還需要借助多媒體教學和在線學習平臺，提供更加靈活、多樣的教學方式。

二、初中數學分層作業的甄選原則

（一）整體性原則

2022年版的《義務教育數學課程標準》提出了“設計體現結構化特征的課程內容”的課程理念，要求學生能“體會數學知識之間、數學與其他學科之間、數學與生活之間的聯系”。這給初中數學分層作業設計提出了整體性的要求。

1．本學習領域內設計

根據新課程標準，義務教育階段的數學課程內容分為四大學習領域，整體性首先體現在本學習領域內的知識內容。例如，在設計“軸對稱圖形”第一課時的作業時，可以設計有關旋轉對稱圖形、四邊形和圓等平面幾何圖形知識的題目，促使學生在完成作業時回顧整個圖形與幾何的相關知識，體現了整體性原則。

2．跨學習領域間聯系

整體性也體現在兩個或兩個以上具有內在聯系的學習領域之間。如例1，引導學生將幾何與代數兩大領域結合，用代數方法求解三角形中角的度數問題。學生通過獨立思考、合作交流，逐步感悟數學思想。

例1? 在△ABC中，點D在BC上，AB=AC=CD，AD=BD，求∠BAC和∠B的度數。

3．跨學科領域間合作

學科融合呈現作業設計的原創精神與改革理念。例2展示了數學實踐性作業與美術學科的結合，將軸對稱圖形知識應用在美術作品的設計上，這種跨學科的作業提高了學生的綜合素質。

例2? 用剪紙或者畫畫的方式親手制作一件軸對稱美術作品。

（二）多元化原則

1.作業內容多元化

設計分層作業可以讓作業內容多元化。分層作業一般包括基礎性作業、拓展性作業和提優性作業。學生在完成作業時可根據自己的能力進行選擇，學生積極性得到保護，學習興趣也得到激發。如軸對稱圖形第二課時的作業，可設計：基礎題6道，可融入生活元素；拓展題1道，形式為解答題，以考查平面直角坐標系的應用為主；提優題1道，以折紙為主要題境。這樣每個學生都可以找到適合自己的作業，數學能力都能得到訓練。

作業內容多元化能夠促進學生各方面能力的發展，獲得數學學習的成就感，增強自信心，豐富多彩的作業內容可以提升學生學習數學的興趣。

2.作業評價多元化

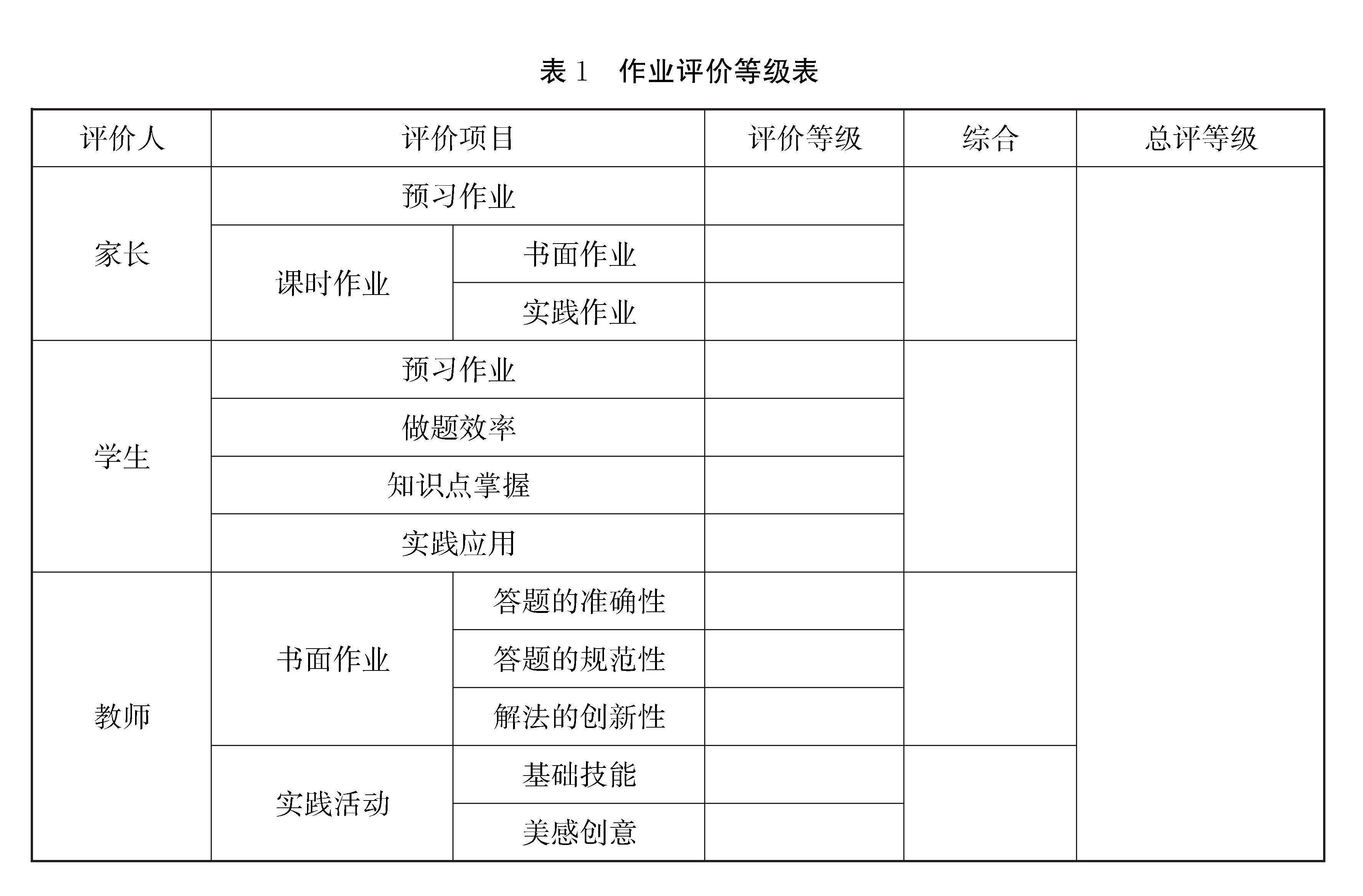
《關于加強義務教育學校考試管理的通知》提到要“完善學習過程評價”。重視學生的學習能力、表現的相對變化程度，從“培養學習習慣—觀察學習表現—發展學習能力—提高綜合素質”四個維度對過程進行考量。因學生個體能力發展水平參差不齊，教師要用相對進步程度對學生進行評價，給予學生成長的時間，而不是直接貼上標簽，避免對學生的自我效能分析產生負面影響。下面是課時作業的評價等級表（如表1）。

對學生進行評價，要讓學生在學習準備、過程及結果各個環節得到反饋，不以正確率為唯一標準，以相對變化為評價學生的新標準，建立學生學習檔案，觀察階段性變化趨勢。這樣就能解決很多學生的“瘸腿”現象，促進學生的個性化學習。

（三）創新性原則

作業中原創題的新穎性，能提高學生作業興趣，從而激發學習內驅力，達到提升學生學習效率的目的。

例3? 3月8日早上，小紅的媽媽收到了一條信息如下圖，意思是? i miss you

本題靈感來自早期收到的一則短信息。學生探索興趣盎然，利用中心對稱圖形的定義找正確的語義，幾何直觀能力及中心對稱的模型觀念得到培養。

（四）精簡性原則

設計作業的重要原則之一就是精簡。根據“雙減”精神，作業量要減少。但要達到減量增效的目標，作業就必須要精，這樣才能真正落實減負。

例4? 如圖，在已知的平面直角坐標系中，△ABC的頂點都在正方形網格的格點上，若點A、B、C的坐標分別是A（-2，1）、B（-3，3）、C（-1，4）。

①作出△ABC關于x軸對稱的圖形△A1B1C1，并寫出此時B1的坐標；

②若點P（a，b）是△ABC內任意一點，其關于y軸的對稱點是P1，求點P1的坐標；

③在y軸上直接畫出點Q，使QA＋QB最小。

（五）反饋性原則

作業設計的最后環節是收集學生作業評價的反饋情況，一是為了統計學生的學習情況，二是方便針對班級學生情況調整作業設計的效度，如下表2：

三、初中數學分層作業的甄選方法

（一）分層測評方法

通過準確評估學生的數學能力水平，可以將學生分為不同層次，從而為他們提供適合的作業內容和要求。常見的分層是根據學生的日常數學成績將學生分為優秀、良好、中等和較差等幾個層次；或者基于學生的診斷測試結果進行層次劃分，通過測試學生對數學知識和能力的掌握情況，將學生分為不同層次；還可以根據學生參與度和主動性進行分層，通過觀察和分析學生的學習態度和參與度，提供相應難度和要求的作業。

（二）多元智能培養方法

根據學生的特點，設計適合不同智能類型學生的數學分層作業，充分挖掘和開發學生的各種智能潛能，提高他們的學習興趣和動機，實現個性化、差異化的數學學習。

1.關注學生的多元智能類型

根據霍華德·加德納提出的多元智能理論，智能類型包括邏輯數學智能、空間智能、語言智能、人際智能等。教師需要充分了解學生的智能類型和特點，針對不同的智能類型進行任務設計和組織，以促進學生在數學學習中發揮其擅長的智能。

2.注重多元化的教學策略

針對不同智能類型的學生，教師可以采用不同的教學策略和方法進行數學教學。比如，對于擅長邏輯數學智能的學生，可以提供更多的邏輯推理和問題解決的機會；對于空間智能較好的學生，可以側重培養他們的幾何思維和空間想象能力。靈活運用不同的教學策略，能夠更好地滿足學生的學習需求，提高他們的學習效果和興趣。

四、總結

可采用實驗設計或長期的教學跟蹤研究，對初中數學分層作業的甄選進行驗證，以獲取更加客觀和具體的結論。學校在教研上投入更多的力量，教師在作業設計上精心甄選題目，讓學生的腳步輕盈起來，前往立德樹人的高速通道也將越來越寬。

參考文獻：

［1］孔麗麗.高中化學作業現狀的調查與實踐研究［D］.石家莊：河北師范大學，2014.

［2］中華人民共和國教育部.義務教育數學課程標準（2022年版）［M］.北京：北京師范大學大學出版社，2022.

［3］石沖.培養初中生良好數學作業習慣的研究［D］.重慶：重慶師范大學，2016.

［4］教育部辦公廳關于加強義務教育學校作業管理的通知［EB/OL］.http：//wap.moe.gov.cn/srcsite/A06/s3321/202104/t20210425_528077.html.

責任編輯：黃大燦