初中生數學閱讀能力的培養

朱義華

摘 要： 數學閱讀時掌握數學學習的前提，是順利、有效進行數學學習活動的重要基礎之一。在數學教學過程中應重視培養學生的數學閱讀，使學生逐步在數學閱讀中領悟數學的魅力。教師應指導學生閱讀，在教學過程中逐步滲透數學閱讀的方法與技巧，讓學生學會閱讀“導入”，“教學概念”，“教學例題”，以及“課堂小結”。

關鍵詞： 數學閱讀 導入 數學概念 數學例題 課堂小結

閱讀是人類汲取知識的主要手段之一，蘇霍姆林斯基說：“閱讀是對學生，尤其是有困難的學生進行智育的重要手段。”數學閱讀能力是學生的數學學習及科學學習必不可少的基礎能力和自主學習能力，是現代人必備的數學素養。因此，探索和研究符合現代人發展的數學閱讀能力具有十分重大的現實意義。閱讀教學的目的就是要培養學生獨立地進行數學閱讀的能力。葉圣陶先生說“教是為了不教”，這說明“教”是手段，“不教”才是目的，讓學生自己學會閱讀，主要是要通過課堂教學實現的。

一、學會閱讀“導入”

導入材料是每一節課都必不可少的一個環節，它起到統領本節知識的作用，每節課的數學導入往往是一個數學情境。它蘊含本節課的數學思想或方法。閱讀時要注意理解它在本節課中的具體意義，明白編者的意圖是什么，弄清楚導入知識的直觀素材，抓住關鍵的字詞句，這對于一節課的教學是至關重要的。由于學生剛剛接觸一節新授課的內容，學生會忽視導入性材料的重要，對其閱讀往往是走馬觀花，抓不住重點，因此教師在教學過程初期一定要引導學生認真閱讀導入材料。

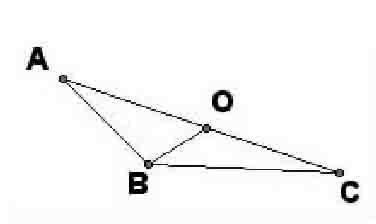
例如在教學3.4平行四邊形（八上）一節時，教材中通過一個操作題導入新課：BO是△ABC的邊AC上的中線，畫出△ABC關于點O對稱的圖形。

首先學生根據題目的要求，仔細閱讀操作中的具體要求：1.點O是AC上的中線。2.要以點O為對稱中心，畫出△ABC的中心對稱圖形。

學生根據要求回憶中心對稱圖形的相關知識，然后利用中心對稱圖形的性質，作出△ABC關于點O對稱的圖形。學生在充分閱讀理解的基礎之上，理解為將△ABC繞點O旋轉180°得到的圖形，最后得到的四邊形ABCD是一個中心對稱圖形，點O是它的對稱中心。

教師要讓學生明白一點，在這節課中，這道導入題放在這里的目的是什么？它與今天這節課有什么聯系？今天所學的平行四邊形是不是具有這樣的相關性質？帶著這些問題學生進行下面知識的學習，就能夠做到閱讀到每一點。如果學生在閱讀導入題時能夠對所學知識進行合理的“遷移”，舉一反三，與本節課的知識進行合理串聯，對本節課的教學作用就是非常大的。

二、學會閱讀“數學概念”

初中數學中有很多的概念，概念具有確定研究對象和任務的作用。數學概念不僅是建立理論系統的中心環節，而且是解決問題的前提。因此閱讀數學概念是學習數學基礎知識和基本技能的核心，閱讀數學概念要正確理解概念中的字、詞、句，能正確進行文字語言、圖形語言和符號語言的互譯。

在教學中，在學生正確理解導入材料的基礎上，引導學生進行討論，這樣得到的四邊形有什么特點，進而得出平行四邊形的概念。

什么是平行四邊形？兩組對邊分別平行的四邊形叫做平行四邊形。讓學生從閱讀平行四邊形概念中，抓住重點的字。

師：你認為在平行四邊形的概念中，哪幾個字重要？

生：兩組對邊、分別平行、四邊形。

這個時候教師結合前面的導入圖形進行概念的解釋。

師：結合圖形，想一想，你從平行四邊形的概念中能夠得到哪些結論？

（學生再次閱讀平行四邊形的概念）

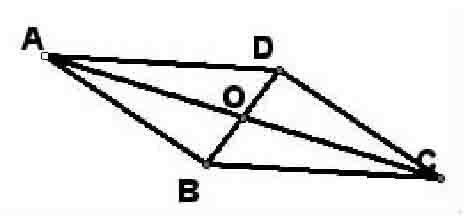
生：平行四邊形是中心對稱圖形，對角線的交點是它的對稱中心。AD∥BC、AB∥DC。

師：根據開始的導入圖形進行推導，你還能得出哪些結論？

（學生再次閱讀數學圖形，不僅提高了學生閱讀概念與數學圖形的能力，還讓學生體會到了數形結合的思想。）

生：在？荀ABCD中，點O是對角線的交點。因為平行四邊形是中心對稱圖形，對角線的焦點是它的對稱中心，所以？荀ABCD繞點O旋轉180°后，點A與點C、點B與點D分別互換了位置，旋轉后的圖形與原來的圖形重合。這樣可以得到：AD=BC，AB=DC，OA=OC，OB=OD，∠ABC=∠CDA，∠BCD=∠DAB。

最后教師根據學生的回答，總結出平行四邊形的具體性質。這樣學生在充分閱讀概念的基礎上，很容易就可以得出平行四邊形的具體性質，教得簡單，學得輕松。

由于數學概念是抽象的，因此在閱讀數學概念時，一定要堅持從學生已有的認知水平出發，結合學生的知識背景，力求做到從感知到理解，從文字到圖形，最后數形結合。

三、學會閱讀“數學例題”

在初中數學教學中，例題教學是非常重要的一環。例題具有教學功能，例題可以使學生加深對基本概念的理解，從而使概念完整化、具體化，牢固掌握所學知識，逐步形成完善的、合理的認知結構。閱讀例題時，一定要做到認真審題，分析解題過程的關鍵所在，嘗試解題，即對題目的條件和結論有一個全面的認識，掌握題目的數形特征。

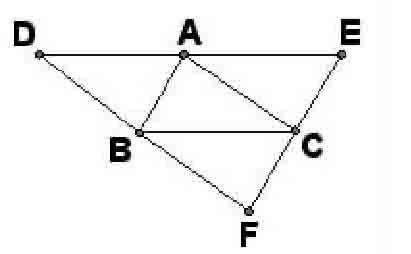
例一：如圖，EF∥AB，DE∥BC，DF∥AC，圖中有幾個平行四邊形？將它們表示出來，并說明理由。

在解決這道例題時，首先得讓學生充分閱讀題目中所蘊含的已知條件，根據前面總結出來的結論和平行四邊形的概念進行回答。

比如可以得到？荀ABCE。因為EF∥AB、DE∥BC，所以四邊形ABCE是平行四邊形。

理由：兩組對邊分別平行的四邊形是平行四邊形。

當然，在解題結束后，要通過對解題過程的閱讀，回顧和審視整個解題過程。通過總結，由特殊到一般，學生可以輕易得到？荀ADBC和？荀ABFC。這樣，既可以檢驗解題結果是否正確、全面，推理過程是否無誤，又可以揭示數學題目之間的規律性，發揮例題的“遷移”功能，收到“解一題會一類”的效果。

四、學會閱讀“課堂小結”

在一節課的最后要對本節課的內容進行小結，課堂小結的作用是鞏固已學的知識、加深對本節課知識。概念的理解，既幫助學生形成良好的認知結構，又幫助學生對本節課學習查漏補缺，鞏固提高。還可以系統地幫助學生歸納整理本節課所學的知識、方法，以及掌握知識法中反映的教學思想，溝通知識、方法間的聯系，形成所學數學內容的整體結構，進而達到提高學生學習能力的目的。

在這節課結束時，我通過投影一個平行四邊形，讓學生通過閱讀這個平行四邊形的圖形，總結本節課所學的內容。讓學生對本節課知識進行系統的總結與回顧，再次加深學生對本節課知識的印象。

所以，有效地閱讀小結對加強知識、方法的理解，對于提高學生分析問題和解決問題的能力，讓學生能夠把握知識的總體結構，構建知識的框架，領悟其中的數學思想和方法，做好典型例題的歸納和整理，培養學生的創新意識和應用能力是很有好處的。

綜上所述，讓學生具備一定的數學閱讀能力是數學學習的需要，是今后生活和繼續學習的需要。因此，我們必須重視數學閱讀能力的教學，讓數學閱讀教學內化成為學生的數學學習品質。隨著社會的發展，數學、信息技術的突飛猛進，我們必須引導學生對數學進行有效閱讀，培養學生從實際生活問題情景中發現數學問題、提出數學問題和創造性地解決數學問題的能力，提高學生的探索能力，真正體現數學閱讀在數學學習中的重要性。

參考文獻：

[1]全日制義務教育數學課程標準（實驗稿）.

[2]畢恩才.數學教學藝術論.

[3]邵光華.數學閱讀——現代數學教育不容忽視的課題.

[4]李興貴等.數學閱讀教學新論.