中高職數學教學方法比較研究

李建軍

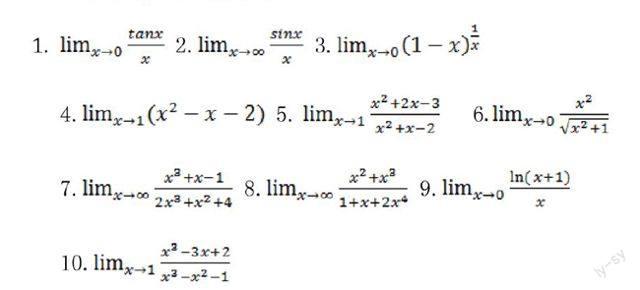
【摘 要】中高職數學教學是中高職教育的一個重要的組成部分，探求一種有效的數學課堂教學方法和教學模式是數學教師的長期任務。針對目前中高職學校學生的數學基礎參差不齊、學習積極性不高的現狀，教師應從改變傳統的教學方法入手，探討適合中高職的數學教學方法，提高中高職學生學習數學的興趣。

【關鍵詞】中高職 ? ?數學教學 ? ?方法比較

一、 聯系初等數學法

數學這門學科系統性很強，前面如果沒有學過或學得不好，那么要想學好新知識是比較困難的。這就要求我們在備課時，不但要備知識，更要備學生，使學生平穩地由初等數學向高等數學過渡。現在高職學生的數學水平都普遍較低，但是，教師沒有權利選擇學生，面對不斷變化的教學對象，只有不斷調整自己的教學理念、教學手段、教學方式，才能順利完成教學任務。

舉例說明：

如在大一新生入學后，學習微積分之前，就要復習初等數學講過的函數，函數的四個特性以及五種基本初等函數等知識。在講新課之前，從復習舊知識入手，以學生為主，教師進行引導，讓學生對五種基本初等函數的特性進行歸納與總結。目的是使學生把舊知識與新知識自然地聯系起來，達到聯舊引新的目標。

又如，在學習極限運算、積分運算中，要用到許多三角公式，很多同學對這些公式已經生疏，我們就在講新課之前提前讓學生查找公式，在講新課時就比較順暢。目前，學生的學習程度參差不齊，在教學中，要不斷地邊講新課，邊復習舊知識。這樣，才能使學習程度差的同學跟上進度。在處理新舊知識時，還應該根據每節課的教學目的、新舊知識之間的關系以及學生對舊知識的掌握情況，靈活確定。

二、授課內容與教材相結合法

我們認為，正確處理教學內容與教材之間的關系應該是將兩者有機地結合起來。既不能完全按照教材來講，這樣容易使學生感到教師照本宣科; 又不能對教材做很大修改，使學生云里霧里，抓不住重點。我們根據學生的實際情況，在教學中采取以下方式。

（1） 遵循高職高專教學“以應用為目的，以必須夠用為度”的原則，對教材中理論證明有意弱化。加強對基本理論、基本概念、基本運算的教學力度，在培養學生能力上下功夫。

（2）因為我們面對的學生在不斷更替，教材中的例題、習題無論是難易程度上，還是數量上，都有不適應學生實際的情況發生。所以，對教材中的例題、習題在前后順序、增加、減少上做適當調整是很有必要的。

（3）凡是教材中較為分散、未做概況的內容，教師應當歸納總結，提煉出要點、重點告訴學生。總之，教師應該與時俱進，對不同的學生，對教材的內容進行適當的調整和處理。

舉例說明：

例如， 前些年，我們在講“微分三個中值定理”時，不但要講清它們的內容，還要講清證明過程，這是一個難點。現在根據學生的實際，我們重點講清羅爾中值定理、拉格朗日中值定理，而對柯西中值定理只做簡單介紹。對三個中值定理的證明全部刪除，只用直觀法講清羅爾中值定理、拉格朗日中值定理成立的條件和結論，講清三者之間的關系。

三、 學科系統性教學法

數學是一門條理性、系統性很強的學科。系統性是指學科的內在聯系以及合乎邏輯的表現，而重點是指學科內在聯系的基本點、關鍵點。我們在備課時，就要確定哪些是最基本的，哪些是從屬的，再根據學生的實際情況分為詳講、略講、不講。這樣，重其所重，輕其所輕，主次分明，詳略得當。只有這樣，才能在有限的課時內，把問題講清、講透。突出重點，解決難點。

舉例說明：

例如， 在講導數一章時，我們確定導數的概念、導數的運算是重點。而復合函數求導是本章的重點，又是難點。于是我們在講復合函數求導時，先要簡單復習一下復合函數的復合步驟，然后再講復合函數求導。在講解時，要通過不同的例題，由淺入深，由易到難，多給學生想的機會、說的機會，讓他們的思維運轉起來，然后再給他們練的機會。通過以上的教學步驟，就能夠把這部分的內容講清楚了。

四、項目教學法

所謂項目教學法，是師生通過共同實施一個完整的項目而進行的教學活動，其目的是在課堂教學中把理論與實踐教學有機地結合起來，充分發掘學生的創造潛能，提高學生解決實際問題的綜合能力。即在數學的教學過程中，通過選定一些與數學緊密相關的項目活動，引導學生通過項目的實踐活動，理解和掌握課程要求的知識與技能，讓學習過程成為一個人人參與的創造實踐活動。

舉例說明：

例如，在講導數概念和導數應用這個內容時，我們改變導數定義——導數性質——運算法則——導數應用的傳統講法。把順序倒過來，先提出一個實際問題：用一塊邊長為確定值的正方形鐵皮，在其四角各截去一塊面積相等的小正方形，做成無蓋的鐵盒，問截去的小正方形邊長為多少時，做出的鐵盒容積最大？通過分析，學生用鐵盒容積與邊長的關系，建立了一個數學模型，即一個函數表達式。由實際意義看，這個函數必有最大值。這時解決問題的目標提出來了，下一步怎么辦呢？怎么求最大值呢？再進一步分析發現，由求函數的最大值問題產生去求函數圖形的單調性問題，由求單調性問題產生求函數的切線斜率問題，再由求斜率問題產生求導數的概念。再由導數的定義推出基本初等函數求導公式，求函數單調性、極值的計算方法的相關定理，最后解決這個實際問題。

五、 分類練習法

在數學教學中，講新知識的同時必須要進行適當的練習。這種練習的面比較廣，包括閱讀教科書，熟記基本概念、公式、法則，當然也包括分組討論，解題。大多是先講后練，通過練習加強對所學知識的理解和鞏固，提高學生對新知識的應用能力; 也有時是先練后講，讓同學們在練習中發現規律，然后由教師引導上升為理論。因此，講和練始終是相輔相成的。

在把握講與練時應該注意，一是既不能“滿堂灌”，又不能搞“題海戰術”。二是要把兩者有機地結合起來，注意精講與精練。精講就是要對教學內容進行優化，抓住教學的重點、難點來講，抓住基本概念、基本運算來講。

還要根據學生的實際情況、掌握程度來取舍教學內容。對學生掌握較好的，可以少講; 對掌握不好的，就應該講深、講透。在授課的過程中，要強調教師的主導作用，要注意對學生思維能力的培養，注意對他們分析問題、解決問題能力的培養。還要注重學生對數學思想、數學方法的理解。要注意培養能力的過程，不能只注重解題結果。精練就是練習不必多，但要精。要循序漸進，使練習難易程度形成階梯，或分類進行練習，也可以分層進行練習。

我們是根據同學們掌握程度不同，將習題分為A、B 兩個層次，這樣既照顧了學習程度較差的同學，使他們樹立了學習的自信心，又使學習程度好的同學不要感到“吃不飽”。在練習時，還要注意信息的反饋，在練習中發現問題，對普遍存在的問題教師要分析產生的原因，重新進行講解。通過練習使學生達到對知識的理解和鞏固，提高學生分析問題和解決問題的能力。

舉例說明：

例如，在講完極限運算之后，我們可以上一次習題課，出以下練習，讓學生在做練習的同時仔細體會運算方法并進行極限運算題型的分類：

先讓同學們進行討論，總結求極限題型的各種方法，然后對照以上題目進行歸納、分類。這時，大家積極發言，有遺漏的，有重復的，然后教師進行引導，總結出8種求極限的方法。這種先講后練，綜合練習的方式可以極大地調動同學們學習的積極性，把極限運算由一條線連起來，便于同學們學習、記憶。這樣讓學生動手動腦，有利于培養學生綜合歸納的能力。

六、 專業聯系法

中高職業技術學院，它既不是普通高等本科教育，又不是初、高中教育，它最大的特點就是“職業”二字。職業教育是以學生就業為導向，能力為本位，培養德、智、體全面發展為目標來組織實施教學的。數學作為一門文化基礎課，學生對數學知識的掌握程度不僅直接反映出一個學校的教學質量，也影響到學生專業課程的學習，同時對學生參加工作以后的學習和發展也有很大的影響。因此，在中高職院校的數學教學中，既要滿足學生學習數學知識的基本需求，也要為學生的專業課學習準備必需的數學知識。

首先，要樹立數學教學為專業服務的思想，高職教育的特點決定了數學必須具有服務性。其次，在教學過程中，我們要積極尋找數學知識與專業的結合點，使學生認識到學習數學不是孤立的，它是與學習專業知識緊密相連的。

最后，高職院校的學生來校都是抱著學技術的心態，因此，專業知識和技能的學習對他們具有較大的吸引力。而且絕大多數學生的數學基礎本身就比較薄弱，學習的天平自然會偏向專業課程。在這樣的情況下，數學教學只有將數學知識與專業課程或專業知識相融合，才能使學生在學習過程中真切感到數學是可以服務于專業學習的，從而提高學生對學習數學的興趣。

舉例說明：

如學生學習《工程制圖》需要空間想象能力; 工程造價類學生需要較強的數學運算能力; 全院各專業中許多課程都需要大量微積分，微分方程、線性代數、概率論等數學知識。

例如，講授導數應用一章中求最值一節時，我們就盡量找同學們熟悉的或是與專業有關的例子，以此培養同學們的數學應用能力。建筑力學中有許多數學模型是通過微元法建立的。在求函數的最大值與最小值時，就可以借助這些力學模型。

例題： 矩形橫梁的強度與它橫截面長的平方與寬的積成正比例。要將直徑為d 的圓木鋸成強度最大的橫梁，斷面的長寬應為多少？

解： 如上圖所示，設橫截面寬為x，長為h，則

因為橫梁強度函數為f（x）=kxh2（k為比例系數），

即f（x）=kx（d2-x2）（0

從實際情況可知，f （ x） 在（ 0，d） 內一定有最大值。

對f （ x） 求導，f' （ x） = k （ d2 - 3x2 ），

令f' （ x） = 0，得x = ± （ 負值舍去）。

七、總結

總之，每一位中高職數學教師都應從自身做起，不斷提高自身素質，在實際教學中要精心策劃每一堂課，營造良好的課堂氣氛，運用豐富的教學方法，使學生把所學到的數學知識融會貫通，使之真正變為自己的能力。如何改進教學方法并不斷提高教學質量，需要我們中高職數學教師在科學的學習理論指導下進行不斷探索和研究，從而使中高職學生全面掌握科學的學習方法，真正實現自主學習。

【參考文獻】

[1]陳杰. 五年制高職財經類專業數學教學現狀及其對策研究[D].蘇州大學，2012.

[2]龔三瓊. 高中與高職數學教學銜接研究[D].蘇州大學，2012.

[3]鄧嘉敏. 高職院校工科學生數學應用意識及其培養研究[D].湖南師范大學，2013.