高中“函數概念與基本初等函數”教學策略分析
王小振 薄志臣 張丹
【摘 要】函數是高中數學教學的重點,是學生學習的難點,因函數的相關內容與數學其他知識的關聯性很強,對學生的邏輯思維要求很高。“函數概念與基本初等函數”是高中函數教學的重要章節,文章以該章節為例,對高中函數教學策略進行探討。
【關鍵詞】高中數學;函數;函數概念與基本初等函數
一、引言
新課改的深入發展,對高中數學提出了更高的教學要求,加上學習即將接受高考,而數學是重要的考核指標,這就深化了數學在高中教學的重要性。函數是高中數學的重難點,教師在函數教學中,必須從宏觀上正確把握函數教學策略,建立切實可行的函數教學手段。
二、研究典型,準確理解函數性質
充分理解函數的性質,掌握函數的概念是學生學習好函數的重要支撐,這也是教師在教學中首要解決的教學難題。在本章節中有關基本初等函數性質的教學上,教師應該對分段函數、指數函數、對數函數和冪函數等初等函數類型的基本性質進行明確,并通過研究典型問題的方法來準確理解函數性質。如在“對數函數”的教學中,教師可以以y=log2x和y=log0.5x為代表,采用研究典型問題的方法,明確了函數的性質后,將問題慢慢過渡到對數函數y=logax的一般情況,其中a大于,且不等于1。在例題“f(x)=x+b/x(b>0)”的研究中,可以延伸出以下6個概念性質問題。即函數f(x)的定義域、值域、奇偶性、單調性、圖像以及該函數圖像與一次函數y=x和數軸y之間的位置關系。
通過開展這樣的教學,學生清楚的了解和掌握了函數f(x)=x+b/x(b>0)的性質和圖像,并將其推廣到雙勾函數f(x)=ax+b/x(x≠0)。在高中數學中,雙勾函數被廣泛的應用到其他數學知識中,如不等式、復數、數列、解析幾何等。在高中數學教學中,通過研究典型問題,不僅能準確理解該函數性質,還能良好的掌握一類函數,進而提高教學效果,幫助學生更好的理解和掌握數學知識。
三、數形結合,提高學習解題能力
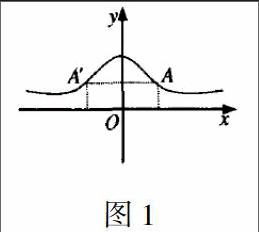
在中學階段,高中數學的抽象性要遠遠高于初中,而在高一數學學習中,學生剛從初中升入高中,抽象思維還不夠豐富,給數學學習增加很大難度。函數知識更具抽象,必須使用科學的教學方法才能更好的提高教學質量。數形結合的教學方法,是高中數學教師在函數教學中常見的方法,教師可以使用圖表法、圖像法等將一個抽象函數具體化,這在函數題目的解答中也是有重要作用的。如在“函數的奇偶性”相關知識的教學中,教師可以使用數形結合的方法進行教學。如圖1所示,曲線是函數y=f(x)所對應的圖像,設它關于數軸y對稱,點A是函數f(x)圖像上的任意一點。
由此,引出四個問題,即點A(x,f(x))有關y軸所對稱點A?的具體坐標是什么?點A?是否在函數y=f(x)圖像上?點A?的坐標還能以什么形式表現出來?除了上述三個問題,你還能發現出什么?上述4個問題構成了對函數的探究,第一個問題顯示出了點A?的坐標是(-x,f(x)),第二和第三個問題顯示出了點A?的坐標是(-x,f(-x)),問題四就是對上述三個問題的延伸,引導學生找出f(x)=f(-x)的結果,找出偶函數的基本含義。可見,圖像在引導學生學習函數知識過程中,能很好的將抽象問題直觀化和具體化。采用數形結合的方法,雖然能很好的提高學生的解題能力,但是要注意學生在解題中可能會使用幾何直觀來替代邏輯證明,所以教師要時刻觀察,以免學生產生這一的錯誤解題思路。
四、整合技術,提高數學教學質量
數學是一門極具邏輯性和技術性的學科,教師在實際教學中,可以將一些信息技術整合到課堂教學中,在豐富教學方法的同時,也能以新技術來吸引學生的學習興趣。如在指數、對數和冪函數的圖像、方程根存在性、數據擬合等教學活動中,教師可以將Excel、幾何畫板等信息技術融入教學中,引導學生使用計算器、計算機等對教學難點進行發現和探索,讓學生能更好的理解函數知識,提高數學教學質量。
如在“指數函數性質”的教學中,教師可以設計一個這樣的教學活動,即已知函數y=(1/2)x,y=2x,y=10x。問:從上述解析式中能得出什么性質?是否能確定這些解析式圖像在平面直角坐標系中的區域?這些解析式在平面直角坐標系中的具體圖像?對這些解析式的相同點和不同點進行歸納?怎么把這些相同點和不同點進行推廣?函數y=(1/2)x和y=2x有什么樣的圖像關系?在對上述問題進行教學時,教師要利用Excel、幾何畫板等信息技術把函數的圖像畫出來,幫助學生能從具體函數和對圖像的比較得到指數函數的性質。通過將信息技術整合到教學中,有效提高了數學教學質量。
五、結語
總之,為了提高高中“函數概念與基本初等函數”的教學質量,教師在實際教學中,可以通過研究典型問題,來幫助學生更好的理解函數的概念和性質,可以采用數形結合的方法和將信息技術整合到教學中,來提高教學質量。
參考文獻:
[1]許俊.高中教學策略研究——以“函數概念與基本初等函數”為例[J].文理導航(中旬),2014,34(02):19-20
[2]沙紀忠.高中“函數概念與基本初等函數”教學策略[J].上海中學數學,2012,11(06):22-23
作者簡介:
王小振(1992~),男,安徽省界首市人,工作單位:洛陽師范學院,職務:研究生,研究方向:教育評價、教學管理。

