數形結合 理解概念

牛獻禮

[摘 要]通過分析、對比、概括、推理等活動，讓學生體會小數與生活的密切聯系，并初步滲透數形結合思想和極限思想，培養學生的思維能力，增強學生對數學的理解和應用數學的信心。

[關鍵詞]小數的意義 教學設計 數形結合

[中圖分類號] G623.5 [文獻標識碼] A [文章編號] 1007-9068（2015）20-011

【教學內容】蘇教版小學數學五年級上冊“小數的意義”

【教學目標】

1.了解小數的產生源于需要，“數形結合”探究小數與分數、整數的內在聯系，理解小數的意義，會用小數表示數軸上的點，認識小數的計數單位及相關進率，體會計數單位的拓展。

2.通過分析、對比、概括、推理等活動，培養學生的思維能力，初步滲透數形結合思想和極限思想。

3.體會小數與生活的密切聯系，增強對數學的理解和應用數學的信心。

【教學重點】理解小數的意義，認識小數的計數單位和進率。

【教學難點】理解小數的意義。

【教學過程】

一、喚醒舊知，引入新課

出示“生活中的小數”：

讓學生試著讀出1.41和5.98這兩個小數。

師：小數的讀法跟整數有點區別，在讀小數點右邊的部分時，要一個數字一個數字地逐個讀出來，就像讀電話號碼一樣。

師：樂樂的身高是1.41米，說明他的身高比1米多又不夠2米，就用小數1.41來表示。牛奶的價錢是5.98元 / 盒，5.98元是多少錢呢？

生1：5元9角8分。

師：牛奶的價錢比5元多，又不夠6元，就用小數5.98元表示。生活中，在進行計算和測量時，往往不能得到整數的結果，這時常用小數來表示。

師：今天學習的是小數的意義（板書），什么是“意義”呢？我特意請教了一位知識淵博的老師——《現代漢語詞典》。在《現代漢語詞典》的第1546頁查到了對“意義”的解釋：①“表示的內容”②“價值；作用”。什么是價值呢？就是為什么要學習它。剛才我們已經有了體會，當測量和計算的結果不能用整數表示時就要用到小數。我們這節課就重點來研究“小數表示的內容”。

【思考：有效的教學建立在學生的已有知識和經驗基礎之上。課始的交流，喚醒學生對小數的已有經驗和知識，而通過介紹《現代漢語詞典》中“意義”的解釋，向學生傳遞一種足以受益終身的學習方法，體現了“授人以漁”的大學科教育觀。】

二、理解小數的意義

1.理解零點幾的意義

師（出示一個正方形）：如果這個正方形用整數1來表示，你能畫圖表示出0.1嗎？

生1：先畫一個正方形，再把正方形平均分成10份，一份就是0.1。（如圖1）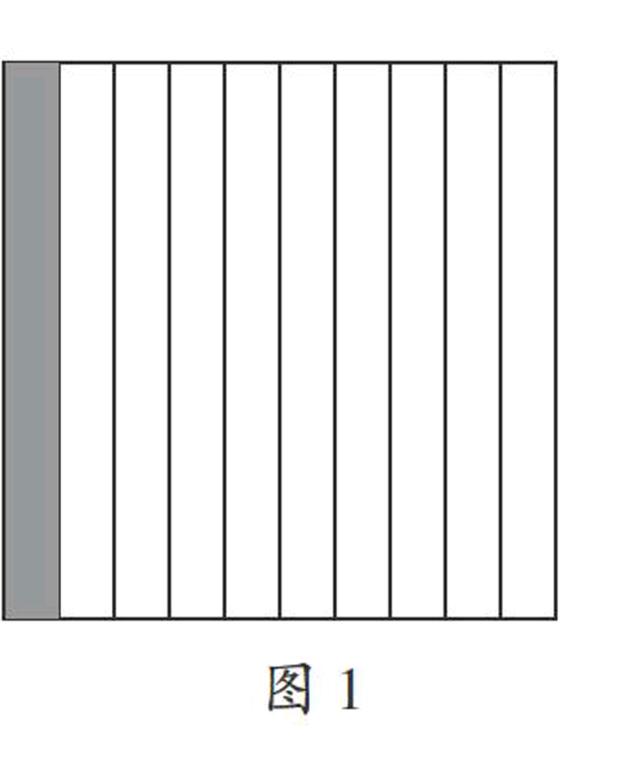

師：把一個正方形平均分成10份，這樣的一份還可以用哪一個數來表示？

生2：十分之一。

師：所以，0.1就表示十分之一，這就是小數0.1的意義。（板書）（顯示：依次把其中的2份、3份、4份涂色，讓生說出相應的小數和它表示的意義。）

（板書：0.2表示十分之二；0.3表示十分之三；0.4表示十分之四……）

師：還可以往下繼續，這些話如果用一句話來概括，可以怎么說呢？

生3：0點幾表示十分之幾。（板書）

師：在0點幾中，誰最小？（0.1）0.1也就是十分之一，就是零點幾的計數單位。現在如果把平均分成的10份全部涂上色，涂色部分是幾個0.1？（10個）也就是幾？（板書：10個0.1就是1）

2.理解零點幾幾的意義

讓學生嘗試畫圖表示0.13，然后全班交流。

生4：把一個正方形平均分成10份，先把其中一份涂色，再把第二份平均分成10份，把其中的3份涂色，合起來就是0.13。（如圖2）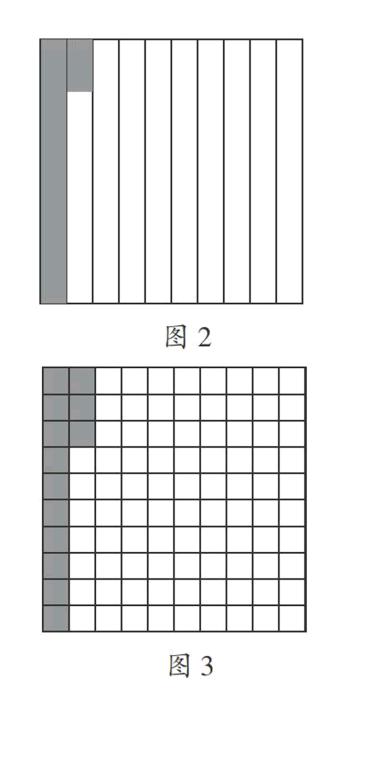

生5：把一個正方形平均分成100份，其中的13份就是0.13。（如圖3）

師：把一個正方形平均分成100份，這樣的一份是幾？

生6：0.01。

師：0.01也就是百分之一（板書：0.01表示百分之一），這就是0.01這個小數的意義。那么，0.13表示什么呢？

生7：0.13表示百分之十三。（板書）

師：0.65表示什么？

生8：0.65表示百分之六十五。（板書）

師：如果用一句話來概括，可以怎么說呢？

生9：0點幾幾表示百分之幾幾。（板書）

師：零點幾幾的計數單位是什么呢？（0.01）

師（顯示：0.10和0.1的圖示）：看圖比較一下0.10和0.1，你有什么發現？

生10：我發現0.10和0.1一樣大。

師：是的，0.10=0.1，0.10里面有10個0.01，所以——

生11：0.1里面也有10個0.01。（板書）

3.認識零點幾幾幾

師：零點幾就表示十分之幾，零點幾幾就表示百分之幾，根據這兩句話，你能推出第三句話嗎？

生12：零點幾幾幾就表示千分之幾。（板書）

師：這是我們推理出來的，凡是推理出來的還需要做一件事兒，就是“驗證”。（顯示：把一個正方形平均分成1000份，將其中的一份涂色）

生13：0.001表示1 / 1000。（板書）

（結合圖示，逐步歸納：0.002表示2 / 1000；0.003表示3 / 1000；0.004表示4 / 1000；……）

師：0.001就是零點零零一，10個0.001是0.01。（板書）

師（歸納）：小數就是表示十分之幾、百分之幾、千分之幾……的數。

【思考：有效地利用已有知識經驗，啟迪學生進行探索和發現。此處的正方形作為思維表象的載體，通過平均分形象地展現小數形成的過程，并為學生提供了有效理解小數意義的表象模式。借助直觀的圖示，溝通小數與十進分數（分母是10、100、1000……）的內在聯系，把小數的概念建立在十進分數的基礎之上，使學生在與分數的聯系中理解小數的產生，初步理解小數的意義。】

4.用數軸上的點表示小數

出示：數軸

師：這是一條帶方向的直線，數學上叫做“數軸”。任意一個小數都能用數軸上的點來表示，箭頭向右，表示從左往右，數軸上的數越來越大。怎么用數軸上的點表示0.6呢？

生14：把0到1這一段平均分成10份，取其中的6份就是0.6。（課件演示：在數軸上表示出0.6。）

師：0.61應該在哪里呢？要準確地找到它的位置，應該怎么辦呢？

生15：把0到1平均分成100份。

生16：也可以把0.6到0.7平均分成10份。

師：把0.6到0.7這一段平均分成10份，其實就相當于把0到1這一段平均分成了100份。（課件演示：把0.6到0.7這一段放大后，再平均分成10份，表示出0.61）

師：如果要在直線上表示0.618呢？

生17：再把0.61和0.62這一段平均分成10份。

師：也就是把0到1平均分成——

生18：1000份。（課件演示：把0.61到0.62這一段放大后，再平均分成10份，表示出0.618）

師：如果我們想表示得更精確，還可以怎么辦？

生19：繼續分下去。

師：想一想，0和1之間有多少個小數？

生20：無數個。

師：0.6和0.7之間呢？

生21：也是無數個。

生22：任何兩個數之間都有無數個小數。

師（追問）：為什么？

生23：因為還可以一直分下去。

師：沒錯！還可以無限地分下去，就會有無數個小數。這里我向大家隆重介紹0.618這個小數，0.618是一個非常神奇的小數，大家可以課后了解這個小數。

【思考：借助“數軸”這一直觀模型，數形結合，從整數到一位小數，再從一位小數到兩位小數，再到三位小數，讓學生直觀感受到一個不斷細分的過程。學生通過觀察不斷細分的數軸，能感受到小數表示數的精確性，感悟到用更小的計數單位可以進行更精確的表示。】

三、鞏固應用，深化理解

1.“數數”練習

介紹：數學家華羅庚的名言“數是數出來的”。

（1）以0.1為單位數數

結合圖示，讓學生依次數出0.1、0.2、0.3、0.4。

顯示：0.4的計數單位是（ ），它有（ ）個這樣的計數單位，再添上（ ）個這樣的計數單位，就是1。

（2）以0.01為單位數數

結合圖示，讓學生依次數出0.01、0.02、0.03、0.04、0.05、0.06、0.07、0.08、0.09、0.10、0.11、0.12。

顯示：0.12里面有（ ）個0.01，還可以說0.12是由（ ）個0.1和（ ）個0.01組成的。

結合圖示，讓學生依次數出：0.97、0.98、0.99、1、1.01、1.02、1.03。

1.03里面有（ ）個0.01，還可以說1.03是由（ ）個1和（ ）個0.01組成的。

2.寫出數軸上箭頭所指的數

0.4 （ ） 1.3 （ ） （ ）

■

【思考：“數數”活動是學生形成“數概念”的基礎，沒有“數數”這一過程，學生對“數”的理解是不深刻的。通過觀察圖形中直條的累加，也就是計數單位的不斷累加，不斷形成新的小數，學生按照計數單位一個一個地數數的過程中，感知小數的組成。在遇到“拐彎數”時，教師應放慢速度，不斷加強演示，讓學生直觀感受到“滿十進一”，為學生掌握數的組成和相鄰計數單位之間的十進制關系提供了形象的支撐。】

四、全課總結

（責編 金 鈴）