善用比較策略 提升學生思維品質
胡春燕
【摘 要】俄國著名教育家烏申斯基說:“比較是一切理解和思維的基礎,我們正是通過比較來了解世界的一切。”在小學數學教學中,比較是經常使用的一種有效教學策略。合理使用比較策略,不僅能幫助學生深入理解數學知識,還能有效提升學生的思維品質。
【關鍵詞】數學教學;比較策略;思維品質
一、比較的內涵與外延
1.同中比異,揭示本質。
小學教材中,很多知識的差異性常常被他們的相似性、相近性和相關性所掩蓋,小學生在思想上易被泛化為同類事物而發生混淆。此時組織辨異比較,有利于學生區別知識的各自內涵。如教學小數的讀法,課始要求學生讀出507.507,通過學生正誤讀法比較引導明確:整數部分要讀出計數單位;小數部分只要讀出各數位上的數就行了。接著又讓學生讀:5007.5007,再次比較明確整數部分連續兩個零只讀一個零,小數部分要把零一個個都讀出來。兩次辨異比較,學生清晰掌握整數部分和小數部分的不同讀法,從表面上的“同”辨出讀法上的“異”,輕松突破難點。
2.異中比同,深化理解。
數學知識靈活多變,對那些隱而不顯的知識共性,習慣于表面現象認識事物的小學生誤以為他們是各各獨立。此時組織異中求同的比較,則有利于挖掘知識的共性,使學生的理解深刻化、概括化。如學習了約分和通分后,學生的理解往往分割地停留在“兩種過程”、“兩種方法”的孤立認識上。如適時組織比較,讓學生悟出約分和通分盡管過程、方法不同,但都是分數基本性質的應用,只是索取角度不同,前者取“同時縮小相同的倍數”,后者取“同時擴大相同的倍數”,能把學生的理解引向深入、引向概括。
3.同中比優,促進優化。
面對相同的問題,不同的學生會產生不同的思維活動,從而產生不同的思維方法,而不同的方法是不同思維層次的體現,究竟應該選擇怎樣的方法,這就需要橫向比較,沒有比較就會固步自封。比如在探究長方形的周長時,方法有 “長+長+寬+寬”,有“長×2+寬×2,有“(長+寬)×2”。教師應引導學生進行優劣繁簡的比較,促進學生知識理解的準確性、深刻性和概括性,實現發散思維和聚斂思維的和諧結合。
二、善用比較,提升思維品質
1.通過比較實現有效遷移,提升思維的靈活性和條理性
比如在教學《比的基本性質》時,教師可先復習商不變的規律、分數的基本性質以及除法、分數、比之間的聯系,然后引導學生大膽猜想:既然比和分數和除法之間有這么密切的關系,分數中有基本性質,除法有商不變的規律,敢不敢對比中存在某種規律進行大膽猜想?在猜想的基礎上引導學生舉例驗證,從而得出比的基本性質。
2.通過比較促進抽象概括,提升思維的抽象性和嚴密性
比如教學蘇教版五上《分數的意義》一課。為使學生建構分數的意義,教學中設計兩次比較。
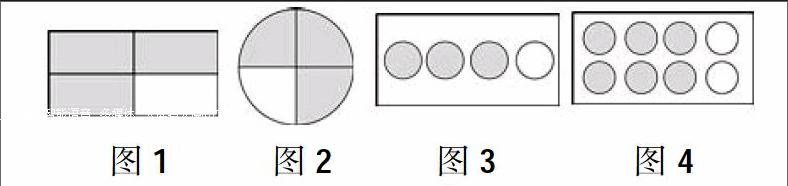
圖1 圖2 圖3 圖4
師:為什么這4幅圖都可以用■表示?
師:比較前兩幅圖與后兩幅圖有什么不同的地方?
通過兩次比較分別讓學生明確:平均分的份數一樣,涂色的份數也一樣,就可以用同一個分數表示;單位“1”可以是單個物體或圖形,也可以是多個物體或圖形組成的一個整體。
通過比較幫助學生逐步抽象出分數的本質屬性“怎么分”和“分什么”的問題,進而概括出出“分數的意義”。這樣的比較歸納過程,是學生認識上質的飛躍,從感性到理性、逐步把握概念的本質,促進思維的深度理解和高度概括。
3.通過比較研錯糾錯,提升思維的精確性和深刻性
數學教學中,有許多知識點容易造成混淆,錯誤在所難免。為使學生能清晰地分辨知識的本質屬性,可以將錯解和正解對比,引導學生辨析反思,促進學生自主糾正。
如教學乘法分配律后,由于與乘法結合律的相互干擾,計算25×44時,錯誤極多。教學中,可呈現正解和錯解,引導學生進行“形”辨和“意”辨:25×(4+40)既有加法,又有乘法,是分配律(a+b)×c=a×c+b×c的形式。“意”是指算理的理解:25×44表示44個25,即4個25加40個25。由此推斷前者是錯誤的。
25×44 25×44
=25×(4+40) =25×(4+40)
=25×4+40 =25×4+25×40
=140 =1100
通過比較辨析, 使學生逐漸把握乘法分配律的本質內涵,把新舊知識融會貫通,明晰易混淆的概念。同時,學生的思維經歷了反省、自悟的過程,理解深刻,記憶清晰。
4.通過比較促成知識建構,提升思維的廣闊性和綜合性
比如六上學習了分數應用題后,時常會出現這樣的問題:“桃樹和梨樹一共有96棵,梨樹的棵樹是桃樹的■,桃樹與梨樹各有多少棵?”
解法一:用方程解。設桃樹有X棵,梨樹有■X棵,X+■X=96
解法二:看成求單位“1”的分數問題解。96÷(1+■)先求出單位“1”桃樹的棵樹。
解法三:轉化成按比例分配解。“梨樹棵樹與桃樹的比是1:3”,用96÷(1+3)先求出梨樹的棵樹。
解法四:轉化成已知單位“1”的分數問題解。“桃樹棵樹占總棵樹的■,梨樹棵樹占總棵樹的■”。96×■求出桃樹棵樹,96×■求出梨樹棵樹。
教師可對比講評,引導學生理解各種方法的解題依據,感知方法優劣,選出適合自己的最佳解法。同時比較解法一和解法二,明確求單位“1”的問題可以方程解,也可以用除法解。比較解法二、解法三和解法四,讓學生充分理解比、分數、除法之間的內在聯系。如此多方位、多角度的比較,既有利于培養學生思維的靈活性和獨創性,又有利于知識的縱向溝通,發展思維的廣闊性和綜合性。
比較是思維經歷頓悟、鑒別、飛躍的過程,是辨析、溝通、建構的過程。在小學數學教學中,合理運用比較策略,既有利于學生把握數學知識的本質,形成結構化的知識網絡,又有利于發展學生的數學思考,提升學生的思維品質。
(作者單位:江蘇省蘇州工業園區婁葑學校)

