淺析多元化探究方式下的生本教學

陳瑜

[摘要]素質教育改革一直致力于以生為本教學行為的實踐和研究，在以生為本教學行為開展的過程中，探究式學習成為一道靚麗的風景線，也引發了無數一線教師和教育科研專家的深入實踐和研究，初中數學亦是如此.

[關鍵詞]以生為本；探究；自主；合作；啟發

學生學習應當是一個生動活潑的、主動的和富有個性的過程.在這個過程中，教師要充分結合我們所開展的數學活動內容，迎合學生已經建構起來的知識與技能，結合學生在學習過程中可能存在的興趣點，從而激發學生在整個數學活動過程中的參與度和思維度，達成真正的以生為本的教學行為.

探究學習是一種非常有效的教學行為，它不僅從學生的參與形式上滿足了學生的興趣，激發了學生的參與度，更從探究的內容上引導了學生的思維，訓練了學生的能力提升.而為了進一步提升探究的效果，進一步達成以生為本的教學理念，筆者結合人教版數學教材中的實例談一談如何對探究學習進行細分，從而采用多元化的探究方式達成更好的生本教學.

自主探究、激發思維

自主探究是學生通過自己的觀察和思考發現生活中、學習中的數學問題，并結合學生已有的知識與技能進行進一步自發的問題分析和問題探究，最終解決問題，并服務于學生新知識與技能的建構，服務于實際問題的解決，甚至影響學生的后續學習，促使可持續提升.

自主探究學習的真正開展需要教師在平時的教學過程中積極創設符合教學內容開展、教學目標達成的多種情境，讓學生因為情境的存在而對情境產生興趣，并善于采集、篩選情境中的信息，發現其中的問題，進行一系列的問題解決的行為.

比如在《圓與圓的位置關系》的學習過程中，為激發學生對圓與圓的位置關系的直觀感受，我們先給學生提供一部分生活中能反應圓與圓位置關系的實例，如圖1所示.

在學生建立初步的感受以后，教師再提問學生：你們能結合生活經驗，再舉出一些能反應圓與圓位置關系的例子嗎？這時，教師放手學生讓他們去思考、交流、共享等，這個過程中，學生會呈現以下三個自主探究的思維過程：

（1）自主認知.學生會對教師提供的實例進行一個自主認知的過程，在這個過程中，學生在思維中會初步構建一個圓與圓位置關系的認知.

（2）自主對比學生結合自己的認知，對自己生活經驗中圓的實例進行對比和篩選，以此提升學生對圓與圓位置關系的認知.

（3）交流提升.學生把自主思考后構建起來的實例提供給大家交流，交流的過程是一個再次認知和判定的過程，并通過交流提升完善學生對位置關系的認知和判定能力，能有效地服務于后續活動的開展.

合作探究、全面提升

合作探究是學生在初中數學學習過程中常用的一種探究形式，每個學生在合作的小組中擔當不同的任務和相同的使命，而不同任務是因為學生個體和學習內容所決定的，相同的使命是合作競爭中所產生的強烈的集體榮譽感和競爭意識.這種合作探究大大提升了我們的教學效能，具體可以從以下兩個方面來深人體現.

1.生本教育，全面發展

在合作探究的過程中，不同的任務是由探究的內容和學生個體共同決定的，在整個合作小組中，首先我們的探究內容需要不同的人去完成不同的任務，而相應的任務對學生的學習能力和學習態度都有不一樣的要求，在合作探究的過程中，分工協作是必須的，因此，在分工合理的前提下進行各種任務的完成，我們的合作探究才可以達成真正.的生本教育，全面發展的理想效果，比如在函數性質的建構中，無論是一次函數還是反比例函數，我們都引導學生經歷數據和信息的采集，數據和信息的轉換，規律和結論的分析，論證探究過程等，這些不同的過程對學生的能力要求是不一樣的，在整個合作探究的過程中，進行巧妙的分工能確保每個學生都有事情做，這些不同思維難度的內容需要不同思維能力的學生去完成，每個學生都參與不同程度的思維活動，這樣既能有效協調好探究的各項工作，還能達成隱性分層的效果，有效激發每個學生的參與度和思維度，促使每個學生的提升和發展.

2.合作競爭，激發潛能

在合作探究的過程中，每個學生都是小組的個體，小組內部本身就是一個競爭的小組，每個學生都因為在小組中的存在而努力去達成相應的任務和存在價值，而大家又都會去努力為自己的小組增光添彩，提升自己的小組的團隊競爭力.

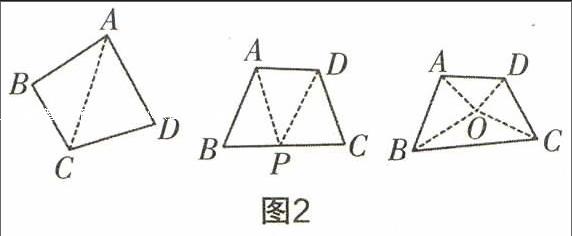
比如我們在人教版《多邊形的內角和》的教學過程中，我們引導學生進行四邊形內角和的猜想與證明，學生通過獨立思考和分析進行證明和交流，學生在小組合作和交流中分工完成對四邊形內角和的證明，而學生在交流的過程中卻發現，方法不止一種，如圖2所示，是部分小組合作后生成的證明方法.

每個學生都參與到內角和的證明之中，而不同層面的學生能想出不同的方法，多種方法的呈現讓每個學生的興趣和思維再次提升，學生組內會想出多種方法來證明四邊形的內角和，并帶著類似的方法去證明多邊形的內角和.在整個過程中，不同層面的學生分別對四邊形和多邊形的內角和的證明進行了不同的思維活動，都在積極建構屬于自己的正確認知.雖然他們建構的深度不同，比如方法的不同，證明思維方法的差異，但是都在他們原有的基礎上得到了較大的提升.其實在這個合作的過程中，學生想出來的方法是多種多樣的，而應用方法的數學思想卻是一樣的，那就是我們數學中常見的化歸思想.在教學實踐的過程中，我們引導學生對多種方法進行分析和類比，提升學生對學習行為的自我分析和總結，提升學生的學習能力，挖掘學生在平時生活和學習中的潛能，

總而言之，在合作探究的過程中，每個學生都為了完成探究目標而努力，無論是小組成員中的個體，還是整個小組團隊，都在合作中進行著默默的競爭，都為了榮譽而努力思考，形成良性循環，

啟發探究、逐一突破

在初中的探究性學習過程中，有很多的學習內容僅憑學生的能力和思維很難構建正確的結論或規律，將這樣的探究放在課堂上讓學生去完成，很有可能變成放羊式的探究，許多學生因此而失去探究的目標和興趣，更無法促使教學目標和教學任務的完成.因此，啟發式探究在初中數學教學過程中就必不可少了.教師采用問題啟發、巡視點撥、難點啟發等方法來幫助學生對探究活動實現逐一突破，不僅幫助學生完成了探究的目標、突破了探究難點、建構了探究認知，還幫助學生積累了一定的探究方法和經驗，促使學生的數學思想在數學學習中不斷積淀。

比如在《直線和圓的位置關系（2）》的教學過程中，我們的教學目標就是讓學生通過探究理解并掌握切線的判定定理和理解并掌握切線的性質定理，而在這個探究的過程中，學生很難運用已學的知識和技能進行獨立探究或合作探究，為此，我們就要給學生創設情境，利用問題引領的方法來啟發學生進行啟發式探究，達成逐一建構、逐一突破的效果，達成知識與技能、思想與方法雙重遞進的效果，

思考1：如圖3，在⊙0中，經過半徑OA的外端點A作直線l⊥OA，則圓心0到直線Z的距離是多少？直線l和⊙o有什么位置關系？

啟發目的1：啟發學生建構切線的判定定理.為了啟發學生建構較為嚴密的判定定理，我們可以采用填空的形式來引導學生總結和歸納，如：經過____的外端并且____于這條半徑的直線是圓的切線，

思考2：將思考1中的問題反過來，如果直線l是⊙0的切線，切點為A，那么半徑OA與直線Z是不是一定垂直呢？

啟發目的2：啟發學生采用逆向思維的方法進行進一步的思考和分析，從而理解切線的性質，建構切線的性質定理.同樣為了達成較為嚴謹的切線的性質定理，也是采用填空的形式來建構，如：圓的切線____于過切點的____，

在我們平時的教學過程中，探究學習的方式不是一概而論的，也不是一錘定音的，教師首先要結合教學內容和學生的實際情況預設好相應的探究方法，預設以后還要充分實踐，在實際的教學過程中也要隨著學生的實際生成情況而隨機應變，比如學生合作探究過程中，學生的思維得不到很好的生成，此時我們就要適度地啟發學生，利用問題等形式進行啟發，以此促使學生探究思維的展開，促使學生達成探究任務，建構知識與技能.endprint