數形結合思想的應用

朱梅

摘 要： 數形結合即根據數與形之間的對應關系，通過數與形的相互轉化解決數學問題的思想.化數為形；化形為數，數形結合是數學探究和解決問題的重要手段，在高中數學中占據著重要的地位.這種思想可以使某些抽象的數學問題直觀化、生動化，能夠變抽象思維為形象思維，有助于學生把握數學問題的本質.

關鍵詞： 數形結合 高中數學 解題應用

數形結合思想作為高中解題的一種常用思想方法，幾乎每一章節的學習都離不開它的身影.

一、集合中的數形結合

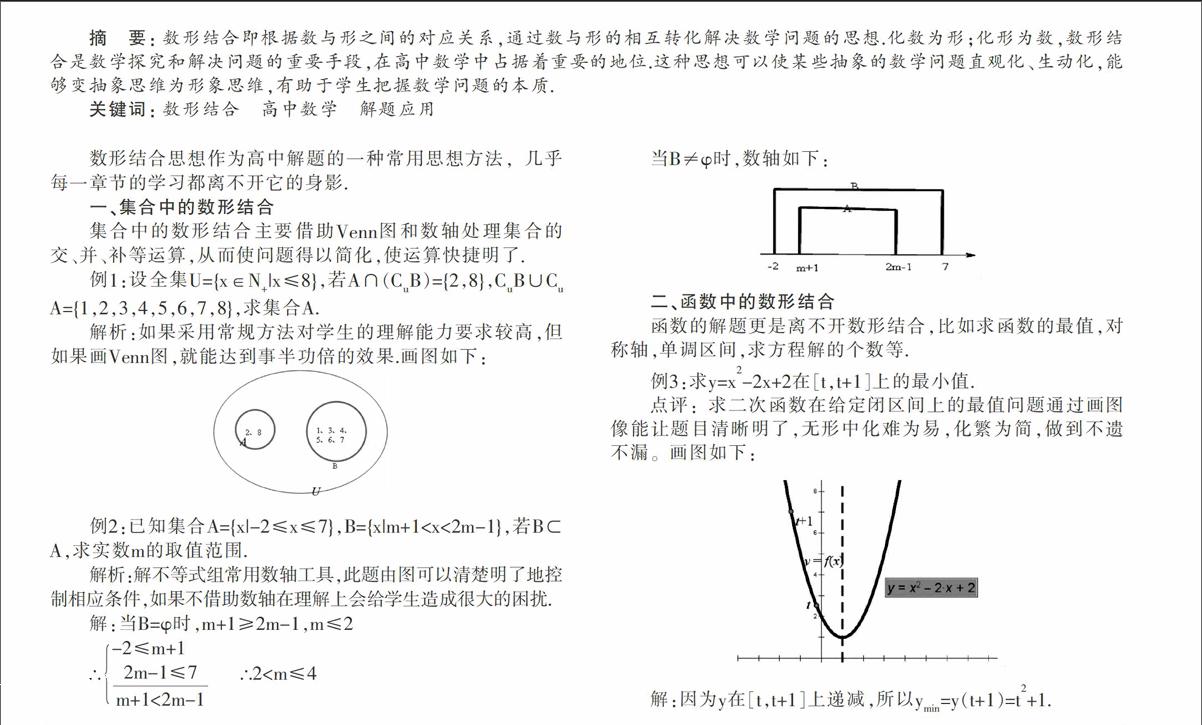
集合中的數形結合主要借助Venn圖和數軸處理集合的交、并、補等運算，從而使問題得以簡化，使運算快捷明了.

例1：設全集U=

點評：解決幾何概型的概率一般利用圖形輔助解題.分析題目畫好圖形，找到對應區域，則P=面積之比或長度之比或體積之比等.

數形結合的思想，其實質是將抽象的數學語言與直觀的圖形結合起來，實現問題與圖形之間的相互轉化，從而達到化繁為簡，化難為易，逐步降低難度來解題的目的.

數形結合滲透在高中數學的各個角落，在解題中老師要講透這種“數”與“形”關系的轉化，啟發學生深刻認識數學問題的實質，才能將知識轉化為能力，才能提高學生靈活運用數形結合思想解決問題的能力.