類比法在高中數學教學中的有效應用
【摘 要】探討類比法在高中數學知識教學、復習課教學、解題教學中的具體應用。
【關鍵詞】類比法 數學教學 有效應用
【中圖分類號】G 【文獻標識碼】A
【文章編號】0450-9889(2016)03B-0106-02
數學史告訴我們:許多關鍵時刻,數學家巧妙地運用類比推理從而得到數學的新發現,在科學道路上,獲得巨大的成功。天文學家開普勒說過:“我珍視類比勝于任何別的東西,它是我最可信賴的老師。”數學家拉普拉斯說:“甚至在教學里,發現真理的工具也是歸納和類比。”可見類比法常用于科學研究領域,如果把它作為一種思維方法應用在教學中,也是行之有效的。
數學知識與數學方法存在著大量相似的地方。在中學數學中,可類比的東西很多,教師若能很好地把它應用在教學中,讓學生嘗試運用,那么它在數學學習中會起到事半功倍的作用。
一、什么是類比法
類比法,也稱類比推理,是根據兩個或兩類事物有部分屬性相同或相似,推出它們在其他屬性上也可能相同或相似的思維推理方式。它是一種從特殊到特殊的推理,當兩者共同屬性越多,推理的正確度越高。
二、類比在高中數學教學中的有效應用
(一)在知識教學中的應用
1.橫向類比,加強學生對知識的理解和記憶
中學數學教材中有一些相近概念是難于讓學生理解和接受的。倘若在學習新知識時我們通過橫向類比,發現新舊知識的相同點,利用已有的舊知識,來認識新知識,會使學生更加容易理解新知識,同時也能突破教學難點,降低教學難度。
如,學習高中“映射”概念的時候,我們可以類比函數的概念,兩者的概念均要求:對應關系中集合 A 中的任意一個元素在集合 B 中都有唯一一個確定的元素與之對應,不同之處是函數中的集合 A、B 是非空數集,映射中的集合 A、B 是非空集合。這樣的類比,使原本難于理解的定義更清晰,并且理清了兩者的關系——函數是特殊的映射。
因為類比物具有某種相似性,所以只要記憶其中一類事物的某一屬性,就容易記憶另一類事物的相似屬性。例如,在等差數列{ an }中,有如下性質:
還有,如果 sn,s2n-sn,s3n-s2n,…成等差數列,那么可以類比得出 sn,s2n-sn,s3n-s2n,…成等比數列。
只要熟記等差數列的性質,等比數列的相應性質也隨之熟記。
由此可見,引導學生應用類比法得出新知識,同化新舊知識,便于記憶。
2.縱向類比,引起猜想,深化和拓展知識,激發學生的學習欲望
縱向類比,如平面向量與空間向量、平面幾何與立體幾何的某些對象類比等,數學知識在延伸拓展過程中常借助比較、聯想,啟發和誘導學生以求思維的變異與發散。在教學過程中,引導學生應用類比法,利于在已有知識、經驗的探索中歸納和總結出教材中的定理、公式,深化與拓展學生的知識。
例如,三棱錐的教學,總結出如下公式。
由表格前三行結論類比可知,平面三角形對空間三棱錐,線對面,長度對面積,一半對三分之一,我們可以大膽猜想內切圓相對應內切球,從而在空白處可填“三棱錐的體積等于其內切球半徑與三棱錐表面積的乘積的三分之一”。當猜想被證明成立后,將會誘發學生主動探索的欲望與熱情。這便是一種新知識“再發現”的體驗。在探索結果的同時,既使知識得到深化,又使內容得以拓展。
(二)在復習課教學中的應用
運用類比揭示知識的聯系,使知識系統化,網絡化。數學知識點很多,類比法可以作為知識聯系的橋梁,使知識脈絡清晰。如老師在章節復習時,可將各個知識點綜合起來,通過類比使零散的知識系統化、網絡化,這樣則有利于學生全面掌握。如在高中解析幾何的圓錐曲線一章中,橢圓、雙曲線、拋物線的知識中存在著同一性與差異性,所以教材在章節復習中,引入一個圖表,將三種圓錐曲線的方程形式、圖形、頂點坐標、焦點坐標、離心率等這些內容的同與異,一目了然地呈現在學生面前,便于學生類比記憶。
(三)在解題教學中的應用
1.將數學知識間類比,引導學生積極探求解題思路,克服盲目性
數學家波利亞說:“類比是一個偉大的引路人。” 當我們運用通式通法解決不了某些數學問題時,可以大膽地尋找與題目條件結構相類似的定理、公式進行類比,轉化為另一知識結構的數學問題,從而突破題目難點,探求到新的解題方向,使學生的思維寬度得以拓展提升。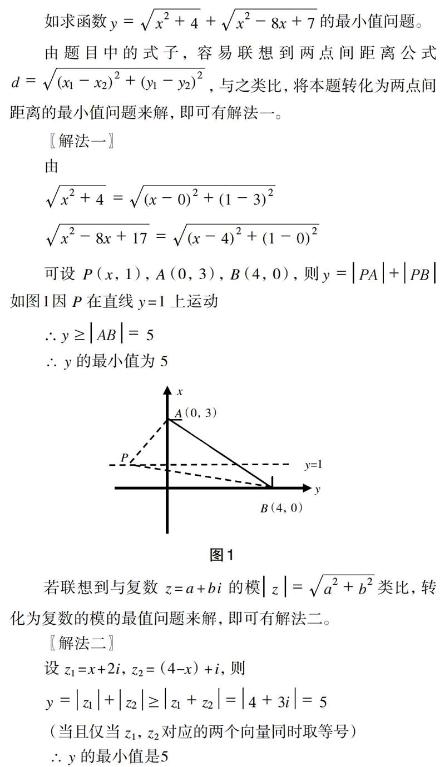
如求函數的最小值問題。
由題目中的式子,容易聯想到兩點間距離公式,與之類比,將本題轉化為兩點間距離的最小值問題來解,即可有解法一。
〖解法一〗
若聯想到與復數 z=a+bi 的模類比,轉化為復數的模的最值問題來解,即可有解法二。
由此可見,解答數學題時應用類比進行思維分析,會克服盲目性,并能快速獲取思路和方法,提高解題效率。
2.跨學科類比,拓寬學生解題思路
宏觀世界的學科內容彼此相互聯系,如果能將其他學科的特性運用到數學學科中來,將會收到意想不到的奇效。如與物理光學性質結合解題的例子。
〖例〗如圖2,設F1,F2 是橢圓的兩個焦點,l 是橢圓的切線,A是F1 關于 l 的對稱點,求證:。
〖分析〗常用的方法,先設出切線的方程,再根據對稱性求出點A的坐標,最后由兩點間距離公式求,思路清晰但計算相當復雜。若能聯想到橢圓的定義,將問題轉化為先證F2,P,A三點共線,再聯想到與物理學科相關的橢圓光學性質知,由對頂角有,因此,證明便容易。
總之,在中學數學教學中若能靈活地運用類比法,并有意識地培養學生的類比思維,則不僅能幫助學生有效地掌握數學知識,提高解決數學問題的能力,而且還能使學生的理性思維達到新的境界。
但我們要注意,類比是一種似真推理,必須要經過嚴格的邏輯論證,才能確定猜想的正確性。同時這里要特別指出,在類比過程中,既要講清它們的共同點,也要指出它們的不同之處,以培養學生用一分為二的辨證唯物主義的觀點看問題,能使學生更好地理解所學習的內容,在教學中起到舉一反三的好效果,類比的有效性才完全而真切地體現出來。
【參考文獻】
[1]湯服成,祝炳宏,喻平.中學數學解題思想方法[M].廣西師范大學出版社,2000.12
[2]稍齊昌.數學課的對比式教學粗探[J].數學教學通訊,1981(1)
【作者簡介】黃玉鳳,女,壯族,理學學士,崇左市天等縣高級中學教師,中學一級教師,研究方向:高中數學教學。
(責編 盧建龍)

