學生“角色轉換”在數學課堂中的落實

顧衛清

[摘 要] 以正弦函數圖象的教學為例，談學生“角色轉換”在數學課堂中是如何具體落實的，并與傳統的教學中學生的角色進行參照對比，尋覓適合學生角色的課堂教學.

[關鍵詞] 學生角色轉換；數學課堂；正弦函數圖象

課堂有三要素：教師、教材和學生，這三個要素誰是核心呢？中國傳統教育賦予教師“傳道、授業、解惑” 的任務，教師是教學活動的核心，學生處于服從的、被動的地位. 隨著新課改的深入，新的教育理念和教學模式要求適度打破這種僵化的師生關系，代之以靈活的、多樣化的角色擔當. 比如，讓學生做課堂活動的“主角”，教師成為其“配角”，甚至讓學生參與設計課堂目標和課堂活動等等. 我們看到，師生角色定位的翻轉帶來的是教學行為的巨大變革. 最近興起的微課、慕課、翻轉課堂等新形式的課堂研討活動，有力地促進了這種變革的進程. 但是，微課、慕課畢竟不是真正的課堂，把角色轉換的理念用之于實際教學，還有一個嘗試與整合的過程，其間必然地會有這樣那樣的不自然、不習慣甚至不情愿. 所以為了學生的發展考慮，我們做教師的必須有這樣的職業自覺：接受新理念，創造新業績.

下面就以筆者的親身體驗，談一談在課堂教學中如何適時地進行角色轉換，進而提高學生的活動效益并最終最大限度地促進學生的發展. 筆者選取的教學案例是《正弦函數的圖象》的教學.

讓學生充當提問者的角色

教學不是教師的“個人行為”，課堂更不是教師自我展示的“秀場”，學生的發展才是教學的立足點、出發點和終極追求. 因此，學生的主動參與是確保課堂效益的必然要求，學生應當是更積極、更有活力的因素. 如果學生能明確教學的目的、任務，自主地設計學習與探究的活動，則極有利于活動的主動、有序地展開，提高活動的效率.

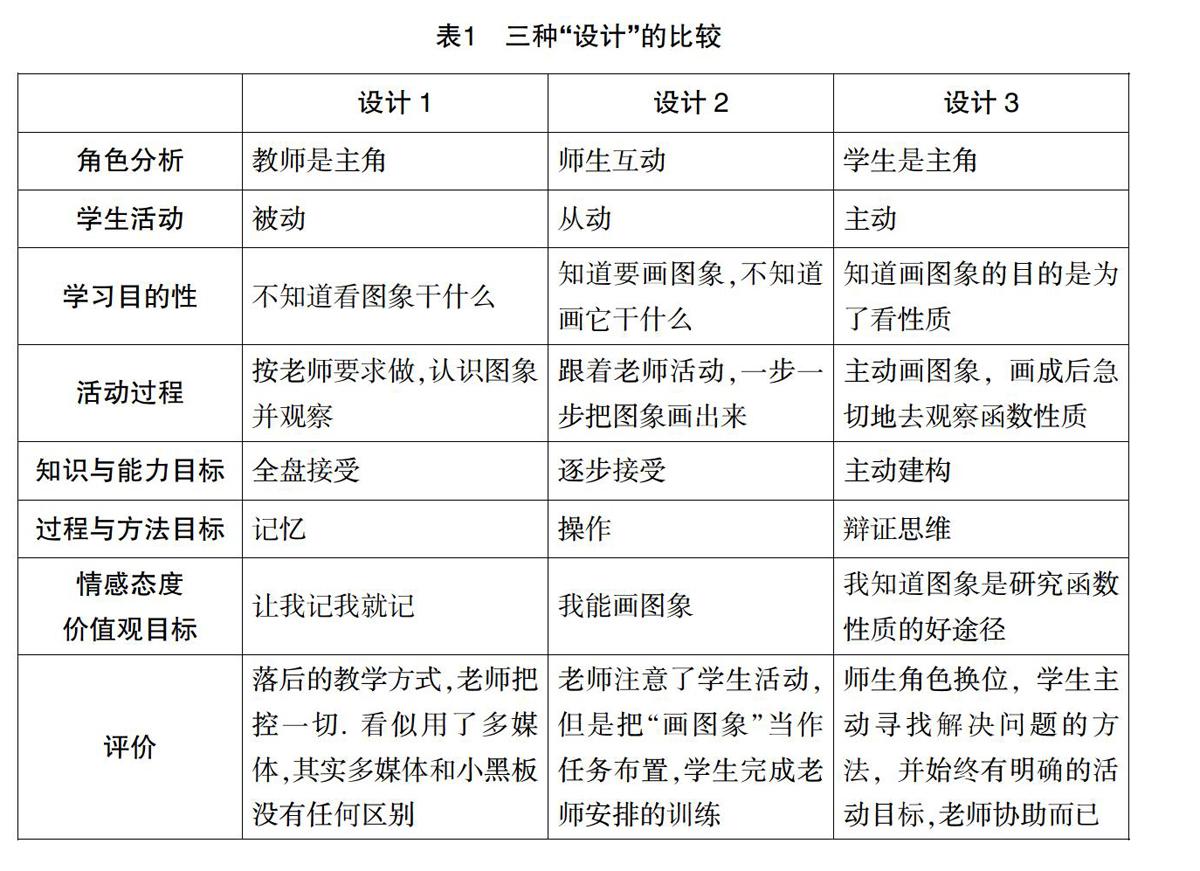
如“三角函數的圖象和性質”的第一課時“正弦函數圖象的畫法”，我們對下面的幾種“教學設計”做一番比較：

設計1 老師直接展示圖象（用小黑板或用多媒體），并告訴學生：這就是正弦函數的圖象. （學生認識它、觀察它）

設計2 老師出示這節課“正弦函數圖象的畫法”，然后布置學生活動：請畫出正弦函數的圖象. （學生設法畫圖象、再觀察體會）

設計3 有了正弦函數，我們就要研究函數的性質. 那么，怎樣研究正弦函數的性質呢？（學生先考慮：用什么手段研究函數性質呢？借鑒以前的研究冪、指數、對數函數的經驗，想到必須畫圖象，于是進入活動）

在設計1和設計2中，也存在著學生活動，但是活動是被動的、服從式的，在活動的過程中沒有明確的目的性因而就沒有創造性. 這樣的活動過后，學生獲得了一些記憶性知識或操作性技能，但是與“創新”基本沒有關系. 同時，學生的學習也并不輕松（他們不停地跟著老師的步調，完成老師提出的任務），因此在情感態度價值觀上沒有正面強化和提高.

設計3中，老師僅僅是拋出了一個話題.更值得注意的是，而且這個話題并不是這節課的課題. 因為這節課的課題是“正弦函數圖象的畫法”，老師的話題卻是“怎樣研究正弦函數的性質”. 學生在思考這個話題的時候，就會調用他們已有的認知體系或數學活動經驗，想到“通過圖象來研究函數的性質”. 這是從無到有的發現，他們把舊經驗應用于新情境，產生了一個創新思維成果.

從學生自己提出“怎樣研究函數的性質”，到發現“作函數的圖象”，雖然還沒有進入實質性的探索階段，但是他們的學習動機已經很強烈，創造的激情已經激發.所需要的就是鼓足勇氣，向著他們自己提出的目標進發了.

愛因斯坦曾說過：“提出問題比解決問題更重要”，《課程標準（修訂版）》也強調要培養學生的“問題意識”，其中重要的是發現問題的意識. 設計3可以說很好地涉及了這些意圖，是學生創新能力生長的溫床.

讓學生充當探路者的角色

學生有了“自己的問題”之后，在較高的求知欲驅動下，自然地進入了這節課內容的探究與發現——努力地去畫出正弦函數的圖象. 這時的學生位于發現的前夜，也許正是感覺上最為黑暗的時候.老師是不是要及時地為他們指引一條通向光明的道路呢？筆者認為不可以.

盡管學生在這時可能處于苦悶和彷徨之中，盡管他們中的大多數可能在新問題面前束手無策或者經歷一番拼殺后鎩羽而歸，但是這些痛苦的經歷也是他們成長過程中必須有的，是寶貴的財富. 就本節課而言，筆者放手讓學生沿著他們的思路前行.下面記錄的是學生接下來的活動過程：

怎樣畫函數的圖象呢？——只有描點法了，因為沒有已知的函數圖象可用.

列出哪些點呢？——當然是選特殊角，比如列出

（以前的經驗，描點一般不超過6個.）

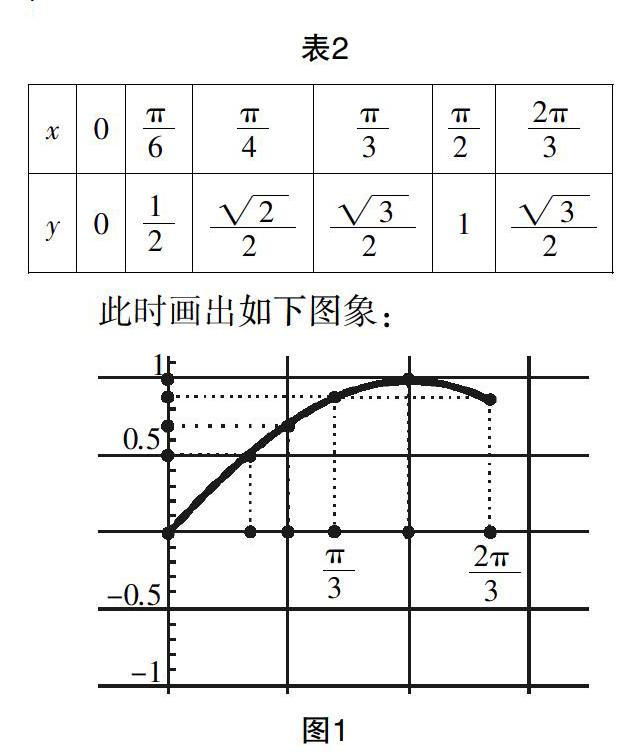
列出6個點后，發現毫無規律. 而且縱坐標不是特殊值，帶根號，有點討厭. 學生處于迷惘和苦悶之中，怎么辦？——再多列幾個點，嘗試嘗試吧（見表3）：

此時的圖象如圖2：

增加點的個數后，容易發現函數值重復了——思維敏捷的學生會聯想到sinx=sin（x+2π），于是想到利用這種“函數值重復”的性質，只需列出從0到2π的點就可以了.

列出從0到2π的一系列點以后，學生對于帶根號的縱坐標仍然比較苦惱.

（這時，老師主導作用就該發揮了）老師問學生：帶根號很可怕嗎？學生接受老師的引導：帶根號不是問題，近似計算就是了. 學生畫圖，老師等待.

老師再問：如果不想近似計算，是否有精確畫圖的方法？就此引出用單位圓中的三角函數線確定縱坐標.學生畫圖，老師充分等待.

讓學生充當成功者的角色

用兩種方法把圖畫完后，學生比較疲倦，心里也不是很舒服，畢竟那兩個作圖過程太煩瑣. 老師得啟發學生，有沒有稍微簡單的方法，簡明扼要地畫出正弦函數的圖象呢？學生思考或合作交流，再加上老師的參與，很樂意采用五點法作圖. 至此，畫圖工作宣告完成.

在這一教學案例中，我們來看看老師和學生的角色定位到底是什么（見表4）.

由此看到，學生始終站在舞臺的中心，提出問題的是他們，發現路子的是他們，具體落實的是他們，收獲成功的還是他們！老師僅僅是開了一個頭，在情感上給他們以鼓勵，完成最后的總結和肯定.

看看“設計3”中學生的狀態，再對比“設計1”和“設計2”，角色轉換極大地激發了學生學習的積極性，進一步提高了學生學習的思維品質，同時學生主動參與課堂活動愿望強烈，抓住了課堂的生長點，使之煥發無窮的活力，也為培養新時代的創新人才提供土壤. 這就是筆者有興趣在這里進行深入探討的原因所在.

老師不要搶奪學生的風頭，更不要擔心所謂“不起眼”的成功會使得學生得意忘形. 經由復雜曲折的過程而取得預期的或意外的成功，對學生而言是非常享受的. 老師只需默默地陪伴著學生，最好的教育是陪伴. 讓學生充分表現，讓他們享受成功的喜悅，就像享受陽光、空氣一樣. 學生在享受成功過程中，也能讓周圍的學生一起高興，分享成功帶來的歡樂，增進師生、生生之間的情誼.

讓學生充當評價者的角色

回顧與反思往往是老師完成的，但是實際上如果讓學生成為自覺的反思者，將是他們走向成熟的必不可少的步驟. 大的方面講，“多有只知責人不知反省的人的種族. 禍哉，禍哉！”（魯迅語），小的方面看，“人區別于動物的根本一點在于人會反思”（蘇格拉底語），由此可知反思對于一個人的重要意義.

就以本節課而言，我們可以提供給學生反思的地方很多.

（1）畫圖象中的描點也不是單純的技能，是伴隨著策略選擇的，思維在其中起著靈魂的作用.

（2）數可以精確地描繪現實，但是實際操作中無理數的精確度是有限的，這時的圖形反而是精確無誤的.華羅庚說過：“數缺形時少直觀，形缺數時難入微”，在這里出現了相反的情況. 所以，看問題應當有辯證的觀點.

（3）解決一個新問題，只有宏觀思路是不夠的，還要有切實可行的措施. 其間可能會有艱難困苦，會有山重水復，只要我們有明確的目標和堅強的意志，就能堅定不移、持之不懈，最后達到柳暗花明的境地.

結束語

學生的角色轉換源于教師教育觀、學生觀、教材觀的調整，是生本主義理念的具體實現. 問題是，在這樣的教學過程中，老師充當了什么角色呢？播種者、引領者和陪伴者，他們是學生的可靠伙伴，也是學生心靈的安慰者. 理念轉換出成效，角色轉換促教學.“學生角色”在數學課堂上的轉換，實現了教師與學生特性的有效展示，實現了教學活動效能的有效提升. 這是我們需要面對的新課題，值得繼續探討.