高中數學知識的實際應用解析

王麗云

[摘 要] 數學知識的實際應用，是深化數學知識理解的重要途徑，北師大版的高中數學教材的編排注重數學知識的實際應用. 數學知識的實際應用對于學生而言實際上存在兩個互逆的過程：一方面教材提供的實例及其解決，是學生利用已學知識進行問題解決的過程，而學生可以在對不同實例的歸納當中獲得此類問題解決的一般思路；另一方面，學生在形成解決思路之后，又可以利用這一思路去尋找新的與數學知識相關的問題.在這個互逆的過程中，學生的解題能力會得到增強，數學素養可以得到提升. 文章以“解三角形的實際應用”為例，闡述了教學實踐中的有關思考.

[關鍵詞] 高中數學；數學知識；實際應用；數學抽象；數學建模

課程改革以來，一個教學理念得到了普遍的重視，那就是通過數學知識的實際應用來促進學生對知識的理解. 根據這一要求，不同版本的教材在編排的時候也出現了實際應用的相關章節，這使得一線教師在教學的時候更加有章可循. 但在實際教學中我們經常看到這樣的現象：教師將這些實際應用類的章節教學當成簡單的數學知識的延伸，只將其作為一種應用類的例題來講解，而忽視了其本該具有的“實際應用”的價值，這樣的教學筆者認為不符合實際應用教學理念的初衷，問題的突破關鍵在于，怎樣才能體現出這種實際應用性呢？對此問題，筆者結合自己的教學經驗進行了持續的探究. 現以北師大版高三數學必修五教材中的“解三角形的實際應用舉例”為例，談談筆者的看法.

高中數學教學中數學知識實際應用的理解

實際應用，從字面來看，應當是數學知識在實際情形中的應用，這樣的理解實際上也是眾多一線教師的直覺性理解. 但作為教學理念的運用，筆者以為僅僅有此實際應用還是不夠的，還需要做出進一步的解讀.

結合高中數學教學的要求與實踐，筆者以為數學知識的實際應用應當有著這樣的幾個層次的認識：

第一層次：實際應用首先是將數學學習的觸角伸向生活

實際應用的本義，是將數學知識運用到實際生活中，這首先是學生學習視角的變化，通常情況下學生只關注抽象條件下自身解題能力的培養，并不關注具體實際情境中數學知識的應用. 但因為其在傳統評價方式中并不影響學生的應試能力，因而并不影響應試的效果. 但筆者發現另一種情形，即學生在實際應用中如果能夠得心應手，那在解決陌生的數學問題的時候，往往能夠表現出更為強大的能力. 這對當前數學教學是一個重要的啟發，即可以突破講了才會、不講不會的痼疾. 因此，當學習的觸角伸向生活，是可以有效提升學生的問題解決能力的.

第二層次：實際應用強調的是學生的數學抽象能力培養

但數學知識的實際應用，又不僅僅是數學與生活實際的簡單聯系，而應當是學生在面對實際問題時表現出來的數學抽象的能力，畢竟，實際事物呈現在學生面前的往往不是一個純粹的數學問題，而是由實際應用包裹著的數學問題，因此學生需要將實際情形進行數學抽象. 數學抽象的過程，是一個運用已有數學知識解構實際問題的過程，在此過程中學生的方向選擇是否正確，所用的數學工具是否恰當，影響著數學抽象的結果. 更重要的是，在此過程中學生會不斷地出錯，這個出錯過程往往是學生雜亂思維走向清晰的過程，很有助于學生把握數學知識的應用.

第三層次：實際應用需要學生的數學建模作為支撐

實際應用類的問題有一個顯著特征，就是需要數學模型的參與. 實際上上述第二點數學抽象的結果之一，就是建立恰當的數學模型，可以這么說，建立數學模型并分析數學模型，才是數學知識實際應用最為核心的環節. 因此，實際應用需要高度關注數學模型的建立.

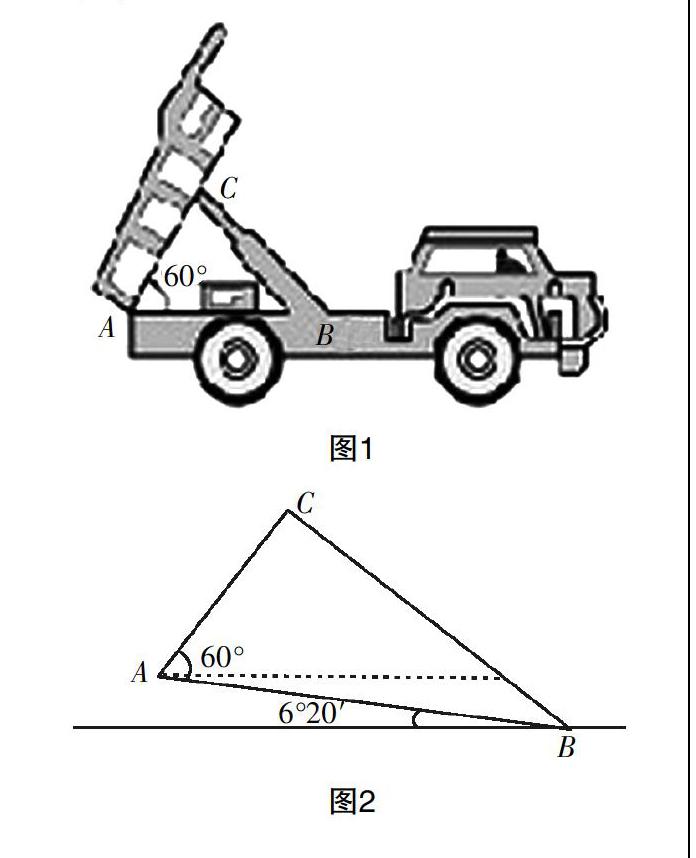
結合上面三個層次的理解，來看“解三角形的實際應用舉例”中有引入自動卸貨汽車液壓機構的例子：首先，三角形知識與汽車液壓結構相聯系，就是數學思維向實際延伸的具體方式之一；其次，在此基礎上，學生需要將實際的汽車液壓實物抽象成三角形圖形（如圖1），并基于已知與未知關系建立帶有數量關系的三角形模型（如圖2），然后利用余弦定理求解（具體略）. 在這個實例當中，遵循著全部以上三層理解，是一個典型的三角形知識在實際應用中的例子.

課堂教學如何凸顯數學知識的實際應用性

實際上，并不是所有的數學知識都需要強調實際應用性，忽視了這一點，在數學教學中就會陷入實際應用的“亂花”，常常容易“迷人眼”，反而容易忽視需要重視實際應用的數學知識的教學意義. 那么，在高中數學教學中如何凸顯數學知識的實際應用性呢？結合“解三角形的實際應用舉例”的教學，筆者做了這樣的兩點思考：

第一，實際應用的例子從哪里來

綜合“解三角形的實際應用舉例”這節教材的內容可以發現，實際應用的例子更多地體現出三角形知識在生活中的原型，比如說汽車液壓裝置，比如說煙囪高度的測量，比如說后面習題中的山頂高度的測定等，這是符合教材編寫的思路的. 根據三角形知識中已知與未知的關系，去倒推生活中可能存在的三角形實例，并將之改造成符合本部分知識學習需要的實際應用類問題，就可以成為一個關于三角形的實際應用專題. 事實上筆者還對本課題中的“舉例”一詞進行了關注，通常來看，舉例一般是幾個例子的同時列舉，并不具有關聯特征，從這個角度講，本知識的教學還有拓展的余地，當然這也是符合當下新課程標準所強調的“用教材教”的理念的.

第二，實際應用可以引導學生進行探究性應用

讓學生從所學的知識出發，去思考現實生活中可能與此相關的例子，那會出現什么樣的情形？在“解三角形的實際應用舉例”一課的教學中，筆者曾經做過這樣的嘗試，在解決了第一個例題之后，筆者沒有繼續教材上的實例，而是提出“在我們的生活中，還有哪些是可以利用三角形知識來解的實際應用類的問題呢？”顯然，這個問題具有相當的開放性，學生此時的思維過程是怎樣的，是筆者重點研究的內容. 研究表明，學生此時的思維包括這樣的幾個過程：首先，重現三角形的相關知識，尤其會回憶此知識學習過程中遇到的一些純粹的數學問題；然后學生會根據這些數學問題，去思考生活中有沒有基本相同的實際問題，但此種思考往往沒有多少結果；再然后，學生會回憶三角形中的具體知識，如正弦定理、余弦定理的證明過程等，這個時候往往會想到一些簡單的與三角相關的實際問題. 如，學生想到的是測旗桿的高度（可能與之前的知識積累有關），測河流的寬度等.

那么此時有沒有可能形成突破呢？筆者幾經努力，發現還是有辦法的，但這需要教師做一些前置性的工作，這就是在一開始的例題教學過程中，要突出強化數學抽象與數學建模的過程，讓學生深刻認識到實際應用的過程，就是數學知識形象化的過程，也是實際事物抽象化的過程，只要這個過程熟練，那學生在由三角知識向生活回歸的時候，就會順利得多.

實際應用應當成為教學設計與實施的重點

不是每一個數學知識都要通過實際應用來加強認知的，但一旦選擇了實際應用這一教學思路，那就需要認真對待，要將實際應用的原汁原味體現出來. 從這個思路來講，實際應用應當成為教師教學設計與實施的關注重點，要努力落到實處.

在“解三角形的實際應用舉例”一課的教學中，筆者致力于上述強調的重點：數學抽象與數學建模.努力走好實際應用的歸納與演繹兩步：歸納即通過教材或其他資料的實例，探究實際應用類的問題解決思路，從中認識到數學抽象與數學建模存在的價值，這個過程主要由學生在解決后的反思來完成，因為唯有反思，才能將內隱的解題過程顯性化，才能將相對雜亂的數學思維清晰化. 而演繹則是在學生反思的基礎之上，通過對已有的實際應用類的問題進行歸納，發現其規律之后再到生活中尋找相應知識可能存在的情境. 從歸納到演繹，是學生學習能力的一種提升，是數學視野從數學視域向生活視域的一種延伸，是數學知識從抽象走向形象，再從形象走向抽象過程的經歷，對于高中學生來說，是一種不可多得的學習經歷.

總之，實際應用類的知識應用，要注重學生思維過程中歸納與演繹兩個互逆的思維過程，并在此過程中強化數學抽象與數學建模，這樣才能真正提升學生的問題解決能力，才能真正提升學生的數學素養.