數形結合思想在初中數學課堂的教學現狀分析與思考

徐松海

[摘 要] 數形結合思想是初中數學教學的重要內容之一，本文結合調查研究，分析了該思想在初中數學課堂的教學現狀及原因，并結合實踐給出教學建議.

[關鍵詞] 初中數學；數形結合；教學現狀；教學建議

數形結合不僅是一種數學問題的處理方法，更是一種常規的數學思想. 初中數學教學關注學生數形結合思想的培養，因為其有助于發展學生的問題解決能力，能促成學生對數學知識的理解，提升他們的綜合素養，那么，該思想的實際教學情況如何呢？以下是筆者的調研和思考.

初中數學課堂中數形結合思想

的教學現狀概述

針對數形結合思想在初中數學教學的具體情況，筆者以問卷調查和訪談的方式對此進行了調研，得出以下結果.

1. 教師層面的調查結果說明

（1）有相當一部分教師沒有充分意識到數形結合思想在初中數學教學中的重要意義，因此課堂上極不重視該思想的教學滲透.

（2）絕大部分教師只有在進行習題教學時，才會將數形結合思想作為一種解題方法進行使用，他們并不注重在新授課教學時幫助學生培養這一思想.

（3）有一部分初中教師已經認識到數形結合思想在學生記憶和理解某些數學知識難點時的優勢，并積極指導學生熟悉相應操作，促成學生學習效率的提升.

（4）初中數學教師在對學生進行方法教學時，對方法的選擇具有很強的靈活性：當某些問題既可以從代數角度進行處理又可以用幾何方法進行解決時，大部分教師為了有效拓展學生的思維，往往兩種方法都予以介紹；當然也有部分教師純粹從解題便捷的角度出發，引導學生以最簡單的方法來處理問題.

（5）初中數學教師大多能全面地領會數形結合思想的基本內涵，而且充分認識到數形結合思想的運用能幫助學生對問題進行簡潔化與具體化，進而優化問題.

2. 學生層面的調查結果說明

（1）學生雖然已經逐步形成運用數形結合思想來對數學知識進行理解和記憶的基本意識，但其實際運用能力還有待提升.

（2）絕大多數學生都有運用數形結合思想解決問題的意識，也有極少數學生這一方面的意識有待加強.

（3）學生對數形結合思想內涵的理解還比較片面和狹隘，絕大部分學生局限于“以形助數”這一方面的認識，即通過圖像來解決代數問題，而對該思想的另一方面“以數助形”，學生的認識尚有欠缺.

（4）在“以形助數”方面，學生作圖的規范性有待強化，在“以數助形”方面，學生從圖形中“尋找”數的能力要強于從圖形中“構造”數的能力.

基于教學現狀的思考

基于對教學現狀的調查分析，筆者有以下幾點想法.

1. 教師自身對該思想有著較為深刻而全面的認識，但是教學中卻略顯片面，主要原因有以下幾點：（1）作為數學理論的基礎性思想，數形結合幾乎滲透在初中數學的每一個階段，它作為一種隱形的存在，離散而瑣碎，沒有嚴格的體系化，學生也只能在教師零碎的教學中結合自己的運用逐步形成有關認識；（2）以人教版的數學教材為例，課本上的內容和知識點側重于“以形助數”的方法運用，而“以數助形”的出現頻率明顯偏低.

2. 教師雖然認識到數形結合思想在學生理解和內化數學知識中的重要性，但是很多時候依然將該思想定格為解題方法，在數學理論新授課時不予以方法上的引導，以致學生對該思想的運用思路較為單一，理解也比較狹隘.

3. 絕大多數學生重視“以形助數”的操作，忽視“以數助形”的方法運用，其原因有以下兩點：（1）“以形助數”將抽象的代數問題以具體而直觀的圖像進行呈現，為學生問題的理解和解決帶來很大便利，該方法的優勢提供給學生“形”優于“數”的假象，以致他們忽視“數”在計算和邏輯推理方面的強大作用，進而導致他們“以數助形”意識的淡薄；（2）在平常的練習過程中，“以形助數”的問題比“以數助形”的問題多，以致學生前一方面的能力在頻繁訓練中不斷提升，相反，后一方面的能力就有所欠缺.

4. 學生作圖不夠規范的原因在于他們平常的習慣不到位，“以數助形”能力發展不均衡，特別是學生由圖構造數的能力偏弱，關鍵在于這一能力對間接思維的要求較高，這些問題需要教師在教學中不斷地予以強調和指導，啟發學生做出調整，實現提升.

教學建議

結合調研中的問題發現和思考，筆者認為我們的教學要從以下幾個方面進行改進.

1. 隱形滲透和系統介紹相結合

作為一種思想教學和意識培養，潛移默化地進行滲透性教學是常規做法，但是考慮到初中生對方法的自我歸納能力不足，筆者認為在隱性滲透的同時，教師也要將數形結合思想進行顯化處理，對學生進行系統介紹，讓學生形成全面而深刻的認識.

例如在“一次函數”的教學過程中，筆者引導學生從特殊的一次函數圖像著手探究，最終形成對一般化的一次函數性質的認識. 此時，筆者并沒有讓學生停下發現的腳步，而是啟發學生進一步發掘函數圖像的特征，最終形成認識：對于兩個一次函數y=k1x+b1和y=k2x+b2，當k1=k2且b1≠b2時，兩條直線平行；反之，如果兩條直線平行，那么它們所對應的函數解析式必然存在k1=k2且b1≠b2 . 學生的認識不應該止步于此，筆者引導學生進行總結：前者屬于由“數”到“形”，后者屬于由“形”到“數”，它們屬于數形結合思想的兩個方面，由此讓學生對該思想的形成有更加全面的認識.

2. 在知識形成過程中滲透思想教學

教師不能局限于將數形結合思想運用于解題，而應該在新課教學中，引導學生在體驗知識的形成過程中，感悟該思想方法的存在，由此啟發學生利用這一思想來深化對規律和概念的理解.

例如，在學生已經學習過運用消元法處理二元一次方程組的問題之后，教材還安排學生結合一次函數來處理二元一次方程組的問題. 筆者在引導學生學習這一內容時，并沒有照本宣科，而是同時運用“數”與“形”的方法來幫助學生剖析方程解法的實質，讓學生明白：消元法屬于“數”的方法，從圖像的角度來理解它，其實就是兩個一次函數圖像的交點. 由此，學生從“數”和“形”兩個不同的側面深刻理解了方程組解法的實質. 如果教師能在新課教學中經常讓學生體驗知識的形成過程，感悟數形結合思想在其中的運用，那么這不僅有助于學生領會對應的知識，也有助于他們思想方法的培養.

3. 展示過程引導與培養學生的構造能力

針對學生“以數助形”能力的缺陷，教師在實際教學中要注重為學生展示從圖像中構造數的基本過程和相關方法，從而讓學生在模仿中對構造能力進行培養，最終促成他們數形結合思想的系統化培養.

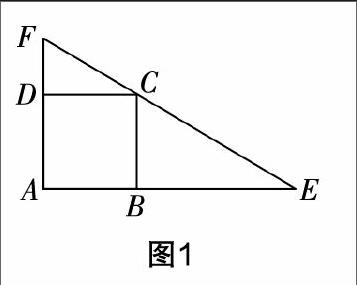
例如，如圖1，在正方形ABCD中，先過其頂點C畫一條直線，該直線與AB，AD的延長線的交點分別為點E和點F，求證：AF+AE≥4AB.

分析 這是一道典型的幾何問題，問題情境圍繞圖形來搭建，可用條件較少，筆者引導學生經過觀察和對比，啟發學生構建輔助線，然后通過面積相等這一等量關系，構建方程，將其轉變為“數”的問題，最終實現證明.

證明 （構建輔助線）連接AC，設AE=a，AF=b，AB=c，且根據△AEF的面積等于△ACF與△ACE的面積之和，再結合三角形的面積計算公式，有結論AE·AF=AF·CD+AE·BC；又由于正方形的四邊相等，即AB=CD=BC=c，所以有ab=（a+b）c. a，b可以看成是一元二次方程x2-（a+b）x+ab=0的兩根，因為Δ≥0，即（a+b）2-4ab≥0，所以（a+b）2≥4ab. 將ab=（a+b）c代入上式并化簡后得a+b≥4c，因此AF+AE≥4AB.

在上述問題的求解中，教師要引導學生關注從圖形來建構“數”的整個思維過程，要啟發學生思考“怎么做”和“為什么這么做”兩個問題. 化簡上述方程的過程中出現了ab=（a+b）c，這一等式同時出現兩數之和與兩數之積，因此教師要善于引導學生將其聯想到一元二次方程，同時結合待證明結論中兩數之和與某數值四倍的大小對比，根的判別式有關結論就會浮出水面，進而層層推進完成證明過程. 在問題處理過程中，教師不僅要啟發學生參與“數”的構造過程，更要和學生探討思路的來龍去脈，從而引導學生對過程與方法進行內化，提升他們“以數助形”的思維能力.