淺談初中數學教學中實驗滲透的有效性

董香鳳

[摘 要] 數學學習需要各種手段交替進行，需要嚴密的邏輯證明，需要感性的直觀認識，需要操作的實驗感知，需要巧妙的猜想歸納等. 在數學教學中滲透數學實驗，對于培養學生的數學學習興趣、提高學生的數學學習動手能力來說，都有益.

[關鍵詞] 初中數學；數學實驗；動手；直觀；頻率；統計

眾所周知，數學教學有很多呈現方式，特別是對于剛剛進入初中學習的學生而言，多元化的學習方式恰恰是最需要的. 從小學到初中，學生思維特征轉換尚未完全實現，學生可以接受一定的抽象數學，但又不能完全達到理解的地步. 大多數初中數學完成了從感性向不斷理性證明的過程，因此各種平面幾何的證明、二次函數的分析大大降低了學生數學學習的積極性. 筆者認為，需要在適當環節加入多元的學習手段，通過非形式化的手段、具象化的展示，將這種形式化的論證過程通過數學實驗加以滲透，以提高教學的有效性.

深化知識

很多數學核心概念都是經過上百年甚至更久的時間形成的，它不可能在短時間內讓學生迅速完全理解，并掌握它所有的內涵. 為了加快學生對這樣的核心概念的理解，筆者認為可以設計一些具備概念外延、表象的情境，來加深學生對相關數學概念的理解，進而感受概念.

案例 復習“函數”概念及其相關問題，多元復習設計，加強概念理解，提高問題解決能力.

函數概念是中學數學最重要的概念，是最核心的數學概念. 初中數學對函數的表述是以變量和變量的關系進行總結的，這種關系對于學生來說感受并不到位. 筆者對函數概念進行了重新設計，從三個層面層層遞進地推進對函數概念的認識，從而提高函數教學的有效性和深度.

設計1 （視頻實驗）用視頻展示如何將大米加工成各種各樣的食品，如面粉、糕點、面條、包子等.

設計意圖 函數關系最根本的體現是變量與變量之間的關系，如何讓學生首先從感性認識中體會這種變量與變量的關系呢？筆者設計的是利用數學視頻實驗將同樣的大米不斷地放入不同的加工機，產生各種不同的制成品. 學生容易理解這樣的生活情境，同時又心存疑惑：為什么要放這樣的視頻呢？這與今天要學習的函數知識有關系嗎？這一視頻實驗在向學生不斷滲透一個知識信號：任何函數都是以x（數）為自變量，經過不同的對應法則（加工機）得到不同的新的y（因變量）的一種對應關系.

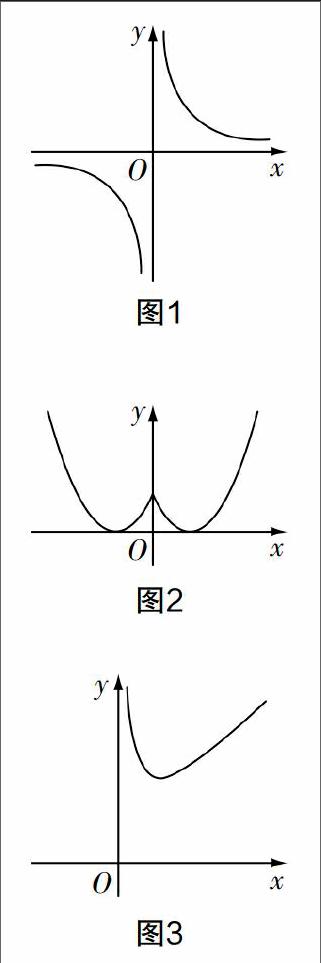
設計2 （圖形實驗）請學生在學案中繪制正確的函數圖像若干幅（如圖1、圖2、圖3）.

設計意圖 通過函數圖像“形”這一特點，利用學生在學案上繪制的函數圖像，課堂中直接利用幾何畫板將學生繪制的、有效的、有價值的函數圖像給以呈現. 筆者將這一設計稱之為教學中的圖形實驗，其意圖是通過函數圖像中“形”這一顯著特點，讓學生充分理解函數概念闡述的變量與變量之間的直接對應關系，即每一個自變量x對應唯一的一個因變量y. 在這一圖形實驗設計環節，有不少學生提供了有創新意義的函數圖形，比如圖3，學生畫了類似體育標記“耐克”的函數，這一圖像讓學生在學習函數的過程中體會到了其在生活中所具備的形態，讓數學學習根植于生活、運用于生活.

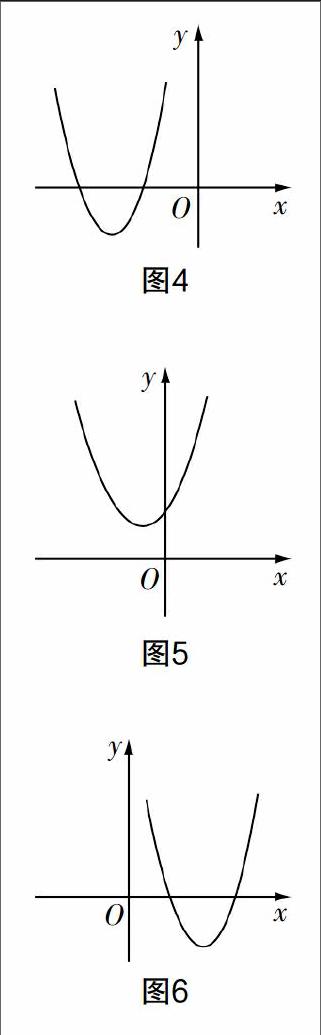
設計3 （動態試驗）利用現代信息技術教育手段，從動態變化中研究函數問題. 如研究二次函數相關問題：函數y=x2-2mx+8在-1≤x≤1的最小值為1，求m的值.

設計意圖 對于初中生而言，含有參量m的值讓學生對于問題的思考變得不太直觀，更因為自變量x受限于范圍-1≤x≤1，所以初中生普遍不能接受問題的含義. 筆者設計了動態試驗，利用幾何畫板中的參數功能，讓函數隨著參數m的變換而變化（圖4、圖5、圖6），從中可以清晰地看出在參數變換的過程中，其最小值并不完全由對稱軸處的值確定，這會與初中生腦海中“在頂點處取到最值”這一固有思維形成認知沖突. 可以請學生分析此函數問題為何要分類討論，有沒有與函數概念相悖，分類的依據是什么等，從而提高函數內容復習的深度和有效性.

不難發現，層層遞進的相關實驗操作，學生已經感受到了數學的可操作性，思考了知識的延續性、承接性，這對函數知識學習的深化起到了一定的復習效果. 從課程理念來說，這種一邊實驗一邊研究的方式，能讓學生體會到數學多元的學習途徑，能讓學生在嚴密邏輯推理的同時結合感性的實踐操作加深對知識的理解，提升復習的有效性.

理解概念

部分數學概念需要通過實驗去理解，比如八年級數學中隨機事件概率的定義. 概率是統計中的重要概念，其來源可以通過大量的數學實驗進行操作，即通過“頻率與機會”一課來學習概率的概念.

1. 教學設計

（1）為了讓學生充分理解隨機事件頻率值是一個隨著實驗次數而不同的、較穩定的值，所以課堂教學采取了大量的數學實驗操作來加強學生的理解.

（2）通過討論、思辨，使得學生理解頻率的穩定值即為概率，每一次實驗頻率值都不相同，但概率不隨實驗次數的改變而改變.

（3）（課后）與學生一起重做蒲豐投針問題，感受概率是頻率的穩定值這一重要特性.

2. 實驗操作

（1）教師選擇概率中的經典實驗：拋硬幣. 記拋出正面為上為事件A，將學生分成10個小組，每組中兩位學生負責拋硬幣，兩位負責記錄. 總次數分別為10次、20次、50次、100次、自定義次.

（2）請學生繪制表格，將拋出正面為上的次數分別記錄下來，計算出拋出正面為上的次數占總次數的百分比.

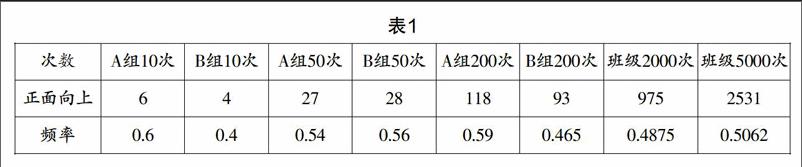
（3）請學生觀察：每組學生都有五組數據，有十個小組，共五十組數據. 數據分析從兩方面入手：一，各自小組內部的數據分析及頻率值變化；二，班級五十組數據的研究分析及頻率值變化，從數據中感受頻率值與實驗次數的關系（如表1）.

（4）從多次實驗，特別是大數據實驗的結果來看，我們都發現正面向上的頻率始終穩定在某一個常數左右，頻率值隨實驗次數的不同而不同，但是實驗次數越多，頻率值越趨向于某一個常數，這種直觀感受越明顯.

設計意圖 從概率的角度來說，概率論本身就是一門有關數學實驗的章節，筆者以經典的拋硬幣實驗為載體設計了本課相關的數學教學. 這一實驗所需設備簡單，可操作性強，并且通過多次實驗產生的數據可以產生新的思考，引發學生思考為什么實驗次數越多，正面向上頻率值越趨向于某一個常數. 從學生親自動手操作的實驗中，學生認識了頻率概念的意義：頻率并不是固定不變的常數，它與每一次實驗有關，一般來說，每次實驗所得到的頻率值不相同，但隨著實驗次數的增加，頻率值愈來愈穩定地趨向于某一個常數. 這樣的數學實驗能讓學生深刻理解頻率到底是一個什么樣的數學概念，后續可以進一步向學生介紹概率值的意義，以及各種有趣的數學實驗，如蒲豐投針問題等，讓數學實驗融入數學教學中，增強學生的數學學習興趣，提高學生數學概念的理解能力.

總之，數學實驗是數學教學有益的補充. 近年來，數學課程標準提出了讓學生學習數學更多元的學習手段的要求，其中有關數學實驗、數學探究性學習、信息技術在數學教學中的應用等，都是很好的嘗試和方向. 筆者認為，加強多形式、多維度的教學方式的使用，對于學生數學學習興趣的增加、主動性的增強都是有益的，更能從不同的角度加深對知識的理解，從而提高教學有效性.