四用幾何直觀，巧構空間觀念

楊俊娜

文章編號：1674-120X（2018）36-0061-02

摘 要：《義務教育數學課程標準（2011年版）》把幾何直觀和空間觀念這兩大核心概念融入數學思維的培養中，明確在小學階段數學教學中要重點培養學生幾何直觀的能力，建立發展學生的空間觀念，這在立體幾何的教學中表現得尤為明顯。學生此前已經掌握了平面幾何圖形的基本特征，但這僅僅是停留在直觀形象的認識，要進一步深入地研究立體幾何圖形，對于空間觀念相對薄弱的小學生來講還是存在一定的難度。因此，文章就以《認識長方體》為例來談談如何借助幾何直觀培養學生的空間觀念。

關鍵詞：小學數學;幾何直觀;空間觀念

中圖分類號：G623.5??文獻標識碼：A

幾何直觀是《義務教育數學課程標準（2011年版）》新增核心概念之一。其概念和作用被首次定義為：通過利用圖形的描述和分析問題，借助幾何直觀可以把比較復雜的數學問題變得簡單、明了、形象，并且有助于探索解決問題的思路和預測結果。因此，在小學階段數學的教學中發展幾何直觀顯得尤為重要。怎樣才能幫助小學生更好地建立空間觀念呢？筆者認為，可讓學生經歷想象、觀察、操作、驗證等過程，巧妙積淀空間觀念必備的思維品質與關鍵能力。下面就以《認識長方體》這課為例，談談筆者在教學實踐中的做法。

一、巧用幾何直觀，讓想象“飛”

想象，即在改造記憶表象的基礎上創造出新形象的一種心理活動。離開了想象，數學學習將會變得蒼白無力、困難重重。因此在課堂教學上有效激發學生的想象力是立體幾何教學中的重要內容之一。

例如，在教學《認識長方體》這節課時，教師先通過一張A4白紙帶領學生回顧長方形的基本特征，為新授內容中研究長方體的特征做好鋪墊。緊接著教師請學生們閉上雙眼，把這張紙想象在腦海里，然后再想象出若干張完全相同的紙，一張一張地重疊在一起，讓想象“飛”起來，讓若干張完全相同的紙重疊起來最后形成長方體。本環節通過幾何直觀里的想象因素來幫助學生感受長方體的形成過程，從而構建學生的空間概念。

通過想象一張紙到一包A4紙張的堆疊過程，讓學生插上想象的翅膀，經歷由平面圖形到立體圖形的形成過程，感受視覺上的沖擊。教師揭示課題后，緊接著讓學生展示課前搜集的長方體實物，找一找教室里常見的長方體物體，感受生活中的數學。目前許多教師在平時的課堂教學中傾向于用圖形來代替實物，這樣雖然在一定程度上可以節省備課時間，避免搜集物體的煩瑣，但筆者認為，簡單的幾何圖形是無法取代生活中的幾何實物的，一旦缺乏生活的感知，就很難幫助學生從已有的生活經驗中抽象出長方體的幾何圖形;只有經歷感知實物，再從中抽象出長方體幾何圖形的過程，才能讓學生體驗數學源于生活的道理，學會用生活的眼光來感受數學。

二、妙用幾何直觀，讓觀察“躍”

觀察是一種有目的、有計劃的知覺。小學階段的學生處于比較好動的階段，難以靜下心來思考問題，靜下來的時候也根本起不到觀察的效果，多半是在發呆。筆者認為，要想達到觀察的目的，就必須在此前明確要求，提出具體的任務，讓觀察跳“躍”起來，讓學生有目的地參與進一些教學活動。只有這樣，學生才能深入觀察，有事可做，才能達到良好的教學效果。

在《認識長方體》一課中，教師讓學生先通過自學的方式認識長方體的面、棱、頂點，同桌互相介紹然后匯報，最后用摸一摸的方式讓學生感受面、棱、頂點，利用觸覺來加強學生的認知。緊接著在探究長方體面、棱、頂點特征的時候就采用跳躍的觀察模式。即先提出以下要求。

（1）數一數長方體面、棱、頂點的數量分別是多少？不單單是用眼睛看，還要用嘴巴數，并且思考怎么數才能做到不重復、不遺漏，滲透有序的數學思想。

（2）用尺子量一量長方體的棱，哪些面完全相同，哪些棱長度相等？不單單是直覺上感受，還需動手操作進行驗證思考。

（3）完成書本第19頁的表格，并和同桌說一說你是怎么驗證的。討論自己的想法。

教師可以利用上面的表格讓學生自主探究，同時學生在自主學習時有明確的要求及研究目標，不再是靜靜地觀看，而是運用跳躍的觀察模式，從而建立高效課堂。這個知識點是本節課最重要的環節，學生對面、棱、頂點的直觀認識僅僅停留在數量的多少和大小等方面，本環節需要學生更深入地掌握面、棱、頂點的內在邏輯關系，全面掌握它們的特點。運用幾何直觀中跳躍觀察的因素，讓學生觀察自己準備的長方體實物，從教師給的要求入手，對照六大內容，觀察之余利用數一數、量一量、比一比、說一說等具體的活動，發現棱、面、頂點之間的關系。除此之外，學生活動結束后的匯報情況以及教師對學生的引導也制約著該重點和難點的突破。在學生匯報時，教師層層深入、步步設問，通過眼觀、手動、腦想、嘴說等各種感知覺的交錯配合來構建學生的相對空間觀念。學生充分感知有關長方體的空間觀念就比較容易形成。親身動手實踐、參與討論發言能讓學生經歷長方體圍成的過程，從而培養學生的空間觀念，提煉出概念的認知。

三、善用幾何直觀，讓操作“思”

隨著現代信息技術在教學中的廣泛運用，不少教師以課件演示來代替學生動手操作環節，這種過于依賴課件的傾向越來越嚴重，也存在教具資源缺失以致單靠教師一人展示的現象，這樣學生就失去了動手制作幾何模型的機會。對于空間觀念相對薄弱的小學生，這樣教學是行不通的，必須引導學生親自進行操作，讓學生動手拼一拼長方體框架模型。

比如，用12根小棒拼一拼長方體框架，本課中以四人小組為單位開展大比拼活動，同時教師提出思考要求：在拼之前根據長方體有12條棱這個特征先把小棒分分組，想想怎么拼才能又對又快？在規定時間內，請拼得最快的小組派代表跟大家分享下獲勝的秘訣。

學生匯報時有兩種分法： 一種分法是把長方體的12條棱分成3組，每一組相對的4條棱長度相等。另一種分法則是根據將相交于同一個頂點的三條棱分成一組，共4組。從而水到渠成地過渡到長方體的長、寬、高的概念。通過動手操作活動，學生動手、動口、動腦的能力都得到了鍛煉，多種分析器官共同參與活動，通過切身的體驗進一步理解了長方體棱的特征，清楚地看到了12條棱的關系，從而進一步抽象概括，思考對棱的分類，總結出棱長總和的計算方法。教師在教學中運用幾何直觀中的操作探究性實踐活動，能讓學生在活動中逐步感受、逐步領悟、逐步形成、逐步發展空間觀念。

練習是學生鞏固知識、運用知識的實踐活動，它不僅是教師教學的手段，而且還是促進學生智力發展和能力培養的重要手段。認識完長、寬、高之后，本節課的教學內容基本完成，筆者設計以下三道題來幫助學生對已學知識加以鞏固。

題一：已知廈門市鼓浪嶼水族館里需要配備一個底面和正面如圖1規格的長方體魚缸，請你說一說它的長、寬、高分別是多少？

題二：根據相交于一個頂點的三條棱想象出一個長方體（如圖2），并回答下列問題。

（1）長是（? ? ），寬是（? ? ），高是（? ? ）。

（2）左面是一個（? ? ）形，長是（? ? ），寬是（? ? ）。

（3）后面長是（? ? ），寬是（? ? ）。

（4）（? ? ）面和（? ? ）面的面積是84平方厘米。

（5）做這樣一個長方體框架需要多長的鐵絲？

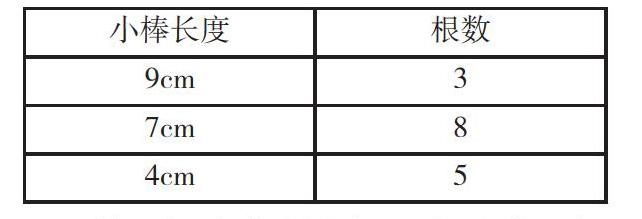
題三：下面是老師為同學們準備的小棒（有多余），試著用這些小棒和橡皮泥做一個長方體框架。

（1）相交于同一個頂點的三條棱? 分別長多少厘米？

（2）這個長方體框架的棱長總和是多少厘米？

并根據本節課的知識點設計了如下的練習。題一是已知長方體底面和正面的長和寬，需要學生根據長方體面的特征勾勒出長方體模型，從而明確長、寬、高的長度。題二是給出空間位置上的三條線段的長度，在認識完長方體棱的特征及根據安放的位置如何確定長、寬、高后，鞏固長、寬、高的定義，用逆向思維算出各面的長、寬各是多少，此外還滲透長方體的棱長總和計算方法。題三則是基于學生動手拼長方體框架，進一步鞏固本節課所學的全部內容。整個練習設計由易到難，體現了練習設計的針對性和層次性，起到了掌握重點、突破難點的作用，并進一步鞏固了學生的空間觀念。

四、精用幾何直觀，讓驗證“實”

正所謂實踐出真知，猜想驗證的方法在小學數學中是一種重要的數學思想。在本節課設計中，教師時刻注重驗證思想的滲透，讓驗證成為實實在在的看得見、摸得著的東西。

第一環節的想象從一張紙最終堆疊成一包A4紙張，成為一個長方體，讓學生睜大眼睛驗證變化后的結果，看似微不足道的細節，卻給學生留下一種求真務實的感覺。在探究長方體面、棱、頂點的特征，討論哪些面完全相同時，從長方體實物中可以直觀地看出相對的面完全相同，在設計的環節，教師可以追問“你是怎么驗證的？”進一步啟發學生進行思考及動手實踐驗證的思想。有的學生想出用重合法畫出來，有的則是用尺子量，發現量出長和寬數據相等之后，就可以斷定兩個長方形完全相同。當然，教師在這里就可以利用課件移動重合，讓學生一目了然地看到相對的兩個面完全相同。有了前面的驗證，在棱的特征方面學生就會自己動手驗證。

總之，幾何圖形是很抽象的，在課堂教學中，教師通過簡單的堆紙活動讓學生想象形到體的演變過程，用手摸感受長方體面、棱、頂點的直觀特征，用眼觀察加之雙手實踐驗證，掌握立體圖形各部分的特征，動手操作拼接長方體框架，最后總結出長方體的特征，從而破本節課的重點、難點。巧妙地借助幾何直觀進行教學，可以形象生動地展現問題的本質，有助于促進學生的數學理解，引領學生從直觀走向抽象，幫助學生建立幾何模型，構造學生的空間觀念。

參考文獻：

[1]劉心怡.初三學生“幾何直觀”現狀的調查研究[D].南京：南京師范大學，2014.

[2]李玉龍，朱維宗.小學初步空間觀念及其培養[J].現代中小學教育，2008（10）：47-49.

[3]梁春燕.趣味數學游戲[M].廣州：華南理工大學出版社，1994.

[4]王林生.在“猜想——驗證”中發展探究能力——以“梯形的面積”教學為例[J].基礎教育論壇，2015（12）：36.