初中數學教學中數形結合思想的滲透

林慧

【摘要】在數學教學過程中，有機結合數與形，可以有效轉換抽象思維，并形成形象式思維，進而在不同程度上揭露數學教學本質，大大降低數學知識學習難度，有助于提高學生學習水平.

【關鍵詞】初中數學；數形結合；思想滲透

初中數學教學過程中，應用數學結合思想就是結合數學教學中的各項知識內容，讓學生可以將形象與抽象思維有效結合，從而實施兩者轉化性學習，讓抽象概念能夠轉變成較為具體化的圖形.為了可以對數形結合思想更加清晰地了解，本文研究了函數中與應用題中“數學結合”思想的差異，希望能夠提高初中學生的數學學習能力.

一、初中數學函數中滲透“數形結合”思想

數形結合具有眾多優勢，它能夠讓抽象的函數與直觀圖形之間實現雙向聯系，達到化抽象為形象的目的.在初中數學知識學習中，由于一般二次函數問題是十分抽象的，在學習中，由于這部分知識學起來有些困難，學生不愿意學習與二次函數有關的數學題.由于二次函數有其自身特征，因此，同函數圖形之間有著密切的聯系，初中生只要是在直角坐標系下，就能夠找到函數關鍵之處，在定位下來做圖形，這樣問題分析也就會變得更加形象化.從理論層面上分析，在y=ax2+bx+c二次函數中，參數a決定著開口方向，c決定了與y軸的交點，而a和b共同決定了二次函數圖形的對稱性.因此，若是在學習二次函數過程中使用數形融合的思想，就能夠妥善幫助學生處理這一實際問題.如，已知（-1，y1），（-3，y2），（2，y3）在二次函數y=3x2+6x+2圖像中，對y1，y2，y3的大小關系進行判斷.分析：此題是對二次函數大小進行判斷，若是初中生不知如何運用數形結合思想，就肯定會在二次函數中將每一個點的x值代入，

然后在將y值求出，這樣計算的話，不但計算量非常大，而且學生還可能會在計算中出現錯誤.但若是學生能夠運用數形結合思想做出來y=3x2+6x+2圖形，就能夠對y1，y2，y3之間大小關系進行對比.如右圖所示為y=3x2+6x+2簡圖.

二、運用數形結合思想可以簡化應用題學習

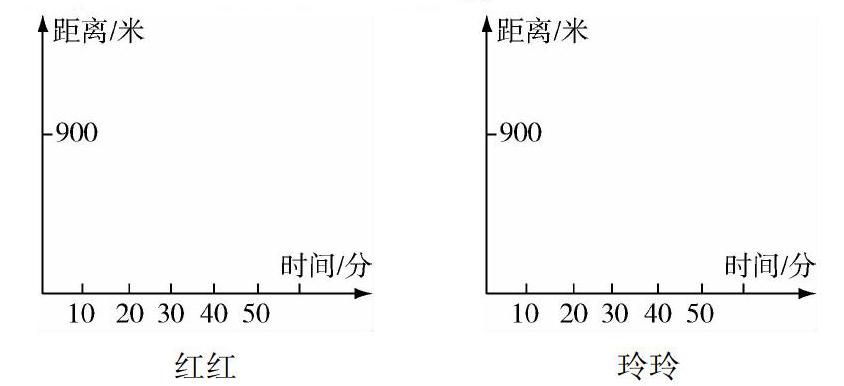
在初中數學知識學習中，不可避免要學習到應用題知識，并且在初中時期的應用題是十分有難度的，很多初中生計算半天也很難計算出準確答案.如，在“一元一次方程”學習中，教學者應帶領學習者閱讀應用題題目，從已知條件中得到題目中已給的條件，并分析每個要素間的關系.同時，在學習中能夠采用坐標系的方式來將函數圖像畫出來，在對函數圖像分析中，學生能夠快速地、有效地得出最終結果，從而簡化了整道應用題.如，紅紅與玲玲相約一同出去游玩，早上八點兩人一同出發，走了30分鐘后遇到一片綠草地，此草地距離家有900 m，紅紅玩了一段時間之后就不想玩了，便保持之前的速度趕回家了，玲玲在草地玩了15分鐘之后也走回家了，回到家后共花了20分鐘.結合這一段描述，可以在下面的平面直角坐標系中準確描述出紅紅與玲玲離家時間和距離的關系嗎？

紅紅

玲玲

對于這種類型的數學習題在初中數學知識學習中經常遇見，也是一類較為基礎型的數學習題.若是這種類型習題出現后，教學者引導學習者從日常生活中入手，并運用數學結合思想妥善解決這一問題.其中，結合題目中給出的信息，可選擇x，y兩個未知數表示距離以及時間，并表示好二者之間的關系.這樣一來，在不斷練習中，不但能夠加強學生對數軸知識的認識，而且也可以為學生日后學習這種類型的知識打下堅實基礎.

三、在數學概念學習中數形結合思想的有效應用

在數學知識學習過程中，數學概念是一項基礎的知識，對于引導學生深入學習數學知識有著很大的影響.在初中數學概念教學過程中，數形結合思想的應用，可以促使學生對數學概念知識更加有效地了解.在數學知識學習中，有很多概念都是抽象的，加大了進行課程教學活動的難度.數學教師可利用圖形方式講解這些知識，提高初中學生整體上掌握數學概念的能力.如，在引導學生對對稱軸知識學習中，教師能夠在對折某個圖形中，而后引導學生對直線兩邊圖形特征進行觀察，在數學教師對折后重疊了圖形，直線兩邊圖形也可以完全重合.教學者在帶領學生觀察和分析的前提下，引導學習者主動思考，并講出折疊之后圖形的特征，然后講出對稱軸的概念，使學生能夠輕松的、容易的掌握這節數學知識.

四、結 語

在初中數學課程教學過程中，應用數形結合思想有利于實現有效結合理論知識以及圖像表達，從而實現有效融合知識引導與思維培養，教師能夠根據學生認知特征，對數學結合思想巧妙的、形象的應用，確保學生可以對解答數學習題技巧更好地掌握，進而可以對數學知識更加輕松的學習，形成一定的數學思維.

【參考文獻】

[1]侯招琴.數形結合思想在高中數學教學中的有效運用[J].吉林教育，2017（31）：80.

[2]茅春娟.初中數學教學中數形結合思想的實踐探析[J].文理導航（中旬），2017（8）：28.