注重知識的形成過程,引導學生“學會學習”
王桓
【摘要】本文通過反思筆者自身公開課的處理方法——從平面向量和空間向量知識的聯系性出發,用類比的方法引導學生進行學習,輔助信息技術突破難點,得出“注重知識的形成過程,創設有效問題,引導學生學會學習”的有效方法。
【關鍵詞】類比 幾何畫板 學會學習
【中圖分類號】G633.6 【文獻標識碼】A 【文章編號】2095-3089(2018)14-0127-01
2017年12月14日,我參加了我校第十一屆“同題開課”活動,教授的課題是人教A版2—2中的第三章第一節《空間向量及其加減運算》,通過這次公開課,我經過深刻反思,認為數學概念的教學應該從以下幾方面來著手教學:
一、強調概念的本質,抓住知識的聯系性,引導學生在“類比”中形成概念
《普通高中數學課程標準》明確提出:強調本質,注意適度形式化。形式化是數學的基本特征之一。在數學教學中,學習形式化的表達是一項基本要求,但是不能只限于形式化的表達,要強調對數學本質的認識,否則會將生動活潑的數學思維活動淹沒在形式化的海洋里。
在本節課的教學中,我積極分析學生的基本情況,我校是太原市普通高中,學生雖然學過平面向量的知識,但是,已經過去了一個學期,學生應該是忘得差不多了,有必要重新復習后,再把相關概念進行推廣。因此,整節課的教學,通過導入——基本概念——特殊向量——向量關系——向量的加減——向量加法的運算律的推進過程,每一個環節都采用知識結構圖的類比形式,復習平面向量的知識后,抓住向量概念的關鍵——大小和方向,來引導學生進行空間向量知識的學習。
首先,在引入環節,我采取了向量的應用——位移的實例引入法,用下面兩個例子進行導入。既貼近學生生活,又能使學生身臨其境,體會到空間向量的存在意義和研究必要。
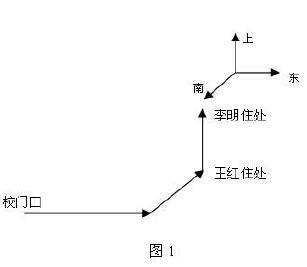
實例1:王紅從學校大門口出發,向北行走100m,再向東行走200m, 到達住處,如何用數學的方法刻畫王紅從學校回到家的位移?
實例2:李明從學校大門口出發,向北行走100m,再向東行走200m,最后上電梯15m到達住處,如何刻畫王紅從學校回到家的位移?
這兩個具體的實例,既貼近學生生活,又能使學生身臨其境,體會到空間向量的存在意義和研究必要。同時,我用PPT進行演示(如圖1),學生非常自然地進入這節課,同時對空間向量引入的必要性有了清晰的認識。
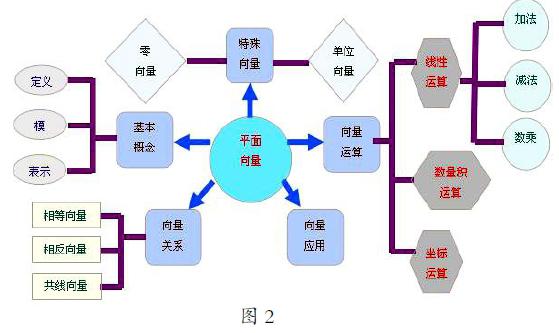
其次,在復習環節,我采用了知識結構圖(如圖2)的形式來引導學生進行復習。通過知識結構圖,引導學生將知識進行整合建構,同時有利于對接下來新一章知識整體結構的認識,幫助學生在運用類比方法進行研究的過程中,認真思考,仔細體會,形成概念,進而認識概念的本質,主動地對知識進行建構重組,在體驗過程中對知識進行升華認識。
二、巧妙運用信息技術,引導學生在體驗中“學會學習”
高中數學課程應提倡利用信息技術來呈現以往教學中難以呈現的課程內容,在保證筆算訓練的前提下,盡可能使用科學型計算器、各種數學教育技術平臺,加強數學教學與信息技術的結合,鼓勵學生運用計算機、計算器等進行探索和發現。
幾何畫板是專門的數學軟件,工具豐富,直觀明了,在這節課的重點內容——空間向量加法運算法則推導和運算律的驗證過程中,我采用了幾何畫板來演示。
首先,在三角形法則和平行四邊形法則的推導過程中,“為什么可以對向量進行任意平移”成為難點,兩個所在直線不共面的向量經過平移,實現了“首尾相接”和“起點相同”,轉化成平面向量的運算問題,從而使學生感受到空間向量中的三角形法則和平行四邊形法則。對于多個向量的加法,學生很容易就解決。
通過這一演示過程,學生通過自我體驗,清晰地認識到了“空間向量的加法法則”,實現了知識的自然過渡和有效遷移,極大地提高了課堂效率,為后續內容的學習奠定了良好的思維基礎,轉化劃歸思想在學生頭腦中形成了烙印。
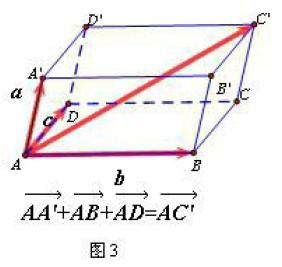
其次,對于“所在直線不共面的三個向量的運算”,我繼續引導學生類比平面向量的平行四邊形法則,用平行六面體法則進行遷移應用(如圖3),同時,為下一步進行空間向量的加法結合律奠定了基礎。
通過親身體驗,學生感受到了從二維平面向三維空間的順利遷移,為后續空間向量在立體幾何中的應用奠定了思維基礎。可見,在教學中,我們引導學生在探究過程中,充分運用現代媒體技術輔助教學,可以起到事半功倍的作用,促進學生思維上的飛躍,為后續的學習奠定基礎,同時,有利于學生對知識結構的理解,對知識進行重新建構,對思維能力進行整合提升,有利于發展學生的六種基本的數學思維能力。
《中國學生發展的核心素養》中明確提出:學生必須具有“學會學習”的核心素養,具體分為三個層面:樂學善學,善于反思,信息能力。作為教師,我們設計教學時,應該以學生的基礎為出發點,設計必要的環節,注重知識的形成過程,輔助必要的信息技術平臺,從創設情境的導入到有效的小結,都需要我們設置可以激發學生興趣,促進學生反思,引起學生進行信息處理的問題,引導學生在體驗中成長,在經歷中提升,最后達到對知識的本質的認識,在快樂中提升思想,增強提出問題、分析問題和解決問題的能力,為進一步的學習和工作提供必要的知識準備和能力基礎,真正做到“授之于漁”。

