中學數學教學中有效運用數形結合思想方法的研究

尚影

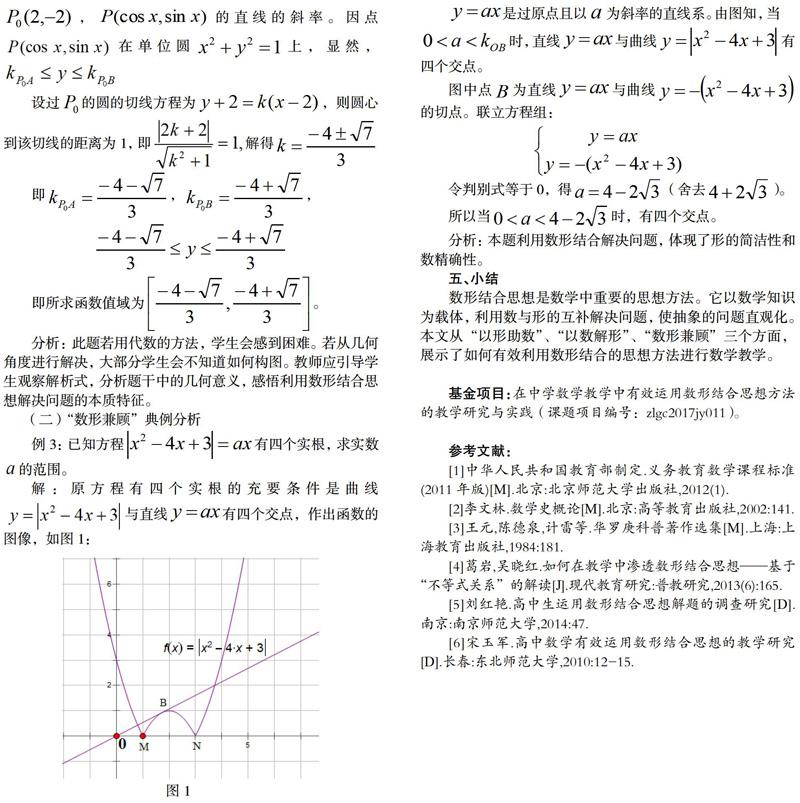
摘 要 中學數學內容包括兩個主要方面：數學知識和數學思想方法。在近年的新課程改革中，數學思想方法的教學已被日趨重視。恩格斯曾說：“數學是關于客觀世界數量關系和空間形式的科學”。教師在數學教學中應有效利用數形結合的思想方法，以提升學生的解題技巧，真正提高學生解題能力，并指導學生學會運用數形結合思想方法去解決生活中的實際問題。

關鍵詞 數學教學；數形結合；有效運用

中圖分類號：G632 文獻標識碼：A 文章編號：1002-7661（2018）08-0252-02

一、研究背景

數學思想方法作為數學學習的核心，它滲透于數學內容之中。新課標規定：“課程內容的呈現不僅要包含有數學結果，也要有數學結果形成的過程及其所蘊涵的數學思想方法”。很多國家都注重數學思想方法的教學，如：英國的“Cokcroft報告”對數學思想方法的教學提出明確要求，要讓學生通過學習數學，會用數學的觀點理解世界，并形成量化意識。

中學生運用數形結合思想方法時存在以下問題：

（一）想不到運用數形結合思想解題；

（二）運用數形結合思想解題時，數與形的轉換經常遇到困難；

（三）運用數形結合思想解題時，書寫不夠規范。除此之外，解題時還存在作圖不當；數與形進行非等價置換等問題。

二、數形結合思想方法概念

學術界對“數形結合”的解釋各有不同，下面是幾種常見的說法：

（一）張同君在《中學數學解題研究》中，認為數形結合是在問題解決過程中，將數量關系和空間形式進行結合，揭示問題的深層結構，從而達到順利解題的目的；……