向量在高中數學解題中的應用

徐有彪

摘要：數學課程作為高中教育的主干課程，一直是學生學習的難點，特別是在數學解題中，不少學生存在解題思路不暢、解題方法不對的現象，這除了和基本知識點掌握得不牢靠有關外，也和學生在數學學習中未能做到融會貫通有關。向量是一種既有大小，也有方向的量，具有數形結合的特點，不僅是高中數學的重要知識點，在學生其他問題的解題中也有著獨特的應用價值。本文基于此，從數列問題、三角函數、平面幾何、立體幾何四個角度探討了向量的解題應用。

關鍵詞：高中數學;向量;解題應用

向量是高中數學課程的重要教學內容，也是高中數學解決問題的常用工具。向量最早出現于物理學中，多用來表示速度、位移、力等，英國科學家牛頓首次將向量和有向線段聯系起來，為向量的數學應用鋪平了道路。18世紀末，挪威數學家威賽爾通過坐標平面上的點來表示復數a+bi，并借助具有幾何意義的復數運算來定義向量運算，向量正式進入數學領域。在高中數學教學中，教師要重視向量的解題應用，以此作為提升學生解題能力的有效方式。

一、數列問題中的解題應用

三、平面幾何中的解題應用

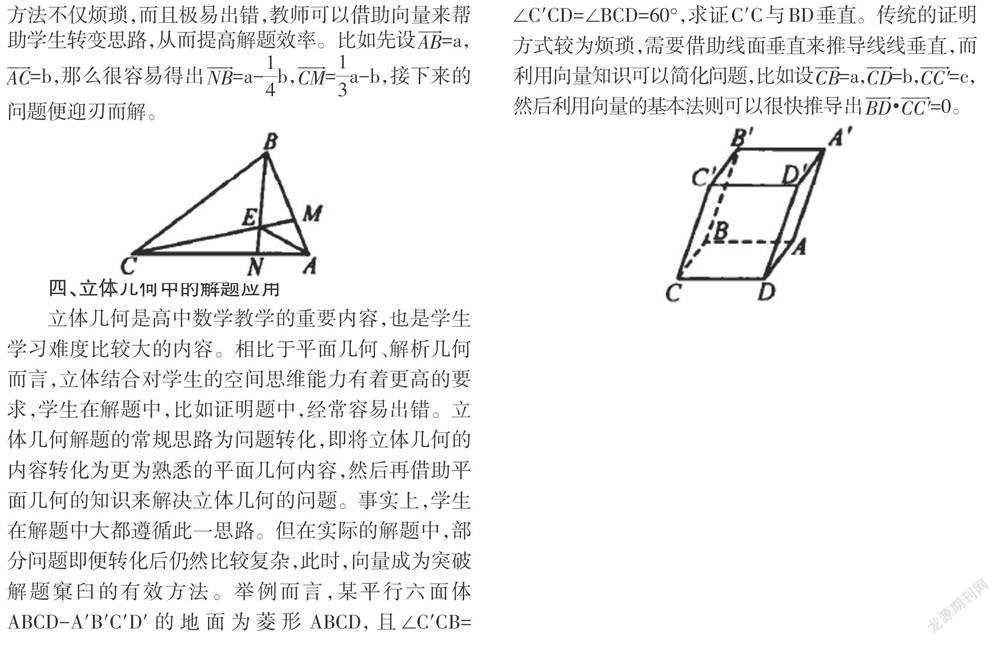
向量具有數形結合的特點，借助向量，不僅可以將枯燥抽象的代數問題轉變為直觀清晰的幾何圖形，也能將幾何問題中的煩瑣求證轉變為相對簡單的代數計算，從而實現化繁為簡的目標。就以平面幾何解題為例，不少平面幾何問題難以借助常規的解法求出，此時，教師可以引導學生嘗試著從向量的角度切人，將平面幾何問題轉化為向量問題，然后再利用向量的基本運算求解，降低題目的復雜性以及解題難度。舉例而言，已知某AABC，其中AM：AB=1：3，AN：AC=1：4，CN和BN相交于點E，若AB=m，AC=n，且∠BAC=60°，請求出AE的長度。本題涉及的知識點相對較多，傳統的解題

五、結語

向量作為高中數學的重要知識點，是學生數學解題的利器。高中數學中的向量兼有代數形式和幾何形式雙重特征，學生利用其代數形式來解決幾何問題，不僅可以提高學生的解題效率，在幫助學生串聯數學知識點中也有很好的效果。

（責編：侯芳）