數形結合思想在初中數學解題中的應用

呂惠

【摘 要】數學思想是數學知識的靈魂和精髓，其中一種常見的數學思想便是“數形結合”。函數作為初等數學中一個基礎而核心的概念，是初中教學的重難點，函數本身是很抽象的概念。引導學生運用數形結合的思想方法，把函數問題中抽象的數量關系轉化為具體圖像，把復雜的函數圖像轉化為簡單的數量關系，最后求解，就可以化抽象為具象，從而鍛煉學生解題的能力，事半功倍。

【關鍵詞】數形結合;函數;初中數學

【中圖分類號】G633.6? 【文獻標識碼】A? 【文章編號】1671-8437（2019）28-0121-02

著名數學家華羅庚曾說：“數缺形時少直觀，形少數時難入微;數形結合百般好，隔離分家萬事休”。數形結合思想是指將數與形結合起來分析、整理、解決數學問題的一種思想方法，在理解數學概念以及解題過程中都有廣泛應用[1]。數形結合思想貫穿整個中學乃至大學的數學學習中，因此，教師在中學教學中向學生展示數形結合思想的妙用，進而培養學生注重數學思想的意識是十分有意義的[2]。下文以蘇科版初中函數問題為例，展示數形結合思想在其中的運用。

1? ?數形結合理解函數

函數是中學教學中的重難點，是研究物理世界變化的一個模型，是整個數學體系中的重要思想，函數的內涵和外延都是極為抽象的。如何讓學生盡快理解、掌握和應用函數是教師應該研究的課題。

概念學習是函數學習中的第一步，其重要性顯而易見，如果學不懂概念，后面的學習便寸步難行。很多學生在學習概念時，采用強行記憶的方法，而不注重理解，這樣無疑對后續的學習造成巨大的困難。如果教師在函數概念的教學中，借助圖像的變化，讓學生先擁有圖像的直觀印象，再引入相關的符號以及變量來解釋函數概念。那么學生會容易接受許多。

以蘇科版教材為例，采用以下練習引入函數概念。

例1 向平靜的湖面投一石子，便會形成以落水點為圓心的一系列同心圓。①在這個變化過程中，有哪些變量？②若面積用S，半徑用R表示，則S和R的關系是什么？

解析：從圖像中得出S是關于R的函數。可以看到S和R是一一對應的，S隨R的變化而變化，從而引出函數概念，對R的每一個值，都有S中的值與之對應，那么S是R的函數，準確定義：一般的，在一個變化過程中，如果有兩個變量x和y，并且對x的每一個確定的值，y都有唯一確定的值與其對應，那么就把x稱為自變量，把y稱為因變量，y是x的函數。借助圖像，教師可以將函數概念中的符號和數量關系形象化，從而使定義更加直觀清晰。如果用傳統語言描述，則難以達到這么清晰的效果。學習函數概念后，對后續的一次函數，二次函數，反比函數，三角函數等的學習，也應該注意對概念的理解，學生能根據具體解析式畫出圖像，才是真正理解了函數的概念[3]。

2?  數形結合解決函數的應用

2.1? 解決函數概念的應用

在解決函數概念的應用問題時，運用以形解數的方法，將數量關系式轉換為圖像，解題更加簡單明了。

例2 鄂州市化工材料經銷公司購進一種化工原料若干千克，價格為每千克30元。物價部門規定其銷售單價不高于每千克60元，不低于每千克30元。經市場調查發現：日銷售量y（千克）是銷售單價x（元）的一次函數，且當x=60時，y=80;x=50時，y=100。在銷售過程中，每天還要支付其他費用450元。①求出y與x的函數關系式，并寫出自變量x的取值范圍。②求該公司銷售該原料日獲利w（元）與銷售單價x（元）之間的函數關系式。③當銷售單價為多少元時該公司日獲利最大？最大獲利是多少元？

解析：①將y與x的一次函數關系式寫出來，設為y=kx+b，把x與y的兩對值代入求解，得出k和b的值。②根據利潤=單價×銷售量，解出二次函數。③根據第二問的函數圖像求最大值，根據函數圖像觀察，最高點即是最大值，用代數計算算出圖像的最高點，體會圖像的最高點與最大值的對應。

從這道題，學生理解了如何從數量關系求出函數的解析式，理解了變量和函數的概念并與函數圖像相對應;第3小問以數解形，用代數計算，求解圖像，學生體會到數與形的相互轉化。充分體現數形結合思想的應用。

2.2? 解決函數性質的應用

在學習函數概念后，緊接著就是學習函數的性質，只有掌握了一個函數的性質，才能在解題過程中靈活運用函數，而在初等函數的學習中，學生往往感覺性質太多，記不住，容易混淆，真正的原因其實是學生沒有理解記憶，當記憶的越多，就會混亂以至遺忘，在解題過程中也就無法靈活運用。在教學過程中，教師應該強調讓學生將函數性質與圖像結合進行理解記憶。在運用函數性質解題時，大部分可以借助代數進行解答，但是多數學生往往覺得難以理解，運算量大，那么，通過畫出函數圖像，就可以將性質直觀化，從圖像中找到答案，則會簡便很多。如二次函數的對稱性質：對稱軸左邊，圖像從左到右下降，函數值隨自變量增加而減少;對稱軸右邊，圖像從左到右上升，函數值隨自變量增加而增加;頂點是拐點。學生在記憶增減性質時，應理解圖像的趨勢與性質的對應，而不用只記住性質的文字描述。

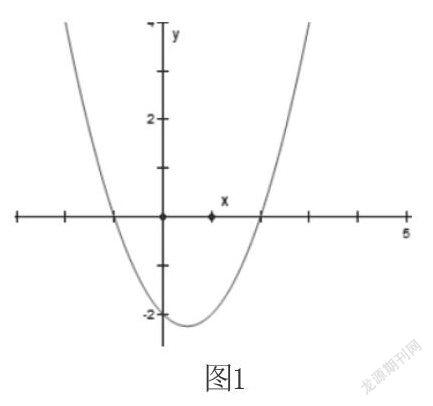
例3 求函數f（x）=x2-x-2的零點。

解析：首先學生要理解函數的零點其實是函數圖像與x軸的交點，那么只需要畫出函數即可。

從圖1中可以清楚地看到問題的解，如果直接將零點轉化為對應方程的根，不夠直觀，學生也理解困難，采用圖像即可幫助學生理解零點與圖像交點在x軸上的對應關系，進一步理解方程與函數圖像的對應關系。從這道題，學生理解到函數的零點是函數與x軸的交點，更進一步，引出函數與直線的交點，再推出兩個函數的交點。

如已知方程|x2+3x+1|=m有2個根，求實數m的取值范圍。

解析：二元一次方程的根可以轉化為二次函數與直線y=m的交點，將兩個函數的圖像畫出來，觀察他們的交點即可。觀察圖像即可得出答案，m=0以及m的值大于頂點時，有兩個交點。將方程左邊化簡（x+1.5）2-1.25，求得頂點縱坐標為1.25。故m≥1.25，或m=0。如果不畫出函數圖像，學生可能會想到分類討論的方法，但是根據圖像，只需求出特定值就行，簡便了計算，也加深了學生對函數的理解。

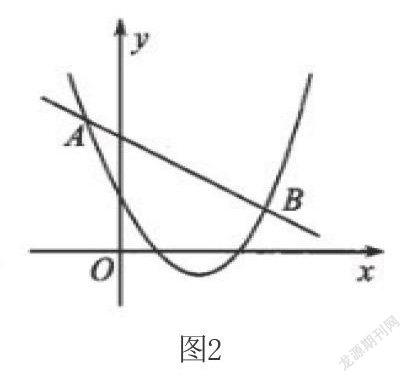
例4 已知二次函數y1=ax2+bx+c與一次函數y2=kx+m，（k≠0）的圖像交于A（-2，6）和B（8，3），則能使y1

解析：直接畫出大概的函數圖像（如圖2），即可解題。

在解決這類函數題時，充分應用數形結合思想，幫助學生進一步理解函數的性質，提高學生對函數性質理解和掌握的準確度。

2.3? 解決數學模型的應用

建立數學模型是一種重要的能力，在初中數學的教學過程中，運用數形結合的方法讓學生通過建立數學模型體會理論知識在實際問題中的應用，增加數學解題的趣味性，調動學生解決問題的好奇心，進而讓學生期待數學學習。因此，數形結合的思想方法是十分重要的。

如拋物線y=2x2+8x+k與y軸交于點C（0，6），動點P在該拋物線上當三角形POC是以OC為底的等腰三角形時，求

點P。

解析：在求解這類題時，應該根據已知條件，畫出拋物線的圖像，從而建立數學模型。首先根據點C在拋物線上求得k，然后設點P（x，y），過OC中點作y軸的垂線，由OD=3，求出P的縱坐標為3，由拋物線的解析式，求出P點的橫坐標為4±。

這道題在解題時充分展示了數形結合的思想，依據解析式畫出拋物線圖像，建立了拋物線的數學模型，再把拋物線的圖像與等腰三角形的性質相結合，從而找到解題的思路。在這類習題中利用數形結合思想，使題目更加直觀，學生也能更加理解函數知識的運用。

數形結合是數學學習中重要的思想，不僅在函數中舉足輕重，在代數、幾何中也發揮著重要作用。“數”與“形”的結合，包含了數學整個的學習內容以及研究過程。數形結合的思想不僅為學生解題提供了便利，更為學生的探究學習指出了方向，是數學學習過程中的重要方法[5]。初中數學的教學應該注重對數形結合等數學思想的培養，讓學生能夠靈活運用數學思想對初等數學進行深入的探究，培養學生的科研意識，為學生后續的學習之路打下基礎。

【參考文獻】

[1]雷紅，楊文.數形結合思想在初中數學解題中的應用——以初中函數問題為例[J].福建中學數學，2019（2）.

[2]王詩琳.數形結合思想在高中數學解題中的應用教育[J].才智，2019（3）.

[3]張發啟.數形結合思想在初中數學教學中的應用研究[J].課程教育研究，2019（4）.

[4]羅惠庭.數形結合思想在初中數學解題教學中的滲透策略[J].中學數學研究（華南師范大學版），2018（20）.