淺談初中數學教學中變式教學的有效運用

葉陽浩

摘 要 在初中數學教學中，教師為了能加深學生對數學知識的理解和認識，全面提高教學組織成效，應積極探索變式教學在數學教學中的應用，發揮變式教學的作用對學生實施有效的數學教學指導。本文從初中數學《全等三角形的判定》習題課程教學入手，對變式教學的有效應用進行了探究，僅供參考。

關鍵詞 初中教育;數學教學;變式教學;《全等三角形的判定》

中圖分類號：G32? 文獻標識碼：A?????? 文章編號：1002-7661（2019）09-0105-02

初中階段變式數學教學活動的開展對于學生數學綜合能力的培養產生著至關重要的影響，教師在全面推進數學教學改革的過程中積極探索變式教學方法的合理化應用，能在不同的數學形式變化下加深學生對相關知識和技能的理解，使學生能形成更加透徹的感知，鞏固學生數學綜合學習效果，確保初中階段學生的數學綜合素質能得到理想化的培養。在本次研究實踐中，將《全等三角形的判定》習題課作為對象，對變式訓練在初中數學教學中的應用進行了系統的探究，希望能為教師開展教學改革活動提供有價值的參考，推動初中數學教學改革實現深化發展，為學生數學綜合學習能力的培養創造良好的條件。

一、例題引導，回顧知識點

為了能在教學活動中有效組織開展習題課教學活動，教師在應用變式訓練教學的過程中應該先對全等三角形方面的知識點進行分析，借助例題教學引導學生回顧全等三角形的概念和性質等，確保學生能在學習環節加深對相關知識點的理解，做好習題訓練準備工作，增強習題教學組織效果。

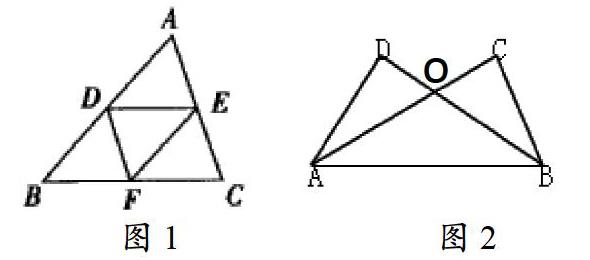
例題1：如圖1所示，已知△ADE≌△DBF，并且DE∥BF，DF∥AC，那么對應的邊為_____，對應角為_______。

例題2：如圖2所示，有△ABC≌△BAD，點A、B為對應頂點，點C、D為對應頂點，此時如果存在AB=6cm，BD=7cm，AD=4cm，那么你能計算出BC的長嗎？

通過合理實施例題訓練，教師引導學生對全等三角形的概念和性質進行回顧，應用這方面的知識對問題進行處理，加深學生對知識點的理解，對學生實施積極有效的訓練。在學生完成對例題內容的處理后，教師可以適當的要求學生對簡單的變式題目進行處理，確保能形成對全等三角形方面知識的系統化感知。

變式題1：如圖2所示，有△AOD≌△DBOC，點A、B為對應頂點，點C、D為對應頂點，此時如果存在AB=6cm，BD=7cm，AD=4cm，那么你能計算出AC的長嗎？

在借助例題引導對學生實施反復訓練后，學生能從不同的角度對這方面的知識進行分析，對于學生參與全等三角形判斷方面的鞏固訓練產生著重要的影響，能輔助學生對全等三角形判斷數學內容進行更加系統的探索，增強教學組織成效。

二、鞏固訓練，深化學生認識

初中數學教師把握學生在《全等三角形的判定》習題課中的具體表現開展教學活動，在學生能回顧前期所學知識有效對全等三角形判定方面簡單的數學問題進行處理后，教師要按照教學指導活動的現實需求，對學生實施鞏固訓練，讓學生能接觸更多的全等三角形判定方面知識內容，在鞏固學生知識掌握能力的基礎上，確保學生經過學習和訓練能合理的對這方面遇到的問題進行處理，有效促進初中階段的學生數學綜合素質得到理想化的培養。

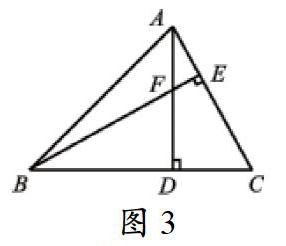
鞏固訓練題1：如圖3所示，已知在△ABC中∠ABC=45°，中F是高AD與BE的交點，并且CD=4，那么請計算線段DF的長度。

在這一層次的鞏固訓練中，教師引導學生回憶對本問題進行處理會應用哪些知識點，然后要求學生結合自己的理解對變式訓練題進行處理。

變式題2：如圖3所示，已知△ABC中，其中F是高AD與BE的交點，如果BF=AC，請計算∠ABC的度數。

教師要求學生對訓練題和變式題進行系統分析，然后思考和總結在已知一條邊和一個角的情況下對兩個三角形全等進行判定方面的主要問題處理思路有哪些。學生在對知識點進行回顧的基礎上能加深對這部分知識的理解，并且還能思考在已知兩條邊、已知兩個角時對三角形全等的判定方法，數學習題課程中知識鞏固的效果顯著提高。

在學生能基本對習題內容進行處理后，教師在鞏固訓練環節，可以提出更加復雜的習題訓練內容，幫助學生進行更加系統的學習和訓練，優化初中數學習題課程教學質量。

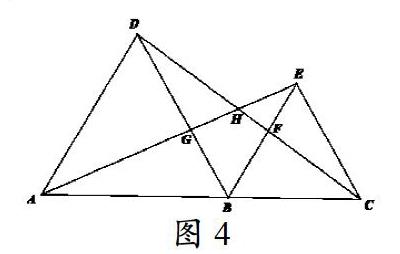
鞏固訓練題2：如圖4所示，已知點A、點B、點C共同在一條直線上，現在如果分別以AB、BC為邊在AC同側作兩個等邊三角形，分別為△ABD、△BCE，并且AE與BD相交，交點為點G，DC與BE相交，交點為點F。求證：AE=DC，BF=BG。

在指導學生對這一問題進行處理后，教師讓學生分析解決這一問題采用了什么方法，重點培養學生解決問題的能力。與此同時，教師把握學生的情況，適當組織學生參與變式訓練，深化學生的思想認識。

三、拓展探究，培養解題能力

根據“鞏固訓練題2”習題教學和變式訓練教學，教師就可以設置如下所示訓練項目，確保學生能使用相同的思路進行拓展探究，促進學生解決數學問題能力的合理化培養。

拓展訓練題1：如圖5所示，已知在等腰直角△ABC內有一點D，且∠CAD=∠CBD=15°，點E為AD延長線上的一點，且CE=CA。

（1）求證：DE是∠BDC的平分線;

（2）如果點M在DE上，且DC=DM，求證：ME=BD。

數學習題課中的拓展訓練實際上也屬于深層次變式訓練的內容，通過拓展訓練能使學生更好的把握數學知識點之間的聯系，在對數學知識點進行整合應用的基礎上實現對問題的有效處理，確保能進一步增強數學教學效果，為學生未來深入探究數學知識奠定基礎。

四、結語

在全面推進初中階段數學教學改革的過程中，按照先進教學思想和教學理念的指導探索教學改革措施，對初中階段的學生實施變式訓練教學指導，能循序漸進的改善教學現狀，增強初中數學教學活動的綜合效能，真正發揮出變式訓練的作用，達到預期教學效果，為學生更加深入系統的探究數學知識做出積極有效的指引。

參考文獻：

[1]黃亞奇.以“變”促教，引領高效教學——例析初中數學變式訓練的實施策略[J].數學教學通訊，2019（05）：68-69.

[2]孫壽春.變式教學在初中數學教學中的應用研究[J].數學教學通訊，2019（05）：70-72.