以“問”導學 以“問”促“學”
貴仁毅
【摘要】長期以來,教師“重教輕學”的教學觀念根深蒂固,造成了教師滿堂講,卻忽略了學生的感受和真正需求的教學現狀。問題導學教學法是要求教師在教學過程中,從“問題”中來,到“問題”中去,以“問題”引導學生學習,以“問題”促進學生學習的教學方法。它真正落實以生為本的理念,是發展學生核心素養的有效途徑。
【關鍵詞】問題導學;初中數學教學;運用
美國當代著名數學家哈爾莫斯說過:“問題是數學的心臟。”[1]20世紀80年代,美國首先確立“問題解決”作為中學數學教學核心。從此,“問題解決”受到世界各國中學數學教育的高度重視,“問題解決”逐步成為教師培養學生解題能力、自控能力和應用數學知識能力的有效途徑。問題導學教學法是指教師在課堂教學中以問題為載體,通過引導、啟發學生解決問題,達到以促進學生“學習”為根本目的的教學方法[2]。它要求教師在教學過程中,從“問題”中來到“問題”中去,以“問題”引導學生學習,以“問題”促進學生學習。本文將論述問題導學教學法在初中數學教學中的運用。
一、創設貼近生活的“問題”情境,激發學生的學習興趣
法國著名思想家、教育學家盧梭說過:“問題不在于教他各種學問,而在于培養他有愛好學問的興趣,而且在這種興趣充分增長起來的時候,教他以研究學問的方法。”在日常生活中,人們總是喜歡去認識、研究、探索自己感興趣的事物,這是人類的心理、思維慣性,是人類的共同點。中學生也是如此。因此,教師在教學過程中要努力創設貼近生活的“問題”情境,激發學生的學習興趣,激發學生主動探索的欲望,讓數學課堂教學收到事半功倍的效果。
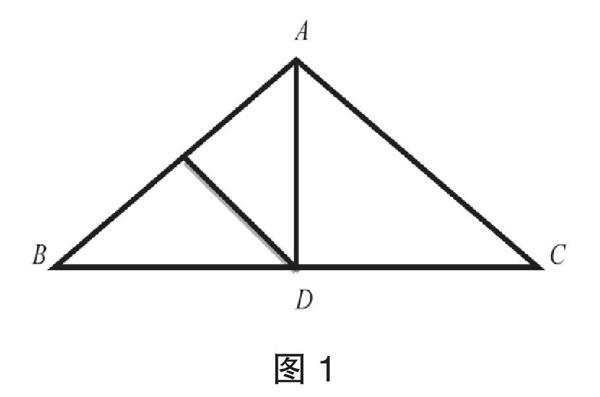
例如,“等腰三角形”是軸對稱特性內涵的直觀體現,等腰三角形相關性質為研究邊與角的聯系與轉化提供了理論依據。因此,在教學這一重要內容時,教師可以在導入階段利用多媒體播放云南特色民居、大理白族民居、傣族民居、上海世博會場館的圖片,創設貼近生活的“問題”情境,在激起學生學習興趣的同時,讓學生體會等腰三角形在生活中的應用。然后提出問題:“如圖1,云南的特色民居中,大多數房子的頂木框架是一個等腰三角形,要搭建等腰三角形ABC,已知AB=AC,立柱AD丄BC,BC=6,∠BAC=120°,求∠B的度數和BC的長度。”最后,教師進一步講解等腰三角形的腰、底邊、頂角和底角等知識。
創設貼近學生認知特點的問題,不僅讓學生對所學知識點感興趣,而且強化了學生對等腰三角形“三線合一”定理的認識,體現了“具體—抽象—具體”的思維過程,提高了課堂教學的效率。
二、構建“思辨”問題,引導學生進行深度思考
數學教學的目的之一就是教學生進行思考,提高學生的思維能力。因此,教師在數學教學過程中要培養學生的好奇心,調動學生情感、意志、毅力等非智力因素,讓學生進行邏輯思維訓練,引導學生進行深度思考。
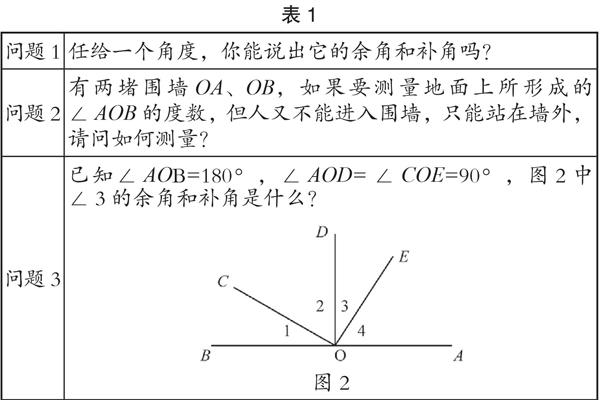
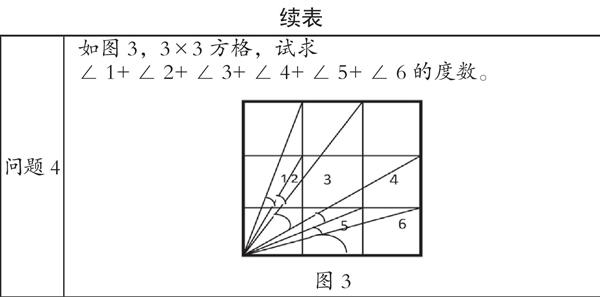
例如在學習“余角和補角”這一內容時,教師可以設計一系列的“思辨”問題,引導學生進行深度思考,激發學生的探究欲望。
通過構建“思辨”問題,激發學生的挑戰意識,將學生的思考引向更深層次,為學生進一步辨析數學概念,理解數學概念打下思維基礎。
三、設計系列“問題串”,促進學生邏輯思維、推理能力的發展
數學知識之間是普遍存在聯系的,教師要運用聯系的觀點幫助學生學習、理解數學知識,探索知識之間內在的聯系,促進學生邏輯思維、推理能力的發展,從而提高學生的學習效率。
例如在學習“方程和方程組解法”這一內容時,教師可以設計如下“問題串”。
四、開辟方法“問題”,啟迪學生感情,突破重點與難點
數學教學由數學知識教學和數學思想方法兩個方面有機組成。數學思想方法是數學中所蘊含的一般規律,是數學的靈魂。因此,在數學教學過程中,教師要重視方法教學,潛移默化地引導學生進行感悟和學習,在教會學生“怎么做”的同時,更要教會學生思考的方法。
例如在學習“相似判定和性質”時,教師可以給學生設計如下問題,讓學生進行思考,突破學習的重點與難點。如圖4所示,D是△ABC的BC邊上的點,BD∶DC=2∶1,E是AD的中點,連接BE并延長交AC于F,求BE∶EF的值。
問題導學教學法是一種可以培養學生學習興趣,教會學生思考的教學模式。教師在數學課堂教學過程中可以設計一系列的問題,引導學生進行學習與探索,鍛煉學生的思維,讓學生從“問題”中來,到“問題”中去,從而達到提高學生數學核心素養的目的。
【參考文獻】
(美)保羅·哈爾莫斯.我要作數學家[M].南昌:江西教育出版社,1999.
黃河清.中學數學“問題導學”教學策略[M].北京:中國林業出版社,2008.

