一節優質決賽課的欣賞與思考

李定平

【摘要】優質課決賽是同一課題《兩角差的余弦公式》，對優勝者的教學過程進行了介紹與評述，基于數學學科核心素養下對本課教學內容所蘊含的育人教育價值提出了不同的教學設計，即“問題引領，自主建構”的“問題串”教學設計，在問題解決的過程中發展學生的核心素養。

【關鍵詞】優質決賽課;教學設計;問題串

佛山市順德區高中數優質課決賽是兩位老師執教同一課題《兩角差的余弦公式》，筆者有幸聽了他們的課，其中，碧桂園學校國際課程熊曉敏老師的課讓筆者很有感想，下面分享筆者的心得，以饗同行。

一、流程簡單，卻憾動人

熊老師的課沒有挖掘什么教材內涵，也沒有補充什么綜合題、高考題，教學流程非常簡潔，效果卻非常好，教學過程如下：

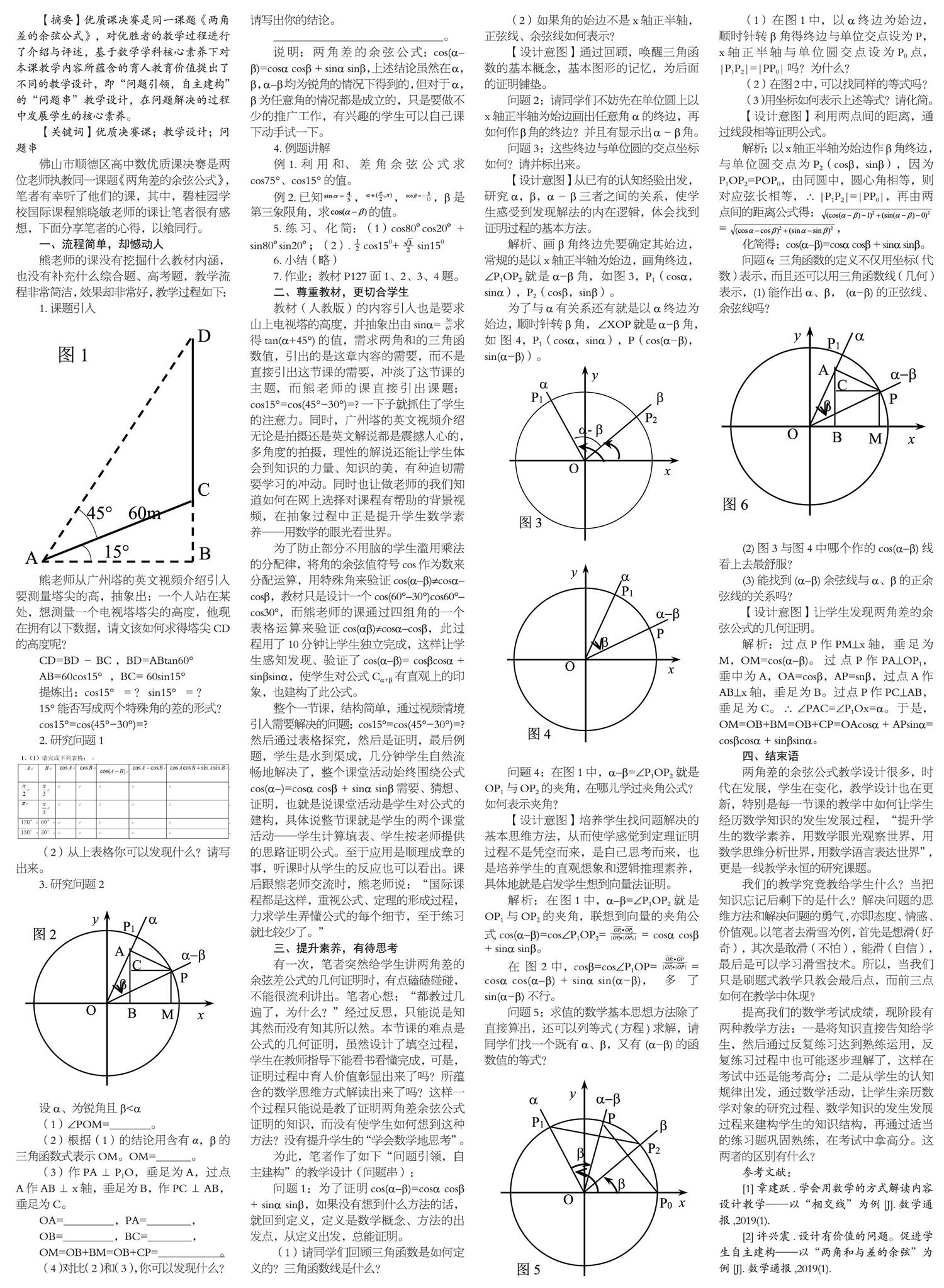
1.課題引入

熊老師從廣州塔的英文視頻介紹引入要測量塔尖的高，抽象出：一個人站在某處，想測量一個電視塔塔尖的高度，他現在擁有以下數據，請文該如何求得塔尖CD的高度呢？

CD=BD-BC ，BD=ABtan60°

AB=60cos15°，BC= 60sin15°

提煉出：cos15°=？sin15°=？

15°能否寫成兩個特殊角的差的形式？

cos15°=cos（45°-30°）=？

2.研究問題1

（2）從上表格你可以發現什么？請寫出來。

3.研究問題2

設α、為銳角且β<α

（1）∠POM=? ? ? ? ? ? ?。

（2）根據（1）的結論用含有α，β的三角函數式表示OM。OM=? ? ? ? ? ?。

（3）作PA⊥P1O，垂足為A，過點A作AB⊥x軸，垂足為B，作PC⊥AB，垂足為C。

OA=? ? ? ? ? ? ? ? ，PA=? ? ? ? ? ? ? ，

OB=? ? ? ? ? ? ? ? ，BC=? ? ? ? ? ? ? ，

OM=OB+BM=OB+CP=? ? ? ? ? ? ? ? ? ? ?。

（4）對比（2）和（3），你可以發現什么？請寫出你的結論。

。

說明：兩角差的余弦公式：cos（α?β）=cosα cosβ + sinα sinβ，上述結論雖然在α，β，α?β均為銳角的情況下得到的，但對于α，β為任意角的情況都是成立的，只是要做不少的推廣工作，有興趣的學生可以自己課下動手試一下。

4.例題講解

例1.利用和、差角余弦公式求cos75°、cos15°的值。

例2.已知，，，β是第三象限角，求的值。

5.練習、化簡：（1）cos80?cos20? + sin80?sin20?;（2）.cos150+sin150

6.小結（略）

7.作業：教材P127面1、2、3、4題。

二、尊重教材，更切合學生

教材（人教版）的內容引入也是要求山上電視塔的高度，并抽象出由sinα=求得tan（α+45°）的值，需求兩角和的三角函數值，引出的是這章內容的需要，而不是直接引出這節課的需要，沖淡了這節課的主題，而熊老師的課直接引出課題：cos15°=cos（45°-30°）=？一下子就抓住了學生的注意力。同時，廣州塔的英文視頻介紹無論是拍攝還是英文解說都是震撼人心的，多角度的拍攝，理性的解說還能讓學生體會到知識的力量、知識的美，有種迫切需要學習的沖動。同時也讓做老師的我們知道如何在網上選擇對課程有幫助的背景視頻，在抽象過程中正是提升學生數學素養——用數學的眼光看世界。

為了防止部分不用腦的學生濫用乘法的分配律，將角的余弦值符號cos作為數來分配運算，用特殊角來驗證cos（α?β）≠cosα?cosβ，教材只是設計一個cos（60°?30°）cos60°?cos30°，而熊老師的課通過四組角的一個表格運算來驗證cos（αβ）≠cosα?cosβ，此過程用了10分鐘讓學生獨立完成，這樣讓學生感知發現、驗證了cos（α?β）= cosβcosα + sinβsinα，使學生對公式Cα+β有直觀上的印象，也建構了此公式。

整個一節課，結構簡單，通過視頻情境引入需要解決的問題：cos15°=cos（45°-30°）=？然后通過表格探究，然后是證明，最后例題，學生是水到渠成，幾分鐘學生自然流暢地解決了，整個課堂活動始終圍繞公式cos（α?）=cosα cosβ + sinα sinβ需要、猜想、證明，也就是說課堂活動是學生對公式的建構，具體說整節課就是學生的兩個課堂活動——學生計算填表、學生按老師提供的思路證明公式。至于應用是順理成章的事，聽課時從學生的反應也可以看出。課后跟熊老師交流時，熊老師說：“國際課程都是這樣，重視公式、定理的形成過程，力求學生弄懂公式的每個細節，至于練習就比較少了。”

三、提升素養，有待思考

有一次，筆者突然給學生講兩角差的余弦差公式的幾何證明時，有點磕磕碰碰，不能很流利講出。筆者心想：“都教過幾遍了，為什么？”經過反思，只能說是知其然而沒有知其所以然。本節課的難點是公式的幾何證明，雖然設計了填空過程，學生在教師指導下能看書看懂完成，可是，證明過程中育人價值彰顯出來了嗎？所蘊含的數學思維方式解讀出來了嗎？這樣一個過程只能說是教了證明兩角差余弦公式證明的知識，而沒有使學生如何想到這種方法？沒有提升學生的“學會數學地思考”。