基于“四度六步”教學(xué)法的教學(xué)設(shè)計與實踐

文尚平 戴啟猛

【摘 要】本文以高中人教 A 版必修 1 函數(shù)復(fù)習(xí)課“比較大小”為例，聚焦高考考查的問題，論述運用“溫故—引新—探究—變式—嘗試—提升”六步教學(xué)法架構(gòu)、設(shè)計一節(jié)數(shù)學(xué)復(fù)習(xí)課的方法及教學(xué)實踐，創(chuàng)設(shè)一節(jié)“有溫度、有梯度、有深度、有寬度”的“四度”精彩課堂，以使課堂“生態(tài)”開放而歡快、課堂生成自然、課堂效果明顯、課堂影響深刻。

【關(guān)鍵詞】“四度六步”教學(xué)法 高一復(fù)習(xí)課 教學(xué)設(shè)計

【中圖分類號】G ?【文獻標(biāo)識碼】A

【文章編號】0450-9889（2020）42-0041-06

在以“送教送培”為主題的賓陽縣全體高中數(shù)學(xué)教師數(shù)學(xué)學(xué)科能力培訓(xùn)活動中，戴啟猛老師做了題為《〈中國高考評價體系〉研讀感悟及備考建議》的專題報告，并基于他原創(chuàng)的“四度六步”教學(xué)法的理論框架對文尚平老師執(zhí)教的人教 A 版高一函數(shù)復(fù)習(xí)課“比較大小”進行了點評，現(xiàn)把整節(jié)課的預(yù)設(shè)與實際過程梳理如下。

一、基本情況

學(xué)生來自賓陽縣某普通高中，學(xué)生的數(shù)學(xué)學(xué)習(xí)興趣弱，基礎(chǔ)、習(xí)慣也都比較差，數(shù)學(xué)的獨立思考能力、合作交流能力基本還沒有形成。因此這節(jié)課的定位是基于學(xué)生層次較低的現(xiàn)狀，面向全縣數(shù)學(xué)教師開展一節(jié)章末復(fù)習(xí)的示范課。

二、教學(xué)內(nèi)容及其分析

（一）內(nèi)容

1.高考考向。在近年高考中，關(guān)于初等函數(shù)的考查經(jīng)常以“比較大小”的方式進行。基于素養(yǎng)立意考查學(xué)生解決這一關(guān)鍵問題的方法和學(xué)科精神，基于能力立意考查學(xué)生“代數(shù)運算、函數(shù)與方程”知識的創(chuàng)新意識和應(yīng)用能力，基于知識立意考查學(xué)生“函數(shù)圖象與性質(zhì)”知識與方法的掌握情況。可見，“比較大小”是中學(xué)數(shù)學(xué)常見的基本問題之一。

2.知識圖譜。這部分的知識圖譜見圖 1。

3.內(nèi)容主線。本節(jié)課主要利用代數(shù)運算與函數(shù)來展開“比較大小”的復(fù)習(xí)，尋找代數(shù)式之間的大小關(guān)系。重點是初等函數(shù)（指數(shù)函數(shù)、對數(shù)函數(shù)、冪函數(shù)）的圖象和性質(zhì)的應(yīng)用，同時突出數(shù)形結(jié)合的思想方法。

（二）教學(xué)內(nèi)容說明

進入高中后，學(xué)生的知識得到不斷豐富和發(fā)展，解決問題的能力也不斷得到提升。“數(shù)值的大小比較”最開始應(yīng)該來自數(shù)軸，因為所有實數(shù)都對應(yīng)著數(shù)軸上的一個點，數(shù)軸的方向便規(guī)定了實數(shù)的大小方向。但對一個代數(shù)來說，我們就難以直接判斷兩個代數(shù)的大小了。這時需要通過代數(shù)運算（減法或除法），甚至更高級的函數(shù)工具來解決。隨著變量數(shù)學(xué)的發(fā)展，用函數(shù)的方法比較代數(shù)的大小時，主要利用函數(shù)的圖象和性質(zhì)，也用到與大小比較有關(guān)的其他知識，特別是利用初等函數(shù)的單調(diào)性、導(dǎo)數(shù)判斷函數(shù)單調(diào)性這一些先進的工具。因此，本堂課通過比較大小，旨在將過去一些重要知識重新整理并形成聯(lián)系，提高學(xué)生對知識的綜合應(yīng)用能力。

三、教學(xué)目標(biāo)及其解析

（一）目標(biāo)

1.學(xué)生通過利用函數(shù)的圖象和性質(zhì)比較兩個數(shù)的大小的經(jīng)歷，掌握比較大小的知識、技能與方法。

2.學(xué)生在通過解決比較大小問題后，進一步體會函數(shù)與方程思想，感悟數(shù)形結(jié)合思想方法的重要性，提高自身的推理論證能力。

（二）解析

1.能利用函數(shù)的圖象和性質(zhì)比較兩個數(shù)的大小，包括將兩個數(shù)的大小問題轉(zhuǎn)化為函數(shù)值的比較問題，然后通過函數(shù)的圖象進行觀察比較，并通過函數(shù)的單調(diào)性做出推理分析。

2.進一步培養(yǎng)數(shù)形結(jié)合的思想方法的運用意識，培養(yǎng)學(xué)生學(xué)會將所求與函數(shù)圖象及其圖象上點的坐標(biāo)聯(lián)系起來分析函數(shù)的單調(diào)性的能力，進一步提高學(xué)生的推理論證能力，通過求解或證明具體問題提高學(xué)生的代數(shù)推理的思維能力。

四、教學(xué)問題診斷分析

在教學(xué)設(shè)計中，問題的設(shè)計、生成與變式是追求有效教學(xué)的重要因素，如何從課本習(xí)題出發(fā)，設(shè)計有梯度、有寬度、有深度的問題，需要老師對教材有深度的理解。

在課堂交流中，學(xué)生不懂的時候，需要老師有“把學(xué)生問懂”的智慧，除了“提好”問題，還要提“好問題”，問題的設(shè)計遵循“四度”教學(xué)理念。

在課堂教學(xué)中，解決問題所用到的知識和方法，需要在課前回顧、整理，并給予及時點撥。鑒于學(xué)生基礎(chǔ)較為薄弱的現(xiàn)，在實際教學(xué)中扶著學(xué)生走可能比領(lǐng)著學(xué)生走更合適。在解決問題過程中所遇到的困難可由老師結(jié)合具體情況進行適當(dāng)?shù)囊龑?dǎo)，因為代數(shù)推理能力的培養(yǎng)需要有一個長期的過程，可遵循“六步”教學(xué)策略。

五、教學(xué)支持條件分析

教學(xué)支持條件主要有兩個方面，一是比較大小的題型較多，所用的解決方法也眾多，有必要借助多媒體，采用思維導(dǎo)圖的方式展開本節(jié)的復(fù)習(xí);二是基于函數(shù)的圖象和性質(zhì)，可利用幾何畫板展示函數(shù)的圖象，用數(shù)形結(jié)合的方式比較大小。

六、基于“四度六步”教學(xué)法的教學(xué)過程設(shè)計

（一）溫故—— 復(fù)習(xí)提問，溫故孕新

【問題 1】數(shù)學(xué)中有哪些常用的“比較大小”的知識和方法？

師：從小學(xué)、初中開始，就接觸到了“比較大小”，進入高中后經(jīng)過必修 1 的學(xué)習(xí)，我們對“比較大小”有了更深的認(rèn)識。我們以往有哪些比較大小的知識和方法呢？哪位同學(xué)愿意同我們分享？

生：我們曾學(xué)習(xí)過“數(shù)”的大小比較、“式”（冪函數(shù)、指數(shù)函數(shù)、對數(shù)函數(shù)代數(shù)式）的大小比較。

師：我們常用的“比較大小”的工具有哪些呢？

生：我們常利用數(shù)軸來解決“數(shù)”的大小比較問題，利用函數(shù)圖象和性質(zhì)來解決“式”的大小比較問題。

師：我們常用哪些方法來“比較大小”？

生：在方法上，我們常用做差或者做商比較法、函數(shù)的單調(diào)性法、圖象法。

〖設(shè)計意圖〗該問題的設(shè)計試圖遵循“一明一暗”兩條線原則。明線是比較大小的知識結(jié)構(gòu)：數(shù)的大小比較—— 代數(shù)式的大小比較—— 變量數(shù)學(xué)中的大小比較。暗線是比較大小的思想方法：從數(shù)軸上兩個數(shù)的大小比較，到通過做差（或做商）比較大小，再到利用函數(shù)的圖象和性質(zhì)比較大小，最后到利用導(dǎo)數(shù)比較大小。

〖評析〗問題的設(shè)計也是由具體知識到解決問題工具再到解決問題思想方法的回顧，梯度呈現(xiàn)，逐步形成體系。“一明一暗”將中學(xué)數(shù)學(xué)的很多重要內(nèi)容串聯(lián)起來，形成了一條具有豐富思想方法的知識線索。教學(xué)的目標(biāo)非常巧妙地“孕”藏其中，一句“哪位同學(xué)愿意同我們分享？”更是充滿老師真切的期待，讓學(xué)生聽起來倍受激勵，倍感溫暖。

師：大家回答得都很好。同學(xué)們不僅提到了“比較大小”相關(guān)的知識，也提到了“比較大小”的具體方法、工具。我們知道，數(shù)學(xué)中的“大小比較”，經(jīng)歷了“數(shù)—— 代數(shù)式—— 變量數(shù)學(xué)”三個階段。那么，高考又是怎樣考查比較大小的呢？請看問題 2。

【問題 2】請同學(xué)們根據(jù)下面高考試題的結(jié)構(gòu)特點，思考這道試題考查的是什么問題，以及考查了哪些已經(jīng)學(xué)過的內(nèi)容？

（2017 年課標(biāo) 1，理 11）若 x，y∈R+，且 2x=3y=5z，則（ ?）。

A.2x<3y<5z B.5z<2x<3y

C.3y<5z<2x D.3y<2x<5z

生：本題考查的是“式”的大小比較問題。

生：本題考查了指數(shù)與對數(shù)的相互轉(zhuǎn)化，指數(shù)、對數(shù)運算的知識，以及指數(shù)與對數(shù)函數(shù)的圖象和性質(zhì)等相關(guān)知識。

〖設(shè)計意圖〗復(fù)習(xí)課需要有高考的站位，“以考為向，以學(xué)定教”。先拋出這一典型且有挑戰(zhàn)性的高考真題但并不著急解決（具體求解留在“師生互動，變式深化”環(huán)節(jié)），而是引導(dǎo)學(xué)生先挖掘此高考真題中考查的小問題—— 具體問題的知識、結(jié)構(gòu)特點，從而展開指、對、冪函數(shù)圖象和性質(zhì)的復(fù)習(xí)，理清高考中“比較大小”知識考查的主線，明確高考考查的重點、難點、熱點，準(zhǔn)確把握“比較大小”的考查要求，為學(xué)生科學(xué)備考提供依據(jù)。

師生活動：基于這一道高考題考查的關(guān)鍵問題，回顧前面已經(jīng)學(xué)習(xí)過的指數(shù)函數(shù)、對數(shù)函數(shù)、冪函數(shù)的圖象和性質(zhì)（如表 1）。

〖設(shè)計意圖〗復(fù)習(xí)鞏固這三個初等函數(shù)的圖象和性質(zhì)，為本節(jié)課“比較大小”的學(xué)習(xí)搭好梯子、架子。在內(nèi)容的呈現(xiàn)上，表格更直觀形象。

〖評析〗瑞士現(xiàn)代兒童心理學(xué)家讓·皮亞杰認(rèn)為：“學(xué)習(xí)并不是個體獲得越來越多外部信息的過程，而是學(xué)到越來越多有關(guān)他們認(rèn)識事物的程序，即建構(gòu)了新的認(rèn)識圖式。”（圖式是皮亞杰理念體系中的一個核心概念，是指個體對世界的知覺、理解和思考的方式。我們可以把圖式看作是心理活動的框架或組織結(jié)構(gòu)。在皮亞杰看來，圖式可以說是認(rèn)知結(jié)構(gòu)的起點和核心，或者說是人類認(rèn)識事物的基礎(chǔ)。因此，圖式的形成和變化是認(rèn)知發(fā)展的實質(zhì)）為此，筆者主張的“溫故”策略，教師的設(shè)計應(yīng)把握三個技術(shù)要領(lǐng)：一是“溫故”應(yīng)指向前一課學(xué)習(xí)的主要內(nèi)容，二是“溫故”應(yīng)指向與本節(jié)新課關(guān)聯(lián)的知識，三是“溫故”應(yīng)設(shè)計為孕育新知鋪墊的問題。本課設(shè)計的“復(fù)習(xí)提問，溫故孕新”環(huán)節(jié)，從數(shù)值的大小比較到變量數(shù)學(xué)的大小比較，不僅體現(xiàn)數(shù)學(xué)知識獨特的邏輯和系統(tǒng)，而且是在復(fù)習(xí)舊知識的過程中蘊含新的教學(xué)內(nèi)容，為新知識的教學(xué)鋪平道路，充分詮釋復(fù)習(xí)提問的意義和數(shù)學(xué)教學(xué)的藝術(shù)。

（二）引新—— 創(chuàng)設(shè)情境，引入課題

師：有了前面的基礎(chǔ)，下面我們圍繞“式”的大小比較展開本節(jié)課的學(xué)習(xí)。同學(xué)們能解決下面的問題嗎？

【例 1】（課本 59 頁，第 7 題）比較下列各組數(shù)的大小。

（1）30.8，30.7? ? ? ? ? ? ? ? （2）1.012.7，1.013.5

（3）0.75-0.1，0.750.1? ? ? （4）0.993.3，0.994.5

生：（1）（2）同底數(shù)，則利用指數(shù)函數(shù) y=3x，y=1.01x 的單調(diào)遞增性質(zhì);（3）（4）同底數(shù)，則利用指數(shù)函數(shù) y=0.75x，y=0.99x 的單調(diào)遞減性質(zhì)。

師：同底數(shù)、不同指數(shù)的指數(shù)式，我們常利用指數(shù)函數(shù)的單調(diào)性比較大小。可是，如果是指數(shù)同、底數(shù)不同，甚至底數(shù)、指數(shù)都不同的情況下，那么又怎么比較大小？

〖變式1〗比較下列各組數(shù)的大小。

（1） （2）

（3） ? ? ? （4）

生：（1）同指數(shù) 0.5，利用冪函數(shù) y=x0.5 的單調(diào)遞增性質(zhì);（2）底數(shù)不同，化為同底 3，再利用函數(shù) y=3x 的單調(diào)遞增性質(zhì);（3）指數(shù)不同，化為同指數(shù) 5，再利用函數(shù) y=x5 的單調(diào)遞增性質(zhì);（4）如既不能化為同底，又不能化為同指，則利用中間量 1，與 1 比較。

〖設(shè)計意圖〗通過題組訓(xùn)練，聚焦冪值大小比較最常見的三種情形，指導(dǎo)學(xué)生掌握這三種題型的基本解題思路，掌握解題過程中相關(guān)的思想方法。

師生活動：歸納、整理比較指數(shù)式大小的一般思路和方法，如圖 2。

圖 2

〖評析〗此環(huán)節(jié)設(shè)計是基于學(xué)生已有的知識和經(jīng)驗，從課本習(xí)題出發(fā)，對課本習(xí)題進行變式，引導(dǎo)學(xué)生復(fù)習(xí)、思考底數(shù)、冪指數(shù)發(fā)生變化的情況下指數(shù)式大小比較的差異。遷移運用知識，強化從特殊到一般的解決問題的數(shù)學(xué)思維方法。課堂教學(xué)不僅要指向核心的學(xué)習(xí)內(nèi)容，而且要體現(xiàn)數(shù)學(xué)課堂應(yīng)有的梯度，保證課堂教學(xué)得到“托底”。

（三）探究—— 合作探究，活動領(lǐng)悟

師：類比指數(shù)式的大小比較的復(fù)習(xí)方式，請同學(xué)們談?wù)剬?shù)式大小比較的復(fù)習(xí)方法。

生：在順序上，我們先復(fù)習(xí)底數(shù)同、真數(shù)同的對數(shù)式的大小比較，再復(fù)習(xí)底數(shù)、真數(shù)都不同的對數(shù)式大小比較。

生：在策略上，應(yīng)該利用對數(shù)函數(shù)的圖象和性質(zhì)。

師：根據(jù)同學(xué)們的想法，下面我們從一道課本習(xí)題出發(fā)，復(fù)習(xí)對數(shù)式大小比較的一般解法。

【例 2】（課本第 73 頁，第 3 題）比較下列各題中兩個值的大小。

（1）lg 6，lg 8 ? ? （2）log0.5 6，log0.5 4

（3） ? ? （4）log1.5 1.6，log1.5 1.4

生：都是同底數(shù)，分別利用對數(shù)函數(shù) y=lg x，log0.5 x，，log1.5 x 的單調(diào)性。

師：如果底數(shù)不同，甚至底數(shù)、真數(shù)都不同，那么又怎么比較大小？請同學(xué)們根據(jù)下面的變式題前后四人小組討論，提出解決問題的思路和方法。

〖變式 2〗比較下列各組數(shù)的大小。

（1）log0.3 7，log9 7 （2）log6 7，log7 6 （3）log3 π，log2 0.8

師：底數(shù)不同的情況下，我們有辦法化為同底數(shù)嗎？

生：換底公式 。

師：這 3 個問題的解題過程是怎樣的？

生：（1）真數(shù)同，利用換底公式，或者底大圖低（x>1）的規(guī)律;（2）（3）底數(shù)、真數(shù)都不同，利用中間量 1，0。

〖設(shè)計意圖〗通過題組訓(xùn)練，聚焦對數(shù)值大小比較最常見的三種情形，并指導(dǎo)學(xué)生掌握這三種題型的基本解題思路，掌握解題過程中相關(guān)的思想方法。

師生活動：師生合作，歸納、整理比較指數(shù)式大小的一般思路和方法，如圖 3。

〖評析〗什么是探究學(xué)習(xí)？探究學(xué)習(xí)是指學(xué)生在教師指導(dǎo)下，以類似科學(xué)研究的方式去主動獲取知識、運用知識、解決問題、形成觀點的一種學(xué)習(xí)。這種學(xué)習(xí)不沉湎于純粹的數(shù)學(xué)知識，也不直接給出現(xiàn)成的結(jié)論，而是讓學(xué)生在理論學(xué)習(xí)、史料閱讀、問題討論、動手操作、課題研究中獲得學(xué)習(xí)能力、掌握學(xué)習(xí)方法，從而學(xué)會學(xué)習(xí)。顯然，探究式學(xué)習(xí)改變了以往學(xué)生被動接受學(xué)習(xí)的現(xiàn)狀。教師應(yīng)創(chuàng)造條件讓學(xué)生能積極主動地去探索、嘗試，更好地發(fā)揮個體創(chuàng)造潛能，真正成為學(xué)習(xí)的主人。“探究”策略應(yīng)把握二個技術(shù)要領(lǐng)：一是“探究”的關(guān)鍵是設(shè)計好的數(shù)學(xué)問題;二是“探究”的實效是學(xué)生參與的廣度和深度。本環(huán)節(jié)類比指數(shù)式大小比較的學(xué)習(xí)，引導(dǎo)學(xué)生思考底數(shù)、真數(shù)發(fā)生變化的情況下的對數(shù)式大小比較的差異。通過“合作探究，活動領(lǐng)悟”實現(xiàn)知識的遷移應(yīng)用，強化從特殊到一般獲得問題解決的數(shù)學(xué)思維方法。由師生合作系統(tǒng)歸納對數(shù)式的大小比較方法，讓學(xué)生在進一步領(lǐng)悟數(shù)學(xué)學(xué)習(xí)的本質(zhì)，體現(xiàn)數(shù)學(xué)課堂應(yīng)有的思維深度。

（四）變式—— 師生互動，變式深化

師：通過上述兩個問題，我們復(fù)習(xí)歸納了常見的有關(guān)冪值、對數(shù)值大小比較的題型及方法，歸根結(jié)底，最終都是回到初等函數(shù)的圖象和性質(zhì)的應(yīng)用上。然而，高考中有關(guān)大小的比較問題的形式遠不止這些，請同學(xué)看下面的問題。

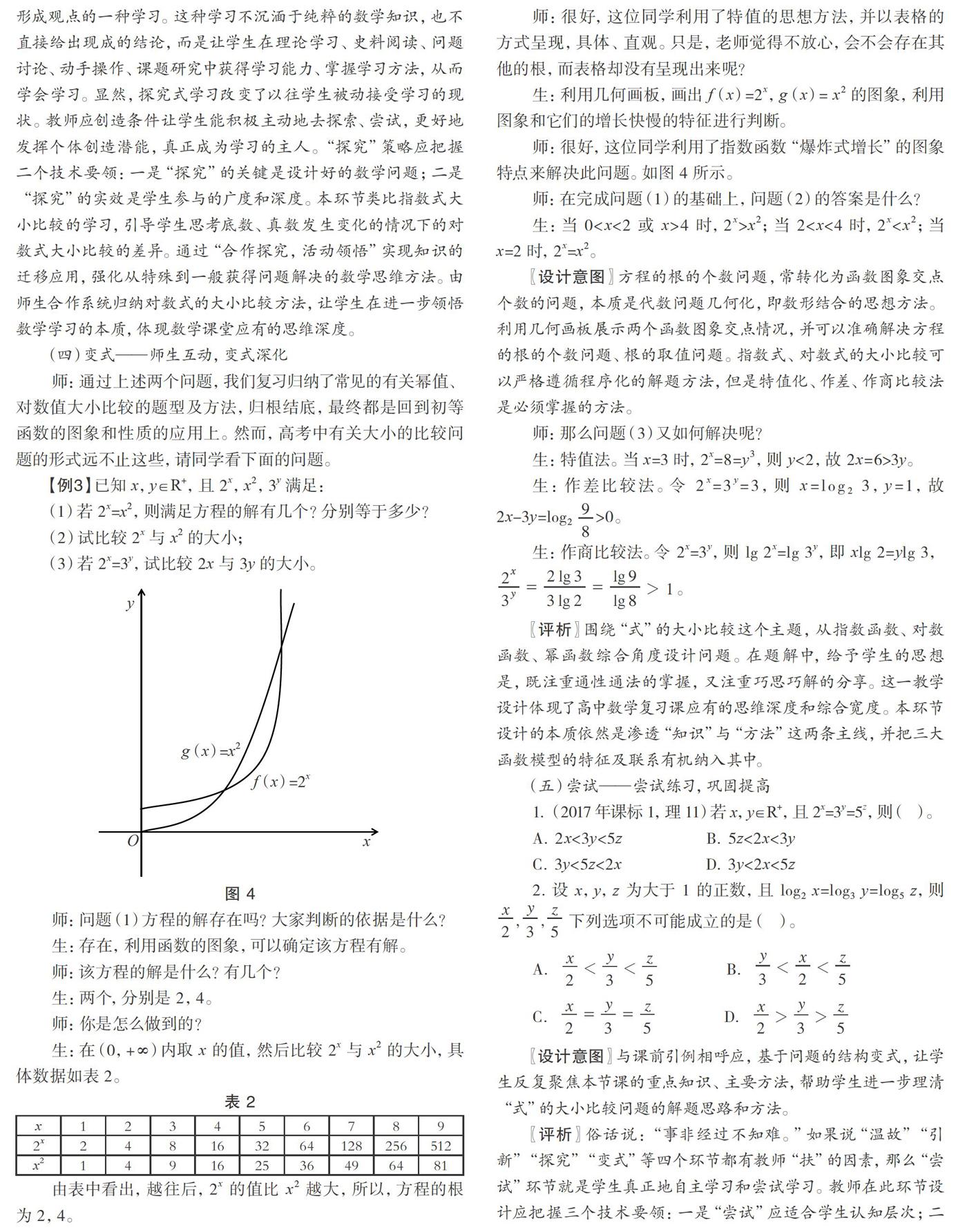
【例3】已知 x，y∈R+，且 2x，x2，3y 滿足：

（1）若 2x=x2，則滿足方程的解有幾個？分別等于多少？

（2）試比較 2x 與 x2 的大小;

（3）若 2x=3y，試比較 2x 與 3y 的大小。

師：問題（1）方程的解存在嗎？大家判斷的依據(jù)是什么？

生：存在，利用函數(shù)的圖象，可以確定該方程有解。

師：該方程的解是什么？有幾個？

生：兩個，分別是 2，4。

師：你是怎么做到的？

生：在（0，+∞）內(nèi)取 x 的值，然后比較 2x 與 x2 的大小，具體數(shù)據(jù)如表 2。

由表中看出，越往后，2x 的值比 x2 越大，所以，方程的根為 2，4。

師：很好，這位同學(xué)利用了特值的思想方法，并以表格的方式呈現(xiàn)，具體、直觀。只是，老師覺得不放心，會不會存在其他的根，而表格卻沒有呈現(xiàn)出來呢？

生：利用幾何畫板，畫出 f（x）=2x，g（x）= x2 的圖象，利用圖象和它們的增長快慢的特征進行判斷。

師：很好，這位同學(xué)利用了指數(shù)函數(shù)“爆炸式增長”的圖象特點來解決此問題。如圖 4 所示。

師：在完成問題（1）的基礎(chǔ)上，問題（2）的答案是什么？

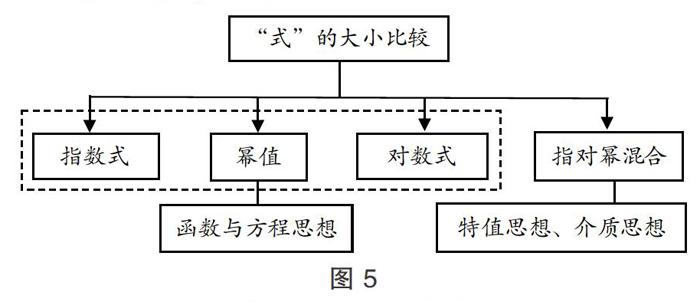
生：當(dāng) 04 時，2x>x2;當(dāng) 2

〖設(shè)計意圖〗方程的根的個數(shù)問題，常轉(zhuǎn)化為函數(shù)圖象交點個數(shù)的問題，本質(zhì)是代數(shù)問題幾何化，即數(shù)形結(jié)合的思想方法。利用幾何畫板展示兩個函數(shù)圖象交點情況，并可以準(zhǔn)確解決方程的根的個數(shù)問題、根的取值問題。指數(shù)式、對數(shù)式的大小比較可以嚴(yán)格遵循程序化的解題方法，但是特值化、作差、作商比較法是必須掌握的方法。

師：那么問題（3）又如何解決呢？

生：特值法。當(dāng) x=3 時，2x=8=y3，則 y<2，故 2x=6>3y。

生：作差比較法。令 2x=3y=3，則 x=log2 3，y=1，故 2x-3y=log2 >0。

生：作商比較法。令 2x=3y，則 lg 2x=lg 3y，即 xlg 2=ylg 3，。

〖評析〗圍繞“式”的大小比較這個主題，從指數(shù)函數(shù)、對數(shù)函數(shù)、冪函數(shù)綜合角度設(shè)計問題。在題解中，給予學(xué)生的思想是，既注重通性通法的掌握，又注重巧思巧解的分享。這一教學(xué)設(shè)計體現(xiàn)了高中數(shù)學(xué)復(fù)習(xí)課應(yīng)有的思維深度和綜合寬度。本環(huán)節(jié)設(shè)計的本質(zhì)依然是滲透“知識”與“方法”這兩條主線，并把三大函數(shù)模型的特征及聯(lián)系有機納入其中。

（五）嘗試—— 嘗試練習(xí)，鞏固提高

1.（2017 年課標(biāo) 1，理 11）若 x，y∈R+，且 2x=3y=5z，則（ ?）。

A.2x<3y<5z B.5z<2x<3y

C.3y<5z<2x D.3y<2x<5z

2.設(shè) x，y，z 為大于 1 的正數(shù)，且 log2 x=log3 y=log5 z，則 ?下列選項不可能成立的是（ ?）。

A.B.

C.D.

〖設(shè)計意圖〗與課前引例相呼應(yīng)，基于問題的結(jié)構(gòu)變式，讓學(xué)生反復(fù)聚焦本節(jié)課的重點知識、主要方法，幫助學(xué)生進一步理清“式”的大小比較問題的解題思路和方法。

〖評析〗俗話說：“事非經(jīng)過不知難。”如果說“溫故”“引新”“探究”“變式”等四個環(huán)節(jié)都有教師“扶”的因素，那么“嘗試”環(huán)節(jié)就是學(xué)生真正地自主學(xué)習(xí)和嘗試學(xué)習(xí)。教師在此環(huán)節(jié)設(shè)計應(yīng)把握三個技術(shù)要領(lǐng)：一是“嘗試”應(yīng)適合學(xué)生認(rèn)知層次;二是“嘗試”應(yīng)指向新知鞏固提高;三是“嘗試”應(yīng)及時回授練習(xí)效果。教師在講評中再次強調(diào)：“類似本題所討論的比較大小的問題，既可以轉(zhuǎn)化為兩個函數(shù)來分析，又可以做差后轉(zhuǎn)化為利用一個函數(shù)的圖象和性質(zhì)進行分析。當(dāng)然，通過幾何畫板作圖求值，能為我們提出問題和分析問題提供更加直觀而便捷的幫助。”充分彰顯“嘗試練習(xí)，鞏固提高”的應(yīng)有之意。

（六）提升—— 適時小結(jié)，興趣延伸

師：同學(xué)們能否畫一個結(jié)構(gòu)圖表示這節(jié)課所學(xué)的內(nèi)容？

學(xué)生畫出的知識結(jié)構(gòu)圖如圖 5 所示。

〖評析〗在課堂教學(xué)中，筆者主張的“提升”策略應(yīng)把握三個技術(shù)要領(lǐng)：一是幫助學(xué)生解開思維疙瘩，恰時點撥;二是指向主要知識方法思路，恰點歸納;三是重在激發(fā)學(xué)生學(xué)習(xí)興趣，恰到好處。其實，在本節(jié)課例中，老師在此環(huán)節(jié)只是對原有的教學(xué)板書進行適當(dāng)?shù)难a充和完善，對關(guān)鍵的思想方法進行必要的重復(fù)和強調(diào)。因為他在前述的教學(xué)過程中已經(jīng)做到了恰時點撥，恰點歸納，恰當(dāng)激勵。

七、課后作業(yè)（略）

八、板書設(shè)計（略）

九、課后總評

（一）“四度六步”教學(xué)法的理論框架

“四度六步” 教學(xué)法，是戴啟猛老師歷時 20 年教研實踐后提出的數(shù)學(xué)教育教學(xué)主張和策略，是以追求“四度”（有溫度、有梯度、有深度和有寬度）精彩課堂為目的，遵照“溫故（復(fù)習(xí)提問，溫故孕新）—— 引新（創(chuàng)設(shè)情境，引入課題）—— 探究（合作探究，活動領(lǐng)悟）—— 變式（師生互動，變式深化）——嘗試（嘗試練習(xí)，鞏固提高）—— 提升（適時小結(jié)，興趣延伸）”六個環(huán)節(jié)精準(zhǔn)設(shè)計和組織的初中數(shù)學(xué)教學(xué)方法。其中，“四度”課堂是教學(xué)主張、教學(xué)理念，“六步”環(huán)節(jié)是實踐架構(gòu)，也是教學(xué)策略。“四度六步”教學(xué)法的目標(biāo)是創(chuàng)造更加精彩的課堂。操作模型如圖 6 所示。

（二）用“四度六步”教學(xué)法指導(dǎo)高中單元（章末）復(fù)習(xí)課的步驟

基于“四度六步”教學(xué)法的數(shù)學(xué)單元（章末）復(fù)習(xí)課的教學(xué)任務(wù)是：“構(gòu)建網(wǎng)絡(luò)，提煉模型，形成思想，學(xué)會思辨。”其結(jié)構(gòu)是：“溫故引新，構(gòu)建網(wǎng)絡(luò);探究合作，提煉模型;問題變式，形成思想;嘗試提升，學(xué)會思辨。”

1.溫故—— 復(fù)習(xí)提問，溫故孕新。以重溫知識、構(gòu)建知識網(wǎng)絡(luò)為目的，其作用是將零碎的知識點系統(tǒng)化，形成知識體系。“溫故”既指向前單元典型問題學(xué)習(xí)的主要內(nèi)容，又指向與本節(jié)復(fù)習(xí)課關(guān)聯(lián)的知識，同時要注意為孕育新知識、方法做鋪墊的設(shè)計。

2.引新—— 創(chuàng)設(shè)情境，引入課題。提煉出單元典型問題的解題模型，進而對模型進行固化，其作用是在建模和解模的過程中滲透基本方法、基本技能和基本活動經(jīng)驗。“引新”應(yīng)基于學(xué)生已有的知識和經(jīng)驗，應(yīng)指向教學(xué)目標(biāo)和核心內(nèi)容，但要遵循思考性、探索性和開放性的基本原則。

3.探究—— 合作探究，活動領(lǐng)悟。通過合作學(xué)習(xí)，將典型問題與其他知識板塊進行交匯、拓展、引申，讓學(xué)生在解決問題的過程中形成并發(fā)展數(shù)學(xué)思維，其作用是讓學(xué)生體驗章末復(fù)習(xí)的基本流程。“探究”的關(guān)鍵是設(shè)計好的數(shù)學(xué)問題，指向?qū)W生課堂參與的廣度和深度。

4.變式—— 師生互動，變式深化。通過對問題進行變式教學(xué)，開展一題多解、多題一解的教學(xué)活動，固化問題求解模型，從而內(nèi)化為思想，其作用是解決學(xué)生聽得懂課而不會解題的困惑。“變式”應(yīng)遵循教學(xué)的實際，也應(yīng)把握設(shè)計的梯度，還應(yīng)指向知識的本質(zhì)。

5.嘗試—— 嘗試練習(xí)，鞏固提高。指通過指導(dǎo)學(xué)生用數(shù)學(xué)的眼光觀察現(xiàn)實世界，用數(shù)學(xué)模型解決現(xiàn)實問題，用數(shù)學(xué)語言表達現(xiàn)實世界，其作用是鞏固所學(xué)知識，發(fā)展數(shù)學(xué)思維。“嘗試”應(yīng)適合學(xué)生認(rèn)知規(guī)律，也應(yīng)指向新知鞏固和提高，還應(yīng)及時回授以取得練習(xí)效果。

6.提升—— 適時小結(jié)，興趣延伸。通過思辨，培養(yǎng)學(xué)生的應(yīng)用意識和創(chuàng)新意識。其作用是引導(dǎo)學(xué)生思考問題和探討解法的異同，從而適時感悟?qū)W習(xí)規(guī)律，及時提煉方法。“提升”應(yīng)幫助學(xué)生解開思維疙瘩，適時點撥，也應(yīng)指向主要知識、方法、思路。恰當(dāng)歸納，還應(yīng)以激發(fā)學(xué)生學(xué)習(xí)興趣，恰到好處為基本原則。

“四度六步”教學(xué)法以精彩的數(shù)學(xué)課堂為追求目標(biāo)，而一節(jié)精彩的數(shù)學(xué)課，關(guān)鍵在于課堂的生態(tài)、師生的狀態(tài)。在精彩的數(shù)學(xué)課堂中，學(xué)生應(yīng)該是開放的、歡快的，應(yīng)該能看到孩子們自信的眼神，聽到孩子們生長的聲音，使師生的心得到舒展，情感得到升華。這個課例不僅遵循“四度六步”教學(xué)法所倡導(dǎo)的理念和程式，而且較好地詮釋了“四度六步”教學(xué)法，讓我們感受到一節(jié)精彩的高中數(shù)學(xué)復(fù)習(xí)課的驚人效果和獨特魅力。

【參考文獻】

[1]戴啟猛.創(chuàng)造更加精彩的課堂——初中數(shù)學(xué)“四度六步”教學(xué)法的20年實踐與探索[J].廣西教育，2020（2）.

[2]段小龍，葉 強，羅文平.基于“問題驅(qū)動”下的數(shù)學(xué)單元（章末）復(fù)習(xí)課的教學(xué)設(shè)計[J].數(shù)學(xué)通訊（下半月），2018（9）.

[3]戴啟猛.基于初中數(shù)學(xué)“四度六步”教學(xué)法的理論基礎(chǔ)與實踐架構(gòu)[J].中小學(xué)課堂教學(xué)研究，2020（3）.

【基金項目】本文系2021年廣西“十四五”教育科學(xué)規(guī)劃B類重點課題“基于核心素養(yǎng)下高中數(shù)學(xué)‘學(xué)、教、評一致性教學(xué)設(shè)計的理論與實踐研究”（2021B200）的階段成果。

【作者簡介】文尚平，碩士研究生，高級教師，南寧市第二中學(xué)教師，南寧市學(xué)科帶頭人，廣西基礎(chǔ)教育名師青藍工程培養(yǎng)對象，廣西教育科學(xué)研究院、南寧市教科所數(shù)學(xué)學(xué)科中心組成員，競賽教練，第5屆全國數(shù)學(xué)優(yōu)質(zhì)課比賽一等獎獲得者;戴啟猛，正高級教師，南寧市教育科學(xué)研究所所長，廣西“21世紀(jì)園丁工程”首批百名自治區(qū)級（A類）培養(yǎng)對象、教育部全國（萬名）中小學(xué)骨干教師培養(yǎng)對象、廣西“基礎(chǔ)教育百名名校長工程”培養(yǎng)對象，教育部“校長教育家工程”培養(yǎng)對象。

（責(zé)編 盧建龍）