初中數學“圖形與幾何”入門教學分析

楊美蓮

摘 要：相比于小學的數學知識內容而言，初中所涉及的數學知識十分廣泛，而且難度性也比較大。在初中數學教材中“圖形與幾何”是一個重要的教學內容，對此，不僅需要學生們具備一定的數學邏輯思維能力，而且還需要學生們具有探索精神、靈活運用能力和觀察能力。

關鍵詞：初中數學;圖形與幾何;入門教學;教學分析

學生難學，教師難教，這句話能夠很好的反應出“圖形與幾何”所處于兩難的位置之間。面對在教學中這樣一個難題，就需要教師在教學方法和策略上不斷尋求創新，以學生的數學學習綜合能力和發展為重點，幫助學生們能夠靈活的運用數學知識解決“圖形與幾何”相關的問題。

1.初中數學“圖形與幾何”教學策略的內涵

雖然國家對教育不斷的進行了改革和創新，以學生們的綜合實踐能力為教學的重點，但是，由于受到傳統教學觀念的影響，很難積極的落實這項改革，轉變傳統的死記硬背和題海戰術。教師在進行“圖形與幾何”的課堂教學時，首先需要迎合實際尋求創新，通過不斷豐富自身的課堂教學策略，來引導和幫助學生找到學習解決“圖形與幾何”相關的數學問題，教師要以相關的數學知識內容為教學的基礎，以每位學生的學習能力和理解能力為向導，以教學實情為前提，并積極的落實相關的課堂教學策略，使“圖形與幾何”教學策略更加完善，凸顯出它的作用和效果，從而提高初中數學課堂教學質量和水平。

2.初中數學“圖形與幾何”入門教學策略分析

2.1激發興趣，消除心理障礙

興趣是最好的老師，它能夠幫助學生消除對“圖形與幾何”相關數學問題上心理的障礙，讓其集中注意力的去學習、發現和探索，并產生一種放松、愉快的學習心理，最終，有效的提高學生們學習數學知識的質量和效率，所以，教師做好興趣教學是十分重要的。教師可以從以下幾個方面來激發學生學習“圖形與幾何”數學知識的積極性，結合教材內容和教學內容從幾何的實用性、趣味性以及幾何推理的嚴密性和邏輯性等這幾個方面來激發學生們學習的興趣、積極性。

2.2培養學生們的推理能力

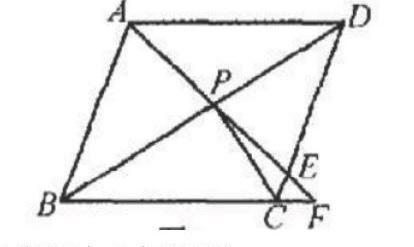
一定的推理能力是學生們學習幾何數學知識內容的基礎，同時也是決定入門與否的關鍵性因素，由此可以看出教師培養學生們推理能力的重要性。在眾多考察學生們是否有一定的幾何推理能力的方法中，讓學生們利用書寫解題的方法展現給教師是最直觀、最準確的方法之一，教師能夠在批改學生們解題過程的同時，發現并找到每位同學在幾何推理中所出現的一些現存問題，此時，教師就可以針對這些問題展開針對性的教學和指導。推理過程主要圍繞四大階段展開推理，第一階段，學生可以根據圖形回答出相應的答案;第二階段，學生用自己的語言來敘述的方式證明已掌握、學習的定理，用相應的數學形式、符號把其表示出來;第三階段，用探索分析的方法推證判定結論，縷清解題的主要思路，規范寫出推理的形式;第四階段，結合自身的邏輯知識，寫出相應的證明過程。例如：教師可以為學生們設計一個例題，讓學生們自己推理出基本的數學推理公式，并寫出證明的各個過程和步驟，讓學生們掌握不同推理模式的形式，教師就可以通過這種方式幫助學生們培養數學推理能力的養成。例如：下圖的菱形ABCD中，BD上有一點p，將AP延長，和CD相交于E，和BS延長線相交于F.證明：PC2=PE·PF.

求證 PC2=PE·PF，我們可以求證條件轉變一下形式，就得PC/PE=PF/PC;此時我們只需要證明△FPC與CPE相似.∠CPF是是兩者三角形的公共角.對此，只需要證明：∠F=∠PAD即可.根據已知條件中和菱形的性質我們可以得出：∠BDA=∠CDB，AD=CD，可得，△PAD全等于△PCD.所以∠PAD=∠PCD.又因為AD//BF，可知∠PAD=∠F，所以∠PCD=∠F.因此，PC2=PE·PF成立。

2.3利用輔助線解決幾何問題

輔助線可以幫助學生們把常見的幾何問題劃分成不同的小問題，把這些小問題逐

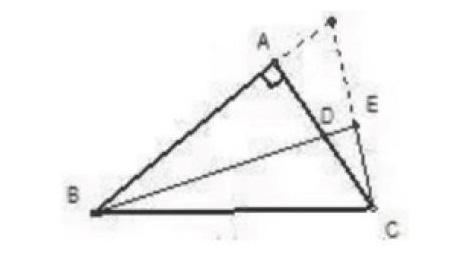
個擊破就可以得到解題的答案。在一部分的數學幾何問題中，有時候我們很難根據題意找到并寫出解題的答案，需要我們善于捕捉圖形和幾何中隱藏起來的一些小問題，抓住每道題目中不同的要點，試著畫一些輔助線，試著自己不斷的摸索和探索，數學問題就可以迎刃而解了。例如：在下圖中，AB=AC，BA⊥AC，BD是∠ABC的平分線，CE⊥BE。求證：BD=2CE。此時，就可以運用做輔助線的方法去解決這道數學題，可以延長此垂線與另外一邊相交，得到等腰三角形，隨后證明全等就可以。它利于學生們的自主探索精神的培養和養成，只要在我們的腦中有一些解題的想法，就需要我們去嘗試和驗證，它是幫助我們解題的基礎。

結束語：

綜上所述，“圖形與幾何”相關的數學知識內容不僅是教學的重點，同時也是數學課堂教學中一大難點，教師要對教學策略尋求創新，需要結合自身的經驗展開教學，從多方面、多途徑來幫助學生更好的理解、吸收和消化“圖形與幾何”的知識點，從根本出發來激發學生們學習數學的自主性和積極性，從而有效的提高數學課堂教學質量和水平。

參考文獻：

[1]范成.初 中數學幾何推理與圖形證明策略例談[J]. 數理化解題研 究（初 中版 ），2014（10）

[2]沈定祥.淺談“基本圖形”在初中數學幾何教學證明中 的作用[J].新課程學習（下），2014（O6）

[3]呂明.初中數學“空間與圖形”的入 門教學[J].課程 教材教學研究（中教研究），2013（Z5）