小學數學結構化教學思維的建構策略

周鳳花

【摘要】文章在結構化思維教學方式的主導與建模的基礎上，從關注單元知識結構化設計，關注階段性知識結構化設計，關注教材重組結構化設計，關注階段性復習中教學過程的設計四個方面入手，對實現結構化教學思維的構建提出了具有建設性的建議。

【關鍵詞】小學數學;結構化教學思維;建構策略

【基金項目】本文系2018年福建省中青年教師教育科研項目（基礎教育研究專項）課題“構建思理相生小學數學課堂的實踐研究”中期研究成果，課題立項批準號：JZ180228。

通常而言，結構化教學思維的構建在培養學生思維品質方面發揮了重要作用：一方面，有利于激發學生學習的積極性和主動性，培養學生自主學習能力和自主探究能力;另一方面，有利于培養獨立思考的意識，為促進學生的智力發育打下堅實的基礎。因此，如何科學構建結構化教學思維是教師在小學數學教學過程中必須思考和解決的問題。

一、關注單元知識結構化設計

首先，教師要樹立系統、整體的教學觀念，在新課開始之前，要做好對單元知識的結構化設計，通過采用構建橫向架構的方式，在教學過程中滲透和融入相關知識點，從而提高學生的學習效率和效果。

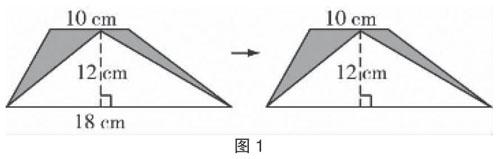
例如，復習“多邊形面積”相關知識時，教師為學生布置一道練習題：如圖1左所示，求解陰影部分的面積。

全班幾乎所有學生都采用“梯形面積與三角形面積之差”的方式進行求解。教師在這道練習題的基礎上，去掉了一個已知條件，即“梯形的底邊長”，要求學生求出陰影部分的面積。此時，學生有點無計可施，不知道如何解答。如果教師利用假設法講解這道練習題，顯然不符合教學的目標和要求[1]。因此，教師利用三角形面積相關推導思想，以常規解題思路為起點，設計出以下解題步驟，幫助學生進行引導和探究，將會取得意想不到的教學效果。

第一，分別畫出長方形、平行四邊形，然后分別沿著兩個圖形的對角線將其分成大小相同的兩個三角形，并探究出三角形與長方形、平行四邊形兩個之間的關系，即“等底等高”的關系。由此得出一個結論：三角形的面積是等底等高長方形或者平行四邊形面積的一半。

第二，如圖2所示，沿著長方形或者平行四邊形的底邊，對三角形的某一個頂點進行移動，可以得到不同形狀的三角形，試問所有不同形狀的三角形面積是否均為長方形或者平行四邊形面積的一半？如果是，請說出理由。

第三，進入拓展環節。在兩個面積和形狀都一樣的長方形或者平行四邊形中，找出其中面積最大的三角形。

第四，進入推理環節[2]。將長方形分割成兩個不同形狀的三角形，分析兩個三角形的面積之和與長方形面積之間的關系，如果分割成三個或四個三角形又有什么關系？

第五，進入延伸環節。有了上面的知識儲備后，同學們對如何將兩個三角形面積轉化為一個三角形面積有了一個新的認識和體會。此時，為學生設計以下練習題：“長方形的長和寬分別為25cm和10cm，試計算出陰影面積。”學生在解答這類題目時就會輕而易舉、迎刃而解。然后回到最開始的練習題，利用以上規律，將陰影部分轉化為一個三角形進行求解，

由此可見，在日常的數學教學過程中，教師如果能以數學的本質為起點，看重數學知識點的系統性和整體性，引導學生尋找并理解各個知識點之間的內在聯系和本質規律，使學生以小見大，科學歸納和整合各個課時知識點之間的聯系，就能為更好地培養學生的結構化數學思維創造良好的條件。

二、關注階段性知識結構化設計

為了進一步培養學生的數學結構化思維，教師在日常教學中要重視對階段性知識結構的科學設計，引導學生找出知識本源與學習本源之間的異同點，以達到培養學生遷移抽象知識的能力。

例如在講解“分數的意義”相關知識時，部分學生在應用分數意義的過程中經常出現對不同類型分數的混用問題，例如數量倍數比關系的分數與具體數量分數之間的混用。為了解決這一問題，教師可以為學生詳細講解“五分之三塊”的兩種含義：第一種含義為一塊餅的五分之三;第二種含義為三塊餅的五分之一。利用除法運算法則可以實現對分數意義的進一步拓展。拓展后分數的意義既表示整體與部分的關系，又表示求解的每份數（當求解的每份數不滿1時用分數表示）。

由此可見，教師在實際教學過程中，要引導學生在聯系舊知識的基礎上學習新知識，通過找出新舊知識之間的聯系，使學生以整體性的思維將分數與整數進行有效聯系，以達到深入認識和理解“分數意義”的目的，為后期輕而易舉地解答復雜的分數應用題打下堅實的基礎。

三、關注教材重組結構化設計

首先，要科學合理地重組和整合教材內容，對數學知識結構進行整體性的把握和系統性的講解，以設計出符合學生認知特征和學習能力的教學活動，使得學生對所學知識點有一個深入的拓展和延伸，不斷訓練和提高自身的數學結構化思維，從而提高利用數學知識解決實際生活問題的能力，讓學生體會到數學這門學科的應用價值。

例如教師在講解“簡易方程”相關知識時，為了培養學生的創新思維和數學結構化思維，要避免讓學生使用傳統的四則運算法則對簡易方程進行求解，而是讓學生利用等式性質對簡易方程進行求解。為了實現這一教學目標，教師首先要重視對教學等式性質的講解，讓學生在理解和應用等式性質的基礎上，完成對簡易方程的快速求解。但是在這個過程中，學生難免會遇到形如“c-x=d”的方程，此時，學生可能會無計可施，不好求解。在這樣的情況下，教師要為學生收集和整理含有字母式子的相關練習題，對學生進行專項訓練，不斷地提高學生恒等變形的能力，從而培養學生熟練應用等式性質求解簡易方程的能力，進而加深對“同等變形”這一數學思想的認識和理解。

同時，為了拓寬學生的知識面，提高學生利用不同知識求解簡易方程的能力，教師還要為學生講解利用四則混合運算求解簡易方程的過程，讓學生認識求解方程的兩種方法是相互統一的，而非相互矛盾。例如“甲三角形的面積比乙三角形面積多6cm2，試求解CE的長度”，此時學生就可以運用等式性質對這道題進行求解，求解過程如下：

首先根據題中的條件，列出相應的等式“甲三角形面積-乙三角形面積=6”;然后利用等式性質，在等號的兩邊同時加上丙梯形的面積;最后將等式轉化為“正方形面積-三角形面積=6”，從而快速求解出三角形的面積，進而求出CE的長度。

通過引導學生求解這種類型的練習題，學生對等式性質的應用有了更深入的認識和理解，為培養學生的數學結構化思維提供了有力的保障。

由此可見，教師可以通過關注教材重組結構化設計，引導學生從整體性的角度對知識內部規律進行系統把握。這樣一來，不僅有效突破了原有課時不足的局限和束縛，而且能充分理解和尊重學生的主體地位，在科學設計教學內容的基礎上，讓學生利用原有的認知結構認識和理解新知識，從而發展學生的數學結構化思維。

四、關注階段性復習中教學過程的設計

教師在日常教學中，要根據學生的學習情況和認知能力，在充分考慮學生思維水平差異性的基礎上，以培養學生數學結構化思維為目標，實現對每個單元的復習階段的科學設計，讓學生在實際學習的過程中，將自己已掌握的知識進行重組，訓練利用數學結構化思維深入思考和理解題意的能力，從而提高學生對所學知識舉一反三和融會貫通的能力。

五、結語

綜上所述，為了促進學生智力發展，提高學生的獨立思維能力，教師在構建結構化教學思維的過程中，除了要做好以上四個方面，還要樹立與時俱進的教學觀念，不斷改革和創新結構化教學思維構建方法，以設計出新穎有趣的數學教學活動，不斷激發學生的學習興趣，提高學生的智力水平，使學生的思維品質得到全面培養。

【參考文獻】

孔祥林.小學生數學思維結構化培養策略初探[J].小學教學參考，2019（05）：74.

徐海明.小學數學結構化教學的實踐與思考[J].當代家庭教育，2019（35）.