深度探究　感悟思想

楊裕天

摘 要：數形結合思想是建立在數和形優勢互補的基礎上，抓住數與形之間本質上的聯系，課堂上要緊扣核心問題，引領課堂教學，驅動學生深度學習，注重科學合理結構化教學，讓學生在思想的熏陶、數學文化的滲透中感覺數學的魅力。

關鍵詞：核心;驅動;結構化;數學文化

數和形是客觀事物不可分離的，在教學中我們應發揮數形互補，發揮“數形結合”思想優勢解決好核心問題。以學生為主體，通過主動探究，引導深度學習，進一步凸顯數與形的關系，在回顧展望中形成知識結構，讓數形結合思想成為學生的“好幫手”。

一、緊扣核心問題，引領課堂教學

基于知識的特點和學生的認知基礎，如何巧妙取舍教材？教學的著重點在哪里？如何在活動中體會數與形的關系，感受優越性？緊扣這些核心問題，從引導用“形”解決“數”的問題和用“數”的規律解決“形”的問題來展開教學。

課始口算搶答由淺入深，從算式1+3+5=、1+3+5+7=、1+3+5+7+9=，到算式1+3+5+7+9+11+13+15+17+19+21=。大部分學生從躍躍欲試逐步進入了深思，再由老師進行口答，在對比中引發了認知沖突。以“老師是借助這個圖形快速計算的，你知道怎么看呢？”這個問題，瞬時激發學生的疑問與驚奇，促進學生思考，推進并引領課堂教學。

二、關注問題驅動，促進深度學習

新課標指出：學生是數學學習的主體，問題是數學的核心。在教學中我們適時拋出關鍵的、指向性明確、有探究性的問題。有效地促進學生主動學習，積極思考，構建“數”與“形”的關系，讓學生對知識的理解更有深度，思維更加靈動，也強化了應用數形結合思想的自覺性。

活動一（以數表形）

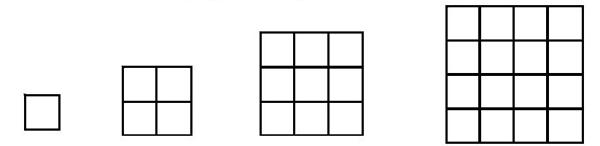
借“11×11的大正方形”為載體，調動學生腦海的知識經驗（化繁為簡），引導從簡單方格中尋找圖形的秘密。出示：

活動要求：用式子或數表示出各方格圖中小正方形的個數。（盡可能多角度思考）

在交流中，學生有用數格子的方法：1個、4個、9個、16個;有用奇數相加：1、1+3、1+3+5、1+3+5+7;還有用乘法表示：1×1、2×2、3×3、4×4;并適時追問：你的算式和圖形是如何對應的？通過表達，及時開啟“數學對話”。學生從不同角度用自己的語言描述時，多次追問，注重學生的學習過程，讓更多的學生在直觀引導下深受啟發，對“數”與“形”的關系有了感悟，知識得到了補充和深化，同時也提升了學生思維的深度和廣度！

活動二（歸納規律）

1=1²1+3=2²1+3+5=3²1+3+5+7=4²

活動要求：仔細觀察四組等式，你有什么發現？

交流中提出：有不同的意見嗎？誰還有發現？等等開放式的問題，并在遷移類推、數學建模環節中繼續追問：“為什么要從1開始？”“非得是奇數嗎”等核心問題，通過數與形結合，初步發現了連續奇數與平方數之間的關系。給出1+3+5+7+9，適時追問：看到這個算式，你心中有形嗎？適時拉近學生心里“數”與“形”的關系，最后通過課件展示有效地構建數與形的關系。在深度“對話”、推理、建模中學生得到了共識。

活動三（變式拓展）

在應用規律練習中1+3+5+7+5+3+1=（? ），注重培養發散思維：有不同想法嗎？一觸即發，除了拆成1+3+5+7與5+3+1，這個解法，還想到了5+3+1=9，將此算式轉化為1+3+5+7+9=52，還有的想到了拆成2個算式1+3+5，再加7，教師及時“退”，在問題的驅動下適時引領學生“進”，促進規律在鞏固中提升，也培養了學生的發散思維。

又如：鞏固應用變式拓展環節，出示1+3+5+…+（? ）=92括號里應該填哪個數？追問：你能用形來解釋嗎？本節課又引向了另一個高潮，引發了更大的“數學對話”，學生紛紛用化繁為簡的思想方法予以一一驗證，課件予以直觀輔助，學生達成共識。繼續追問：如果不是92，是n2呢？括號里應該填什么？規律從特殊到一般化，促進遷移應用，滲透符號化思想，拓展問題維度，進一步促進學生深度學習，有效提升學生素養。

三、注重結構化教學，感悟思想熏陶

布魯納說過：“獲得的知識如果沒有完整的結構與之聯在一起，那么知識多半會遺忘掉。”本節教學的目的不是學生單純地理解某個知識點，或者硬性地提高某一類問題的解決能力，而是學生對數形結合思想有更深的感悟，今后數學學習能自覺應用。故而我們應精心設計教學，結構化整體呈現，讓學生的知識結構有連續性，認知結構有發展性，讓數形結合思想在內心深處扎根！

引導學生回顧我們是如何解決那一道難倒你們的算式？在我們的數學學習中你還能舉出數形互助的例子嗎？學生紛紛舉例：六年級剛學習的分數乘分數、植樹問題、畫線段圖解決問題……最后播放微視頻小學數學數形結合思想的典型實例，并延伸拓展，有效地溝通了這些實例內在本質的聯系，形成知識結構，學生深刻感悟數形結合思想，達到“既見樹木，又見森林”的效果，有效積累數形結合思想活動經驗。

四、滲透數學文化，豐富數學教學

新課標指出：要站在文化角度審視數學，在數學教學中融入數學文化，學生能感受到數學的奇妙，數學的美，感悟數學思想。故而，我們在思考如何安排教學活動時，不可忘記適時融合數學文化，以此讓我們的課堂教學生動豐富，學生在感覺有趣的同時還理解了數學知識的來龍去脈，也一定程度激發了創造力。

課末播放微視頻——在遙遠的古代，以畢達哥拉斯學派為代表的學者們在沒有紙的環境下，研究出了數與形的密切聯系。學生了解到：除了今天學習的“正方形數”，原來還有“三角形數”“正五邊形數”……開闊了視野。之后引用數學家華羅庚關于數形結合的名人名言，學生產生共鳴，親身感受數學文化的魅力！

總之，教師在把握教材時要站在一定的高度，立足好教學目標，以生為本，在課堂上要適時“蹲下”，以關鍵問題來促進學生對新知的理解，讓探究更有深度，讓思維更有維度，教學靈動而豐滿！

編輯 魯翠紅