數(shù)學(xué)教學(xué)在高考中的核心素養(yǎng)分析及反思

摘 要:在我國(guó)教育改革中,強(qiáng)調(diào)了核心素養(yǎng)的重要,在高中數(shù)學(xué)教學(xué)中必須做到核心素養(yǎng)的培養(yǎng),因此相對(duì)的在核心素養(yǎng)下如何進(jìn)行數(shù)學(xué)測(cè)試評(píng)價(jià),也成了教育改革的重點(diǎn)。建立以核心素養(yǎng)為中心的數(shù)學(xué)測(cè)試評(píng)價(jià)需要做到以下兩點(diǎn),第一,分析傳統(tǒng)數(shù)學(xué)測(cè)試評(píng)價(jià),找尋其中的核心素養(yǎng),并以此重新認(rèn)知數(shù)學(xué)測(cè)試評(píng)價(jià);第二,探究新的核心素養(yǎng)下的數(shù)學(xué)測(cè)試評(píng)價(jià)。
關(guān)鍵詞:核心素養(yǎng);數(shù)學(xué)測(cè)試評(píng)價(jià);高中數(shù)學(xué)
一、 引言
在新課程教學(xué)標(biāo)準(zhǔn)中,所提出的核心素養(yǎng),是我國(guó)目前教學(xué)改革中的重點(diǎn)內(nèi)容。這一改革內(nèi)容的提出,為眾多的教師與專家學(xué)者提供了新的挑戰(zhàn)目標(biāo),其中最為重要的挑戰(zhàn)目標(biāo)之一就是如何進(jìn)行核心素養(yǎng)的評(píng)價(jià)。在近些年的教學(xué)改革影響中,高考已經(jīng)進(jìn)行了相應(yīng)的改革,對(duì)核心素養(yǎng)進(jìn)行考查,因此文章將針對(duì)高考中的核心素養(yǎng)考查進(jìn)行分析與反思。
二、 問題提出
在我國(guó)黨的十九大中,明確提出在教育行業(yè)中,必須全面發(fā)展素質(zhì)教育,培養(yǎng)學(xué)科核心素養(yǎng)。在高中教學(xué)過程中,數(shù)學(xué)作為其中的重點(diǎn)學(xué)科,在核心素養(yǎng)的培養(yǎng)過程中具有重要的作用與影響,因此加強(qiáng)數(shù)學(xué)學(xué)科的改革是目前教學(xué)改革與學(xué)校發(fā)展的主要方向之一。核心素養(yǎng)是學(xué)生在數(shù)學(xué)課堂進(jìn)行數(shù)學(xué)知識(shí)學(xué)習(xí)時(shí)逐漸自主形成產(chǎn)生的,這是其思維、能力、情感以及價(jià)值觀的綜合表現(xiàn)。在新課程教學(xué)標(biāo)準(zhǔn)中,指出數(shù)學(xué)核心素養(yǎng)主要包含:數(shù)學(xué)建模、數(shù)據(jù)分析、直觀想象、數(shù)學(xué)抽象、邏輯推理以及數(shù)學(xué)運(yùn)算。并且新課程教學(xué)標(biāo)準(zhǔn),在綜述中指出學(xué)業(yè)質(zhì)量與考試評(píng)價(jià)所具有的重要影響與重要作用,因此在內(nèi)容中直接添加學(xué)業(yè)質(zhì)量這一板塊,在這一板塊中主要講述了核心素養(yǎng),同時(shí)在附錄中,也添加了核心素養(yǎng)的內(nèi)容,提出三個(gè)核心素養(yǎng)的評(píng)價(jià)水平。通過對(duì)新課程教學(xué)標(biāo)準(zhǔn)的閱讀,可以發(fā)現(xiàn)其中眾多的專家學(xué)者都已經(jīng)注意到核心素養(yǎng)的重要性,并且也發(fā)現(xiàn)核心素養(yǎng)評(píng)價(jià)方式的匱乏,因此很多的專家學(xué)者都對(duì)于這一內(nèi)容進(jìn)行了研究與探討,如在《數(shù)學(xué)通報(bào)》中就曾發(fā)布了相關(guān)文章,進(jìn)行相關(guān)內(nèi)容的論述,為很多的專家學(xué)者提供了啟示。在進(jìn)行核心素養(yǎng)的評(píng)價(jià)測(cè)試中,需要教師進(jìn)行重點(diǎn)的設(shè)計(jì),使試題具有更多的形式和排序,設(shè)計(jì)出優(yōu)秀的試題,作為學(xué)生進(jìn)行高中學(xué)習(xí)情況的終極評(píng)價(jià),也作為各高校進(jìn)行人才選拔的重要方式。因此,如何在高考內(nèi)容中實(shí)現(xiàn)對(duì)核心素養(yǎng)的評(píng)價(jià)是目前教學(xué)的重點(diǎn)方向。文章將以核心素養(yǎng)的角度度對(duì)現(xiàn)有的高考試題進(jìn)行分析,分析其對(duì)核心素養(yǎng)的考查情況,并論述其如何進(jìn)行評(píng)價(jià),這也是教師所必須做的任務(wù)。
三、 核心素養(yǎng)視角下的高考數(shù)學(xué)試卷
在進(jìn)行高考試卷分析過程中,主要針對(duì)試卷中各試題中所包含的核心素養(yǎng)進(jìn)行分析,從而探究其評(píng)價(jià)方式與評(píng)價(jià)情況。在高考的試題中,核心素養(yǎng)的具體體現(xiàn),主要可以從以下四個(gè)方面中表現(xiàn)出來(lái),分別為情境與問題、知識(shí)與技能、思維與表達(dá)以及交流與反思。從而根據(jù)這四個(gè)方面進(jìn)行核心素養(yǎng)的評(píng)價(jià),核心素養(yǎng)的評(píng)價(jià)主要?jiǎng)澐譃槿齻€(gè)層次,分別為高中畢業(yè)水平、高考水平以及拓展水平。但是結(jié)合數(shù)學(xué)核心素養(yǎng)源于知識(shí)這一觀點(diǎn),知道核心素養(yǎng)的形成與知識(shí)的學(xué)習(xí)分不開,因此在對(duì)核心素養(yǎng)進(jìn)行評(píng)價(jià)中,也擺脫不了知識(shí)的考查,這種關(guān)聯(lián)關(guān)系,更是將核心素養(yǎng)落實(shí)到實(shí)際中,因此可以將所劃分的三個(gè)層次,進(jìn)行細(xì)致概述,分別為知識(shí)理解、知識(shí)遷移以及知識(shí)創(chuàng)新,這三個(gè)層次的劃分更加精確鮮明。結(jié)合核心素養(yǎng)的六個(gè)方面,可以做出如圖一所示的學(xué)科核心素養(yǎng)評(píng)價(jià)框架。
知識(shí)理解,作為學(xué)科核心素養(yǎng)的第一層標(biāo)準(zhǔn),主要表現(xiàn)為:清晰知識(shí)的來(lái)源;明確知識(shí)的基本;明確其最后結(jié)果。
知識(shí)遷移,學(xué)科核心素養(yǎng)的第二層標(biāo)準(zhǔn),主要表現(xiàn)為:可以簡(jiǎn)單進(jìn)行類比推理,可以運(yùn)用到不同的試題情境中;明確知識(shí)之間的相互聯(lián)系,靈活進(jìn)行知識(shí)的轉(zhuǎn)移;能完成需要多個(gè)知識(shí)結(jié)合的試題,并且能運(yùn)用多種方法。
知識(shí)創(chuàng)新,學(xué)科核心素養(yǎng)的第三層標(biāo)準(zhǔn),主要表現(xiàn)為:具有主動(dòng)探究試題的意識(shí);具有主動(dòng)探究試題的能力;能靈活運(yùn)用所學(xué)習(xí)的知識(shí),解決不同形式的問題;能自主形成數(shù)學(xué)思維。
根據(jù)以上知識(shí)框架,對(duì)高考試題進(jìn)行分析與舉例。
評(píng)析:試題中,主要考查了向量模的計(jì)算,在這一問題中,只需要將向量進(jìn)行化簡(jiǎn)后,直接運(yùn)用向量模公式的計(jì)算,直接進(jìn)行計(jì)算就可以。因此,這一問題主要是對(duì)于知識(shí)的直接運(yùn)用,進(jìn)行直接運(yùn)算,所以屬于知識(shí)理解層次,標(biāo)定為C1。
【例2】 (2020年文考高考全國(guó)卷一第3題)埃及胡夫金字塔是古代世界建筑奇跡之一,它的形狀可視為一個(gè)正四棱錐,以該四棱錐的高為邊長(zhǎng)的正方形面積等于該四棱錐一個(gè)側(cè)面三角形的面積,則其側(cè)面三角形底邊上的高與底面正方形的邊長(zhǎng)的比值為( )
評(píng)析:該問題考查了學(xué)生的直觀想象能力與數(shù)學(xué)建模能力,通過對(duì)試題的分析,提取出其中所存在的等量關(guān)系,通過對(duì)各種特征量假設(shè),在本題中,主要假設(shè)四棱錐的高與底面正方形的長(zhǎng)度,從而運(yùn)用兩個(gè)特征量之間所存在的等量關(guān)系,找出兩者之間的比值。所以在這個(gè)試題中不僅僅是對(duì)于學(xué)生幾何知識(shí)的考查,也需要學(xué)生具有一定的邏輯推理能力,才能在不同的情景中找尋到不同的等量關(guān)系,并最后建立等式解決問題。所以難度屬于知識(shí)遷移,因此標(biāo)定為I2與M2。
(1)求C的方程;
(2)點(diǎn)M,N在C上,且AM⊥AN,AD⊥MN,D為垂足,證明:存在定點(diǎn)Q,使得|DQ|為定值。
評(píng)析:在這問題中,第一問題較為簡(jiǎn)單,直接運(yùn)用公式,建立等量關(guān)系直接可以解答出問題,考查了學(xué)生的邏輯推理能力。在第二個(gè)問題中,就需要學(xué)生直觀想象,運(yùn)用等量關(guān)系進(jìn)行計(jì)算,解決問題。試題中,主要考查了邏輯推理、數(shù)學(xué)運(yùn)算與直觀想象,并且考查難度較大,屬于知識(shí)的遷移,因此標(biāo)定為R2、C2與I2。
在以上三個(gè)高考問題的標(biāo)定過程中,主要借鑒了朱先東和吳增生的標(biāo)定方式。在標(biāo)定過程中,可以發(fā)現(xiàn)高考試題更加具有綜合性,其中考查的內(nèi)容更加全面,在一個(gè)試題中不僅僅考查了某一個(gè)單一的核心素養(yǎng),并且在試題中對(duì)于每一個(gè)核心素養(yǎng)的考查程度也不相同,因此在對(duì)于考查的核心素養(yǎng)標(biāo)定過程中,需要按照其考查的比重進(jìn)行標(biāo)定。核心素養(yǎng)的分?jǐn)?shù)評(píng)定也主要以卷面分?jǐn)?shù)為主,但是由于高考的復(fù)雜程度,需要考查的因素較多,因此在評(píng)定過程中,主要保持總分的不變,以核心素養(yǎng)的比重重新進(jìn)行分?jǐn)?shù)分配,批閱成績(jī)。
四、 核心素養(yǎng)背景下數(shù)學(xué)試題命題嘗試
在我國(guó)的教育改革中,主要是以核心素養(yǎng)作為中心進(jìn)行改革,因此核心素養(yǎng)的測(cè)試評(píng)價(jià)作為其中重要的一環(huán),具有重要的意義,表述了核心素養(yǎng)的落實(shí)情況。在近些年的研究與探討中,眾多一線教師與專家學(xué)者都針對(duì)這一目標(biāo)參與到實(shí)驗(yàn)中,并在核心素養(yǎng)的測(cè)試評(píng)價(jià)工作中取得了一定的成果,同時(shí)在一些高考中已經(jīng)開始了核心素養(yǎng)背景下的數(shù)學(xué)命題嘗試,其中最為代表性的就是在2018年的北京市高考中所出現(xiàn)的。
【例4】 (2018年北京市理科數(shù)學(xué)高考試題第13題)請(qǐng)舉例說明“若f(x)>f(0)對(duì)任意的x∈(0,2]都成立,則f(x)在[0,2]上是增函數(shù)”為假命題的一個(gè)函數(shù)是?
解析:在這個(gè)試題中可以發(fā)現(xiàn),問題的答案不再具有唯一性,學(xué)生也將會(huì)具有更多的發(fā)揮空間,運(yùn)用自己所學(xué)習(xí)的知識(shí),進(jìn)行設(shè)想與聯(lián)想,從而找尋到問題答案。在這一試題之中,考查學(xué)生對(duì)于基礎(chǔ)知識(shí)的理解,并對(duì)其數(shù)學(xué)抽象能力與邏輯推理能力進(jìn)行考查,具有明顯的核心素養(yǎng)考查作用。
在核心素養(yǎng)的基礎(chǔ)下進(jìn)行問題的命制,需要考慮好在問題中所希望進(jìn)行考查的核心素養(yǎng),以及考查的主要群體,所以在問題設(shè)計(jì)過程中,問題的設(shè)計(jì)可以更具有開放性。
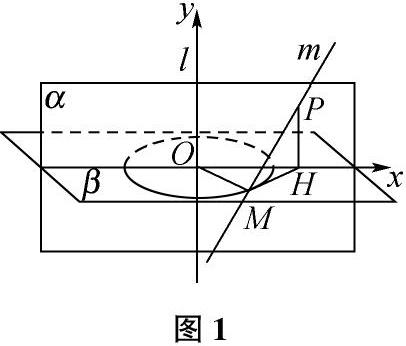
【例5】 直桿如何從彎曲的洞通過?
如圖1,一個(gè)直桿被固定在Г型支架上,放置在桌面上,固定一點(diǎn)O,Г型支架可以繞著點(diǎn)O進(jìn)行旋轉(zhuǎn)。在桌面上存在一個(gè)垂直的面α,請(qǐng)問在平面α上挖出一個(gè)什么樣的洞,才能保證直桿可以正常進(jìn)行旋轉(zhuǎn)。
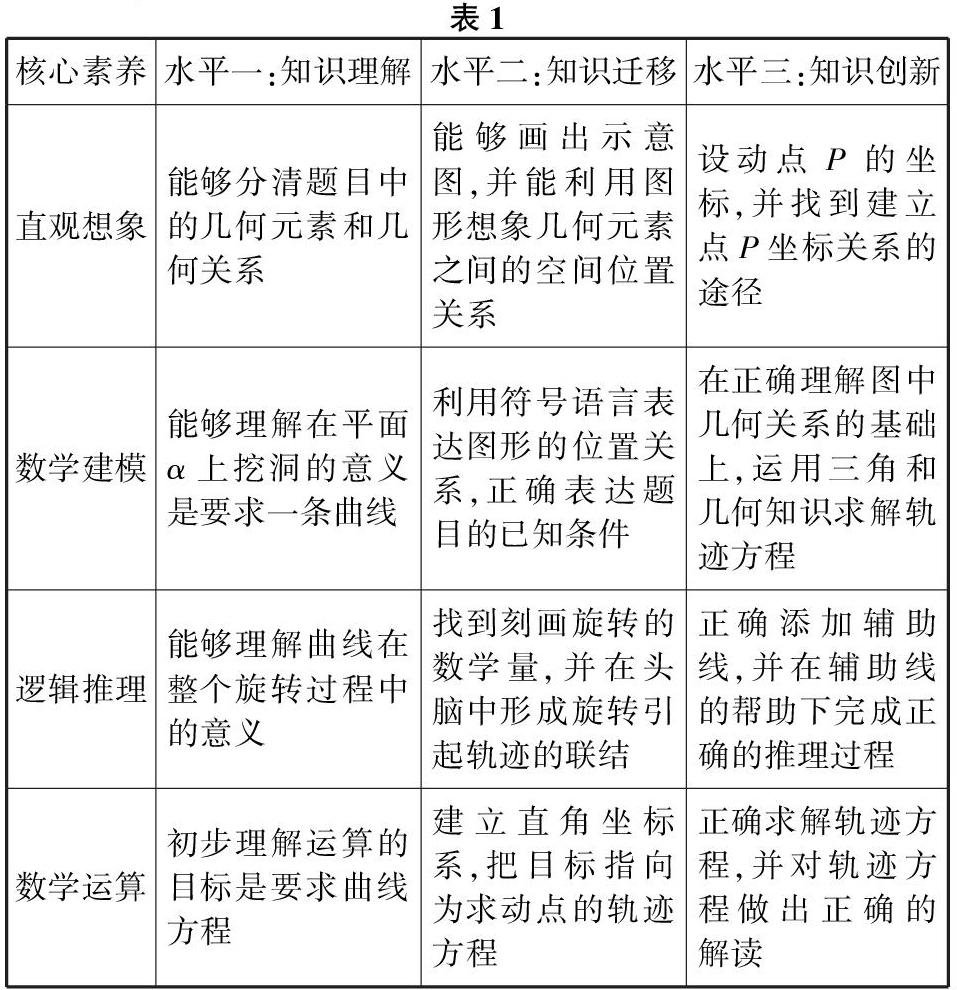
評(píng)析:這個(gè)試題難度過大,不符合各省份的高考試題難度要求。但是這一試題主要是運(yùn)用高中所學(xué)習(xí)的知識(shí),分別為立體幾何知識(shí)、圓錐曲線知識(shí)以及三角函數(shù)知識(shí),因此是學(xué)生可以解決的問題。在整個(gè)問題中考查了所有的數(shù)學(xué)核心素養(yǎng),其中主要考查的是直觀想象、數(shù)學(xué)建模與邏輯推理。并且這一試題的考查,符合了核心素養(yǎng)第三層次的考查標(biāo)準(zhǔn),是一個(gè)優(yōu)秀的知識(shí)創(chuàng)新。在這一試題中具有很多的核心素養(yǎng)體現(xiàn),如表1。
五、 結(jié)束語(yǔ)
在核心素養(yǎng)下的高中數(shù)學(xué)測(cè)評(píng),是一個(gè)需要教師不斷探索的內(nèi)容,在現(xiàn)有的評(píng)測(cè)基礎(chǔ)上積極探索,進(jìn)行改良與完善,形成更具核心素養(yǎng)特點(diǎn)的測(cè)評(píng),其中通過2018年的北京卷與2020年的全國(guó)一卷都可以發(fā)現(xiàn)。在這兩份試卷的分析過程中,也能發(fā)現(xiàn)高考中的數(shù)學(xué)試卷也逐漸趨向于對(duì)數(shù)學(xué)本質(zhì)的考查,引導(dǎo)學(xué)生探究數(shù)學(xué)的美感,這一試題在每個(gè)時(shí)刻都不會(huì)被淘汰。所以這一改革方向也為教師提供了新的挑戰(zhàn),教師應(yīng)把握機(jī)會(huì),展示自身才能,為數(shù)學(xué)學(xué)科的發(fā)展做出努力。
參考文獻(xiàn):
[1]何金祥.探析核心素養(yǎng)的考查形式和要求:以2019年浙江數(shù)學(xué)高考試卷為例[J].求知導(dǎo)刊,2019(37):2-4.
[2]劉剡.核心素養(yǎng)視閾下數(shù)學(xué)高考試卷研究[D].南昌:江西科技師范大學(xué),2019.
[3]王國(guó)軍.注重?cái)?shù)學(xué)運(yùn)算,提升核心素養(yǎng):以2018年全國(guó)高考數(shù)學(xué)試題為例[J].中學(xué)數(shù)學(xué),2019(3):34-36.
[4]鄧迎春,張曉飛.高考中的數(shù)學(xué)核心素養(yǎng)問題[J].中學(xué)數(shù)學(xué),2018(11):31-33.
作者簡(jiǎn)介:
黃榕鑫,福建省福州市,福建省福州第七中學(xué)。

