借助數學問題培養小學生數學思維的路徑分析

商欽平

摘 要：思起源于疑。有了疑問，才能促使學生積極思考，自覺主動探究。而小學數學作為基礎學科，數學學習的本質就是不斷思考的過程。所以在教學中要注意課堂提問的藝術性，通過不同問題的設置，激發學生的積極性，拓展學生的思維，提高教學效率。

關鍵詞：小學數學;問題導學;數學思維

亞里士多德說過：“思維自問題、驚訝開始。”問題是激發學生思維的原動力。在數學課堂中，課堂提問是把學生、教師、教材緊密聯系起來，它是培養學生學習興趣、引導學生深入思考、檢驗學生學習情況的有效途徑。有趣的數學問題會鍛煉學生的思維能力，培養學生多方位思考能力，課堂氣氛活躍，主動參與學習。因此教師應懂得以問導學，以問啟智，把問題貫穿于數學教學始終，這是提高數學思維能力的有效途徑。

一、 趣味性的問題，營造思考的欲望

托爾斯泰說過：“成功的教學所需要的不是強制，而是激發學生的興趣。”學習興趣是產生學習動機的源泉，是促進學生深入主動學習的動力。學生年齡還小，結合教材特點和學生實際情況，一個情境，一個問題，就把學生帶進了探索知識的海洋，想去揭開知識神秘的面紗，想去分析、思考、解決，變“要我學”為“我要學”。

比如：在教學“約分”時，筆者出示圓片問：“誰能在1分鐘之內涂出這個圓片的75100？”學生個個躍躍欲試，有的學生奮筆疾書，馬不停蹄地想完成教師的任務;有的學生冥思苦想，定要找出教師葫蘆里賣的啥藥;有的學生滿臉喜悅，信心十足……通過這樣的比賽，學生表示驚奇和困難，呈現出濃厚的興趣，讓學生進一步理解分數的基本性質，感受應用價值和約分的好處，激發學生學習的興趣。在課堂中，都要學會利用素材和資源，挖掘學生感興趣的切入點，讓學生在輕松快樂的狀態下激發思維潛能。

二、 操作性的問題，激發提問的內驅力

小學生以形象思維為主，教師應多提供學生“做”的機會，因為只有自己真正動手操作、實踐、觀察、思考，才能對知識深層次地理解，以便更好地掌握知識，做到觸類旁通。教學中，教師應當盡可能提供增強感性認識的機會，在不斷地演示操作中，引發矛盾，提出問題，促進思維。

比如，在教學《植樹問題》時，學生猜測：當兩端都栽時，棵樹比間隔數多1。教師追問：“你怎么知道？”學生建議：“畫圖解釋更直觀，一圖解千愁呀！”學生發愁了：“100米數據太大了，怎么畫？”學生炸開鍋了：“可以化繁為簡”“選多少米呢”“20米、35米、30米、15米……”學生激烈地討論，組長有序地安排不同的數據各自驗證，得出了共同結論：當兩端都栽時，棵樹比間隔數多1。是啊，通過動手實踐中存在的問題，不斷激發他們的提問意識，主動探索問題，自己尋求解決的方案，從而結論水到渠成。

三、 探究性的問題，實現深度思維

直來直去的問題，單調無趣，缺乏啟發性，無法拓寬學生的思路，很難調動學生的積極性。而新時代要求學生要有創新性，能夠從多種角度思考問題，不單局限于單一模式，這就要求教師在課堂上多設置探究問題，讓學生的思維向更深層次拓展，充分培養創新思維的能力。

比如，在初步學習分數比較大小后，出現了這樣的一道題（如下）。

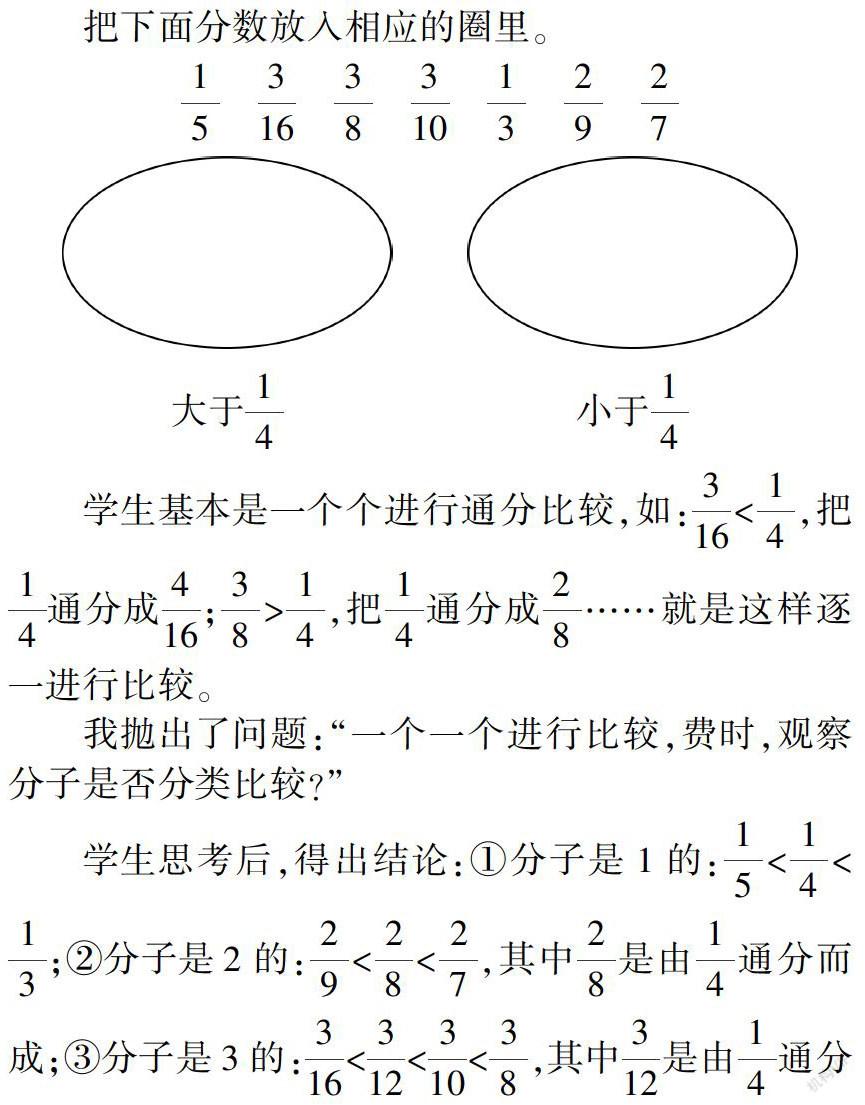
把下面分數放入相應的圈里。

學生基本是一個個進行通分比較，如：316<14，

把14通分成416;

38>14，把14通分成28……就是這樣逐一進行比較。

我拋出了問題：“一個一個進行比較，費時，觀察分子是否分類比較？”

學生思考后，得出結論：①分子是1的：15<14<13;

②分子是2的：29<28<27，其中28是由14通分而成;

③分子是3的：316<312<310<38，其中312是由14通分而成。一個問題引發思考，分類整理，不僅省時，而且思維清晰、條理性強。

四、 開放性的問題，強化發散的思維

學數學要想辦法激活學生的思維，引導他們學會創造性地思考，而開放性的問題不僅可以鞏固基礎知識，還可以引導學生多角度探究、交流與合作，以便深化和擴展知識。所以在教學中應該有意識地設置開放性問題，關注條件的多種呈現，解決問題步驟方法的多樣性和結果開放的程度。讓學生從各自身有的認知基礎出發，積極參與其中，親身去體驗、建構自己的認知。

比如，在教學《分數大小的比較》綜合練習中，按分數的大小從小到大排列：

45，1112，

43，710，12，

56。學生建議：“可以把這些分數全部進行通分，這樣就能比較大小了”。問題出來了：“這么多的分母如何找出它們的最小公倍數。”學生開始沉默了，過了十幾秒，有學生開始發言：“6和3是12的因數，2和5是10的因數，我們只要找出10和12的最小公倍數就一定是這些分母的最小公倍數。”“有道理，用它們的最小公倍數60通分能解決啦！”正在學生沉浸在成功的喜悅時，筆者又拋出了一個問題：“如果不通分能否解決這題呢？”有學生就開始思考了，接著：“其中43最大，因為它是假分數，其他都是真分數。”“12是最小的，因為其他的數都比一半多。”“剩下的數看看誰跟1最接近，如，45差1個15，1112差1個

112……”就這樣用學生的話來說：“不用計算，我竟然看都能看出它們的大小，我們太厲害了！”有的學生開始疑問：能不能把這些分數都化成小數來比較呢？“是啊，小數和分數的互化將是下節課要學習的內容，到時就能用你提議的方法解決了！”問題的開放，且給學生有足夠的思考空間，不但牢固地掌握基礎知識，還拓寬了思維的深度和廣度，得到了許多意想不到的精彩。

五、 生活性的問題，提升應用的能力

現實情境是數學學習進行發展的基礎。數學的教學也需要從現實角度來實行。學生在掌握知識的同時，也要學會以變通的思維方式來解決現實問題，感受學有所用。因此，教師在教學中，努力滲透生活思想，創設生活性問題，體驗數學知識的價值，激發學生應用能力的發展。