智慧教育云平臺下《折疊問題》導(dǎo)學(xué)案教學(xué)設(shè)計課例

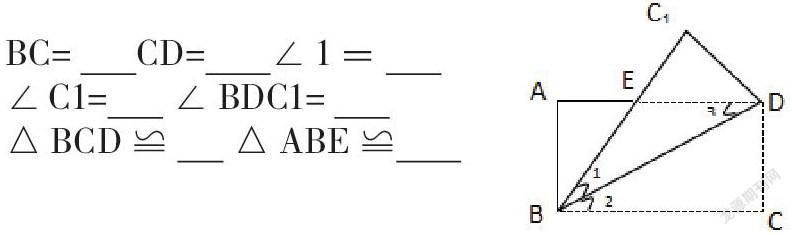
【摘要】專題課是中學(xué)階段數(shù)學(xué)學(xué)習(xí)的重要課型，旨在突出章節(jié)重點、突破教學(xué)難點.教師在選材、教學(xué)設(shè)計、課堂把控等環(huán)節(jié)要注重以學(xué)生為主體，在教學(xué)過程中切忌將知識直接“丟”給學(xué)生，以免學(xué)生產(chǎn)生厭倦心理 ，而是應(yīng)該創(chuàng)設(shè)合理有趣的教學(xué)情境，讓知識自然生成，讓問題迎刃而解，從而生成一節(jié)生動有趣的“新型專題課”.本文以《折疊問題》這一專題課為例，筆者創(chuàng)設(shè)了一個折紙的情境，讓學(xué)生在折紙游戲中發(fā)現(xiàn)并解決折疊問題，很好的踐行了“新型專題課”這一理念.教學(xué)時，筆者采用“導(dǎo)學(xué)案”的教學(xué)模式，以問題鏈形式激發(fā)學(xué)生學(xué)習(xí)興趣和好奇心，一張A4紙不同的折疊方式帶來的不同的問題，引發(fā)學(xué)生自主觀察、發(fā)現(xiàn)、提問、探究、解決，從而培養(yǎng)學(xué)生多方面的數(shù)學(xué)能力，發(fā)展學(xué)生的核心素養(yǎng).

【關(guān)鍵詞】折疊問題;導(dǎo)學(xué)案;教學(xué)設(shè)計

一.教學(xué)意圖

1.本節(jié)課主要結(jié)合了四邊形的性質(zhì)與判定及此前學(xué)的三角形全等、勾股定理等知識解決折疊問題，折疊變換在幾何問題中的應(yīng)用較為廣泛，方程思想貫穿始終，主要培養(yǎng)學(xué)生通過動手實踐解決數(shù)學(xué)問題的能力，同時發(fā)展數(shù)學(xué)建模、直觀想象、邏輯推理等核心素養(yǎng).

2.鼓勵學(xué)生手腦并用，切身體會動手解決數(shù)學(xué)問題的樂趣.

3.深度融合信息技術(shù)，利用智慧教育云平臺輔助教學(xué).

二.教學(xué)目標(biāo)

1.知識目標(biāo)：通過一題多變解決以矩形為背景的折疊問題，領(lǐng)悟方程思想、轉(zhuǎn)化思想、數(shù)形結(jié)合等重要數(shù)學(xué)思想;

2.能力目標(biāo)：在變式教學(xué)中培養(yǎng)觀察發(fā)現(xiàn)、動手實踐、邏輯推理和數(shù)學(xué)表達能力;

3.素養(yǎng)目標(biāo)：在解決變式問題及折紙游戲中發(fā)展直觀想象、邏輯推理、抽象概括、數(shù)學(xué)建模等核心素養(yǎng).

三.重點、難點

重點：在折疊問題中求解線段長;

難點：找到解題的切入點.

四.教學(xué)過程

（一）課前導(dǎo)學(xué)——折疊感知

將矩形ABCD沿對角線BD折疊，點C的對應(yīng)點為點C1，C1B交AD于點E，請口答下列問題.

【教師活動】

啟發(fā)：根據(jù)等量傳遞性或三角形全等發(fā)現(xiàn)等量關(guān)系.

設(shè)疑：為什么會有這些等量、全等關(guān)系？

【學(xué)生活動】

1.課前填寫：完成導(dǎo)學(xué)案中【課前導(dǎo)學(xué)】任務(wù).

2.課堂回答：個人回答【課前導(dǎo)學(xué)】問題.

【設(shè)計意圖】

1.【課前導(dǎo)學(xué)】在知識生長點設(shè)問，符合學(xué)生知識生成規(guī)律，容易激發(fā)學(xué)生學(xué)習(xí)興趣，避免畏難情緒.

2.以問題為載體，學(xué)生活動為主線，讓學(xué)生的思維“動”起來.

3.在折疊動態(tài)中解答數(shù)學(xué)問題，發(fā)展學(xué)生直觀想象的核心素養(yǎng).

（二）回顧真題——重溫經(jīng)典

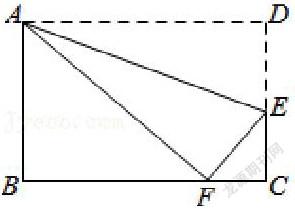
如圖所示，將長方形ABCD沿AE折疊，頂點

D恰好落在BC邊上F處，已知CE=3，AB=8，則

BF=

【教師活動】

概括：回顧解題過程，總結(jié)解題思路.

設(shè)疑：能否提煉出折疊問題中求線段長的解題思路？

【學(xué)生活動】

1.齊答：回顧真題解題過程.

2.獨答：提煉折疊問題中求線段長的解題思路.

【設(shè)計意圖】

1.讓學(xué)生在熟悉的情境中回顧解決折疊問題的思路，為后續(xù)變式問題做鋪墊.

2.檢驗學(xué)生對于已經(jīng)講過題目的熟知程度，提醒學(xué)生溫故知新.

3.發(fā)展學(xué)生抽象概括、邏輯推理等核心素養(yǎng).

（三）一題多變——舉一反三

【變式1】

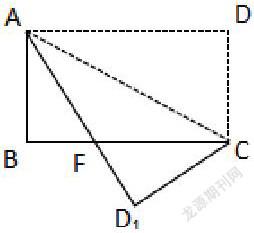
如圖所示，將長方形ABCD沿AC折疊，使得點D落在點D1處，BC交AD1于點F，AB=8，AD=10，求FC.

【教師活動】

激勵：鼓勵學(xué)生板演.

【學(xué)生活動】

1.獨立思考：獨立審題，積極思考.

2.學(xué)生板演：板演解題過程.

3.生生互評：邀請學(xué)生評價板演過程.

【設(shè)計意圖】

1.鼓勵學(xué)生規(guī)范書寫，在解題過程中再次體會折疊問題求線段長的基本思路，發(fā)展學(xué)生邏輯推理、數(shù)形結(jié)合等核心素養(yǎng).

2.一題多變，改變真題中的折疊方式，引導(dǎo)學(xué)生找到不同折疊方式的解題切入點，突破教學(xué)難點.

3.以生生互評的評價方式來培養(yǎng)學(xué)生的表達能力.

【變式2】

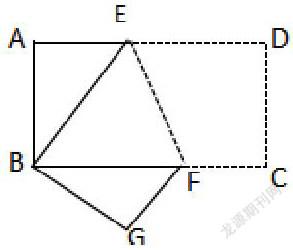
如圖所示，將長方形ABCD沿EF折疊，使得點D落在點B處，點C落在點G處，AB=8，AD=10，求△BEF的面積.

【教師活動】

探索：在此問題中關(guān)鍵是求出哪條線段長？

評價：生生互評.

【學(xué)生活動】

獨立思考：獨立審題，積極思考.

交流互補：同桌之間交流討論.

成果展示：邀請學(xué)生代表上臺講解.

生生互議：為什么求線段BF的長？

【設(shè)計意圖】

1.一題多變，當(dāng)折疊方式和求解問題都變的情況下，引導(dǎo)學(xué)生發(fā)現(xiàn)問題本質(zhì)仍為“求線段長”，突出重點知識的活用.

2.在不同的折疊情境下體會不同問題的解題方式，領(lǐng)悟轉(zhuǎn)化、方程、數(shù)形結(jié)合等重要思想.

3.生生互議，暴露學(xué)生思維，挖掘解題思路.

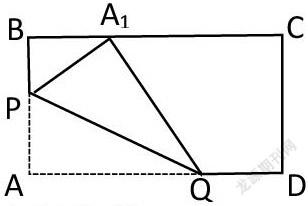
【變式3】如圖所示，AB=8，AD=10，點P、Q分別在線段AB、AD邊上移動，將長方形ABCD沿PQ折疊，使點A落在BC邊上的A1處，當(dāng)點A1在BC邊上移動時，點P、Q也隨之移動，則點A1在BC邊上可移動的最大距離為多少？

【教師活動】

引導(dǎo)：利用課前準(zhǔn)備的A4紙來進行實際演練.

演示：教師利用雙色A4紙進行實際操作展示.

展示：利用投屏技術(shù)，將學(xué)生游戲的過程展示在大屏幕上.

【學(xué)生活動】

獨立思考：獨立審題，積極思考.

實驗操作：折疊A4紙，探索從直觀上解題.

交流互補：小組之間交流討論，合作實踐.

成果展示：每組邀請兩名學(xué)生合作展示.

【設(shè)計意圖】

1.營造“探究場”，把課堂還給學(xué)生，鼓勵學(xué)生通過合作交流展示想法， 去動手操作，讓學(xué)生的思維“火”起來 .

2.將“動點問題”與“折疊問題”相結(jié)合，培養(yǎng)學(xué)生用數(shù)學(xué)實驗解決問題的意識及動手實踐能力.

3.引導(dǎo)學(xué)生手腦并用，將操作與思維相結(jié)合掀起課堂高潮，讓學(xué)生在學(xué)中玩，在玩中學(xué).

（四）數(shù)學(xué)游戲——減負增效

【折紙游戲—減負增效】

能否在不借助工具的情況下，利用一張A4紙做出一個等邊三角形？

【教師活動】

展示：利用投屏技術(shù)，將學(xué)生游戲的過程展示在大屏幕上.

微課：植入微課視頻解說折紙方法.

分享：成功作品.

設(shè)疑：能不能證明所折三角形是等邊三角形？

【學(xué)生活動】

交流探究：學(xué)生找到同伴進行探究.

成果展示：展示學(xué)生作品.

【設(shè)計意圖】

1.引導(dǎo)發(fā)現(xiàn)而不奉送知識，把握方向而不限制學(xué)生，把發(fā)現(xiàn)的“樂趣”留給學(xué)生.

2.寓教于樂，進行折紙游戲，感受到數(shù)學(xué)好玩有趣，做到減負增效.

3.用微課突破游戲難點，讓學(xué)生模仿微課介紹的方法折紙，把操作方法的理性證明留到課后，給學(xué)生留下探索的懸念.

（五）歸納小結(jié)——畫龍點睛

構(gòu)建知識網(wǎng)絡(luò)，引導(dǎo)學(xué)生從知識、方法兩方面出發(fā)，梳理重難點內(nèi)容.

【學(xué)生活動】

交流：學(xué)習(xí)收獲.

分享：心得體會.

【設(shè)計意圖】

畫龍點睛，構(gòu)建知識網(wǎng)絡(luò).

（六）課后作業(yè)——減負增效

必做題：

教材77頁A組習(xí)題.

選做題：

（1）教材79頁C組習(xí)題.

（2）嘗試證明本節(jié)課游戲環(huán)節(jié)的問題.

【學(xué)生活動】

寫題：鞏固重點知識，熟練解題步驟，梳理知識體系.

【設(shè)計意圖】

分層作業(yè)，減負增效.將課內(nèi)知識延伸到課外，設(shè)計有趣的課后作業(yè)，激發(fā)學(xué)生創(chuàng)造性思維.

參考文獻：

[1]導(dǎo)、學(xué)、議、評、練、悟——學(xué)案導(dǎo)學(xué)六步教學(xué)模式芻議[J].易斌.名師在線.2021（01）

[2]“授人以漁”的同時“授人以漁與欲”——以《等差數(shù)列的前n項和》公式推導(dǎo)片段為例[J].唐劍嵐，周元.數(shù)學(xué)通報.2016（09）

作者簡介：郝圓，廣西桂林，大學(xué)本科，桂林市第十八中學(xué)教師.