高中數學課堂教學中數形結合思想在函數解題中的應用探究
林秋萍
◆摘? 要:函數是高中階段的重要組成,具備內容繁多、邏輯性強、抽象性強的特征,學生對于函數題的解答較為困難,再加上教師的教學思維模板化,學生難以靈活運用多種思想迅速解決函數題。因而,教師要靈活化教學策略,在教學中積極融入數形結合思想,實現“數”與“形”之間的靈活轉化,讓學生學會將復雜問題簡潔化,將抽象的函數直觀化,進而快速找到解題突破口,有效解決函數題。基于此,本文就數形結合思想在高中數學教學的運用意義展開論述,提出了其在函數解題中的有效運用,學生能夠快速、有效的解決函數類問題。
◆關鍵詞:高中數學;數學結合思想;函數解題
數形結合思想的關鍵在于“數”和“形”的靈活轉換,讓學生將抽象的函數通過畫圖直觀地呈現出來,在經過觀察、分析后,快速找到突破口。因此,數形結合思想作為普遍、常用的數學解題思路,教師在傳遞學生數形結合思想時,應該注重探究,加強講解,讓學生有效實現“數”和“形”之間的靈活轉化,讓學生真正學會應用數學,實現學生思維能力、知識應用水平的全面提升。
一、高中數學課堂教學中數形結合思想在函數解題中的應用意義
高中數學的函數題型相對于初中的教學內容和難度進一步提升,其計算和思考過程更為繁瑣,學生難以把握其規律和特征,以致于無法有效解決。如在函數題型中,大多都是不常見的函數類型,學生在面對這些例題時往往無從下手,不會將函數問題轉化成圖像問題,進而無法有效解決。因此,如果學生不具備“數形結合思想”,則將會對其的解題效率帶來極大影響。其次,數形結合思想是一種注重轉化的思想,具備較強的靈活性,能夠幫助學生解決多種綜合性較強的函數題,在數和形之間來回切換,最終找到問題的突破口。最后,數形結合思想強調構圖,即將數字信息轉化為圖像信息,學生對問題的探究將會更加直觀化,通過數形結合思想的運用,賦予學生靈活變通的思維方式,學會從多角度看待問題,其創新思維也在此過程中形成。因此,如果學生不具備“數形結合思想”,仍是采用傳統的解題手段,則會極大限制學生的思維,最終影響解題效率。
二、高中數學課堂教學中數形結合思想在函數解題中應用的不足
當下高中數學中仍然存在“灌輸式”教學,存在一定的盲目性和形式性,即使部分教師滲透數形結合思想,也通常表現為一帶而過,學生無法掌握其內涵,具體而言,在應用數形結合思想中存在問題主要表現在以下幾個方面:首先,教師一味的講解教材知識,忽略了對教學的內容的拓展和變通,缺乏對數學思想的導入意識。其次,沒有深刻意識到數形結合思想的重要性,只停留在簡單的數和形的互譯。最后,教師缺乏構圖意識,難以為學生呈現出良好的數形轉換講解,以致于學生遇到問題時,不能在第一時間想到利用數形結合思想解答。
三、高中數學課堂教學中數形結合思想在函數解題中的應用策略
1.發揮出教師的引導作用,深刻踐行數形結合思想。高中數學的函數知識對于學生而言需要較強的理解和觀察能力,在運用數形結合思想時,首先要讓學生在探究過程中自行探索、自行思考,教師只是作為引導者或者解惑者,通過教師引導和學生自主探究,有效實現數形結合思想的滲透。所以在數形結合思想灌輸時,老師要循序漸進的引導,不能直接告訴學生答案,或者告訴學生采用何種思維,而是在教師的引導下一步步的找出突破口,讓學生有跡可循。例如給出一個三角函數例題:cosx+2sinx=,求tanx的值。這種題目是數學中較為常見的例題,具有一定的代表性,所以教師就可以很好的利用這道題進行數形結合思想的滲透,由于cosx和sinx的內容和其他的計算數值不等同,所以在加法中可以利用一些簡單的字母進行換元處理,在極短的時間內化繁為簡,然后借助于坐標圖迅速找出正確答案。
2.選擇典型例題,培養學生的思維能力。高中數學中包含了眾多典型函數例題,教師要借助于這些典型例題讓學生帶著數形結合思想進行解答,培養出他們獨立思考能力和知識運用能力。
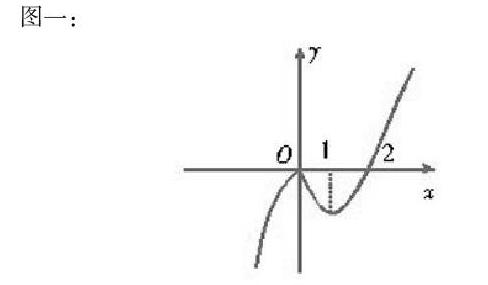
3.注重構圖,實現對圖形和函數的綜合分析。在函數類例題中,教師要引導學生遵循數形結合思維,讓學生學會構圖,通過直觀的觀察坐標圖結合函數的類型,迅速解決問題。例如在函數f(x)=值域求解時,要根據函數內容進行坐標圖繪制,將抽象的函數轉化為斜率范圍中的數學問題,進而快速獲取答案。此外,數形結合思想也可用于正弦、余弦求解,如在求正弦、余弦值時,可以在角終邊線取一點P(1,y),在RT三角形PAO內,AO=1,此形況下P(1,y)為,這類函數圖通過畫圖化輔助線的方式,能夠輕松得出答案。此外,數形結合也可用于單調區間問題,如一函數為確定y=x丨x丨-2丨x丨的單調區間,畫出函數草圖(如圖一),直觀得出答案y=x丨x丨-2丨x丨=x?-2x,x≥0或者-x?+2x,x<0,快速得到單調遞增區間為區間為(-∞,0],[1,+∞)。單調遞減區間為[0,1]。
四、總結
數形結合思想是數學學習中最為基本、也是最為重要的思維方法,借助于“數”和“形”的轉化,將復雜的函數問題直觀化,讓學生能夠巧妙解答。因此,教師要深刻意識到數形結合思想的重要性,在課程教學中加強引導,在教學中經常性地構圖,將數和形的核心運用根植于學生的腦海,讓學生具備多樣性、靈活性的思維,在解決函數類問題時首先想到的就是數學思維。
參考文獻
[1]張小瑜.高中數學課堂教學中數形結合思想在函數解題中的應用探究[J].高考,2020(08):151.
[2]賀有銘.高中數學課堂教學中數形結合思想在函數解題中的應用探究[J].高考,2016(15):147-148.

