自主合作探究學習方式與高中數學教學的有機結合

張樹華

摘 要：伴隨新課改的普及深入，對高中數學教學提出更高要求。為保質保量完成教學目標，需要數學教師摒棄傳統觀念，積極改善教學方法。自主合作探究學習方式的運用，不僅能激發學生興趣，促進學生思考，還能幫助學生在探索中找出數學規律，理解數學內涵。因此，需要將自主合作探究學習方式引入數學課堂。本文就如何在數學課堂有效實施自主合作探究教學進行探討，以供廣大同仁參考。

關鍵詞：高中數學;自主探究;合作學習

前言：數學是高中階段的基礎性學科，蘊含諸多概念定理，學生理解起來著實不易。再加上學生正值思維發展階段，各項能力均有所欠缺，無法準確把握數學知識。當前不少教師課堂教學急于求成，重完成，輕過程，通用灌輸式的教學方法，不僅效率低，效果也難以達到預想。甚至會讓學生心生畏難情緒，心生抵觸，從而拒絕學習數學，失去數學學習興趣，欲速則不達。在培養學生核心素養的大環境下，傳統教學方式不利于學生素質提升，需要進行革新。自主合作探究學習方式是一種新穎的教學手段，可轉換師生角色，對提升學習效率很有幫助，因此，本文從自主合作探究學習方式的價值入手，對自主合作探究學習方式的應用策略進行探索，旨在促進學生思維品質的形成和良性發展。

一、自主合作探究學習方式在高中數學教學中的應用價值

（一）激發學習興趣

以往數學學習，學生大多單兵作戰，不僅學習難度大，還容易積累問題。伴隨時間推移，問題越積越多，學生內心就會產生自己不行的想法，從而對數學學科失去興趣，產生畏懼感。常言道：“興趣是學習的推動力。”唯有讓學生對數學產生興趣，他們才會自主開展探究活動[1]。設置問題是激發興趣的有效手段，能讓學生對教學活動滿懷期待。同時，借助數學懸念可讓學生感知到數學學科的魅力所在。

（二）培養合作意識

傳統課堂中教師作為主導，學生只能被動的接受知識，不僅學習效率不高，合作意識也會欠缺。合作學習模式，會將學生分為若干小組，每組中有一名小組長，負責統籌協調學習任務。組內成員之間會相互幫助，共同完成學習目標。

（三）轉變師生角色

在新教學模式中，教師不再是主導者，而是引導者。在整個教學過程中，教師要細心觀察，掌握每一位學生的表現，并結合學生的學習需要及時調整教學方針。在數學課堂，教師會發現有些學生表現出似懂非懂的神情，這是學生心中產生疑惑的表現。教師還能發現在發言階段有些學生交頭接耳，說明這位學生有不一樣的想法。有的學生會欲言又止，說明學生尚不確定自己的想法等等現象，教師要及時捕捉學生的這些特殊狀況，有效幫助學生解決困惑，推動自主合作探究學習活動的有序開展。

（四）促進思維發展

觸類旁通是高中生必須具備的一項技能，而這項能力的形成需要經過千錘百煉[2]。數學問題的解決方法并不單一，角度不同，解決思路不同。在合作學習過程中，學生思維會發生碰撞，從而產生多種解題思路。在思維交流中，學生會有種茅塞頓開的感覺。

二、自主合作探究學習方式在高中數學教學中的具體應用

（一）在概念課中的應用

數學學科蘊含大量的概念，但由于這些概念比較抽象，導致學生無法準確把握。在解決問題時，學生的思路較為混亂。數學概念并非針對個別對象，而是體現相似事物的本質特征。為培養學生科學認知，需要應用自主合作探究學習方式。以《數列的概念》為例，闡述如何開展教學活動。

第一步，創設教學情景，激發學生興趣。教師在大屏幕上呈現一則故事，故事名為“五猴分桃”。到了桃子豐收的季節，5只猴子將桃從樹上摘下，放在一起。第1只猴子嘗試分桃，分好后發現還剩1個。它認為自己付出勞動，桃子理應歸自己，隨即吃了這個桃子，抱著屬于自己那份桃子就走了。第2只猴子并未看到之前那一幕，以為桃子還沒有分，隨即投入到分桃大業中。最后發現剩下一個，它選擇將其吃掉，也抱著一堆桃子離開。后面來的猴子，不斷重復這個過程。待學生閱讀完，教師問學生：最初有多少桃子？最后這一堆有多少桃子？學生紛紛陷入沉思。這時，教師問：“你們想知道答案嗎？”學生說：“想。”見學生已經進入學習狀態，教師則進行下一步。

第二步，合理分配小組，推進自主探究。眾所周知，學生個體存在差異，學習水平有高有低。為保證合作探究有效果，需要教師合理劃分小組。教師要掌握學生學情、了解學生興趣特點，盡可能讓各小組的實力均衡。待分組完畢后，教師布置學習任務。任務1：自行閱讀課本，并找到這些問題的答案。（1）數列概念中的關鍵詞都是什么？（2）數列的一般形式是什么？a1是數列的第幾項？an被稱作數列的什么？（3）將表格內容補全，見表1。（4）在特殊情況下，可將數列看作是一類函數，定義域是什么，成立條件又是什么？

任務2：以小組為單位探討問題。（1）2，4，6，8，10和10，8，6，4，2是不是相同數列？（2）{an}與an有何區別？（3）假設an=n（n-2），其中n∈N+，請說出{an}的第五項、第九項、第十一項分別是什么。（4）請寫出1，2，4，8，16，32...的通項公式。

學生在探究學習中難免會遇到問題，先由學生自行解決，如若解決不了，再由教師答疑解惑。對于共性問題，教師在課堂上解決。對于個性問題，教師可在巡視中發現并指導或私下解決。在教師的正確引導下，學生將問題全部解決，說明學生已基本掌握數列概念。

第三步，巧設練習題目，鞏固所學知識。教師要精心準備練習題目，以此加深學生記憶。習題1：觀察四個選項，判斷其是否屬于數列，并闡述理由。A.2，4，6，8，10;B.6，5，2，3，4，7;C.1，3，5，6，7，2;D.6，14，2，13，7，9。習題2：判斷這兩種說法的對錯，并陳述理由。A.所有整數均可以構成數列;B.{1，3，...，2n-1，2n+1}屬于無窮數列范疇。習題3：寫出這三個數列的通項公式。A.2，5，8，11，14，17...;B.3，33，333，3333....;C.1，2，1，2，1，2，...。待學生解答完畢后，以小組形式進行討論，并各小組選派一名學生說明習題答案。最后，由教師總結本堂課的主要內容。

（二）在定理課中的應用

數學知識之間有著千絲萬縷的聯系，而數學定理最大的作用就是揭示這種關系[3]。定理不會隨著時間推移而發生改變，是數學教學的核心所在。受傳統思想束縛，很多教師采取講解方法，無法讓學生領略其中奧秘，導致學生不能準確運用。為扭轉這個局面，需要實施自主合作探究學習。以《正弦定理》為例，闡述如何開展教學活動。

第一步，巧妙設置問題，激發學生欲望。教師在屏幕上展示情境創設，內容是有一個三角形，其有三個頂點，分別為A、B、C。假設將BC邊和∠B固定住，而AC邊圍繞C點做旋轉運動，請問∠C大小和AB邊長度之間是否存在某種關系？如若存在，這種關系又是什么？學生閱讀完題目后，會在本上畫出草圖。對照草圖，進行思考。經過思考后，仍找不出答案。此時，學生的好奇心被激發。當學生進入學習狀態后，教師即可開展下一步工作。

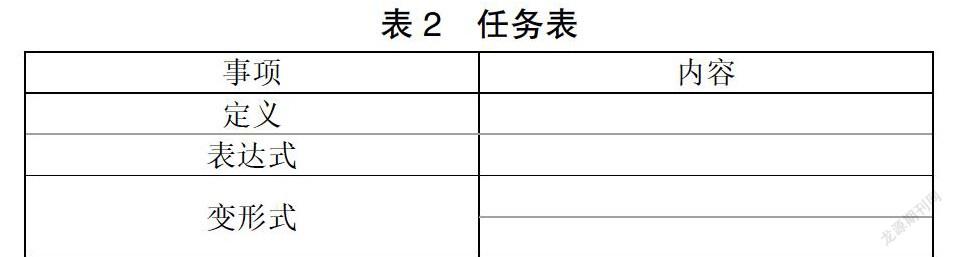
第二步，回顧已學知識，推導正弦定理。教師先幫助學生回憶直角三角形知識，主要圍繞邊角關系展開。當然，邊角關系的變形方式也要進行總結。待學生記憶被喚醒后，教師提出一個問題，即變形式是否適用于其他三角形？由學生推導答案。這個過程中，教師只負責巡視監督與指導。待學生解答問題后，教師讓學生填寫表格內容。

第三步，布置課堂練習，加深學生理解。當學生填寫無誤后，說明學生已基本掌握定理，這時就可借助習題加深理解。問題1：任何三角形都符合正弦定理要求嗎？問題2：在△ABC中，sin∠A>sin∠B，∠A所對邊也會長于∠B所對邊，這種說法是否正確？如若不正確，請說明理由。問題3：假設某個三角形中兩邊長度和一個角的角度（并非這兩邊夾角），請說出這個三角形一共有多少個解？為提升解題效率，教師要組織合作學習。在思維碰撞中，學生的認知逐漸完善，對正弦定理的把握更加準確。

（三）在復習課中的應用

復習課的主要目的是回憶已學知識，梳理知識架構，最終達到融會貫通。受限于方法老舊，導致復習效率不佳。為徹底解決這個問題，需要運用自主合作探究學習方式。借助該模式加深學生理解，促進完整架構的形成。以數列復習課為例，闡述如何運用該教學方法。

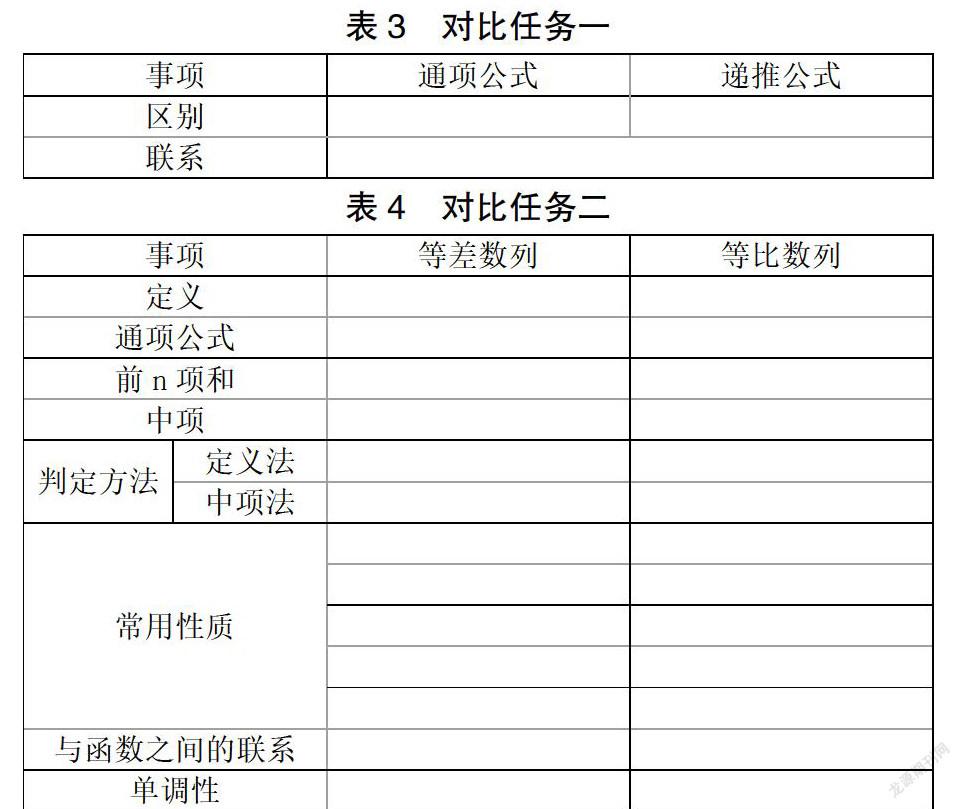
第一步，明確復習內容，推動合作學習。按原先劃分小組，完成回顧這幾方面內容：一是數列概念，包括定義、通項公式、遞推公式、前n項和公式、數列的分類、數列的函數刻畫。二是探討區別，見表3、表4。

第二步，精心準備習題，增強學生認知。待喚醒學生的回憶后，教師需準備一些習題鞏固知識基礎。習題1：已知{an}是一個數列，其前n項和為Sn=2n-1，求an。習題2：{an}是等差數列，{bn}是等比數列，a1與b1均為1，a2加a4等于b3，b2乘以b4等于a3，請分別計算{an}和{bn}的前十項和。習題3：已知f1（x）=2x-1，f2（x）=x2，{an}的前n項和等于f2（n），{bn}的b1為2，bn等于f1（bn-1），請給出{an}的通項公式，并通過驗證獲得一個結論，即{bn-1}是等比數列。

第三步，鼓勵學生發言，歸納解題技巧。當習題解答完畢后，教師要組織學生進行總結。鼓勵學生大膽發言，分享解題技巧。教師將方法一一列出，并歡迎學生補充。只有學生掌握更多的方法，才能又快又好的解決問題。當然，同一種方法不一定適用不同人，學生要根據自身情況進行選擇。

結語

在新時期下，傳統數學教學弊端日益突出，不利于學生的素質發展，因此需要數學教師及時調整思路，創新教學模式。自主合作探究學習方式一經問世就備受關注，是數學教學改革的有力助手。教師將其應用在方方面面，幫助學生準確理解數學概念定理，全面掌握數學規律。長此以往，學生的數學綜合能力就會養成，這對其今后的發展至關重要。

參考文獻

[1]楊娟娟.合作學習在高中數學課堂上的應用[J].才智，2020（05）：61.

[2]陳小娟.論高中數學高效課堂的構建[J].亞太教育，2019（07）：86.

[3]馮洪濤.高中數學教學中學生合作學習開展方法探究[J].科學咨詢（教育科研），2019（11）：178.