實施有效探究培養思維能力
葉艷當


[摘 要]“綜合與實踐”是引導學生進行高效能的數學思維活動,提升學生的數學核心素養的有效途徑。文章以人教版教材一年級下冊的“綜合與實踐”活動的“擺一擺,想一想”為例進行課例探究,通過層層遞進和形式豐富的探究活動,幫助學生理解數位和位值的概念知識,激活學生的數學思維,培養學生的思維能力。
[關鍵詞]數位;位值;有效探究;數學思維
“綜合與實踐”是學生積累數學活動經驗的重要載體,能使學生的思維得到不同層次的發展。以一年級下冊中的“擺一擺,想一想”為例,實施“以學為中心,以探為重點”的課堂教學模式,通過操作擺圓片,讓學生在“擺一擺、想一想、說一說、寫一寫、辨一辨”的多元探究活動中厘清數位和位值的概念,經歷知識的形成過程,提升數學素養。
一、基于問題所在,激活思維支點
筆者先對學生(總人數:50人)進行前測,具體情況如下表:
最大的數是(? ?),最小的數是(? ?) 能有序完成的 5人 10% 30% 無序完成的 10人 20% 數據有遺漏的 20人 40% 60% 數據有重復的 10人 20% 完全不會做的 5人 10% 10% ]
大部分學生都能猜出題意,只是不能準確寫出所有的數,主要是因為學生解題的思維還處于混亂、無序的狀態,對知識的綜合應用能力較低。為此,筆者把握本課的思維支點,準確定位,以幫助學生從無序、混亂、膚淺的思維意識走向有序思考、發現規律、解決問題。
1.分析教材,弄清教學意圖
基于以上問題,本課教學(如圖1)有四個主要環節:
環節1.引導學生用2個圓片擺出不同的數,知道每個圓片在每個數位表示不同的位值,感受“位值”的概念。
環節2.引導學生利用3個圓片有序擺出不同的數,做到不重復、不遺漏地準確地擺出,初步滲透有序思維。
環節3.引導學生利用4個、5個及更多個的圓片擺出不同的數,發現并歸納規律“圓片的個數+1=擺出數的個數;十位和個位上的數相加的和等于圓片的個數”,學會運用規律有序、快速、準確地寫出所有擺出的數。
環節4.利用10個圓片幫助學生擺脫規律的局限性,展現推理過程的嚴密性,培養學生的科學精神。
2.深挖聯系,明確目標定位
本課的支點是一年級上冊的“分與合”。學生在“分與合”的學習中已經體驗了有序思考的方法,只是相隔時間較長,學生不能有效聯系新舊知識,產生思維斷層,而且對于不同數位上的數所表示的意思處于理解不清的狀態。為了解決這一問題,筆者引導學生運用類比遷移的方法感悟數位表的位值概念,培養學生的有序思維,也為二年級上冊“搭配”的學習做鋪墊。
二、厘清抽象概念,找準思維入口
數學概念往往是抽象的知識,而低年級學生以形象思維為主,較難理解抽象的數學邏輯,教師需借助圖像、操作等動態演示,幫助學生形成相應的數學知識表象,建立相應的數學概念。筆者設計了兩個不同層次的探究活動,通過活動,借助有效的提問引發學生思考,幫助學生初建表象。
1.溫故導新,抽象概念
由于數位和位值概念較為抽象,筆者把數位和位值概念的理解層面定在對各個數位表示的意義上,即個位表示幾個一,十位表示幾個十。
首先,出示數位表(如圖2),引導學生回顧數位表的相關知識點,如把1個圓片放在十位上表示1個十,也就是10;把1個圓片擺在個位上,表示1個一,也就是1。用1個圓片擺在不同的數位上表示不同的數,能直觀有效地幫助學生厘清數位及位值的概念,為學生發現數的特點和規律打下基礎。
其次,讓學生利用2個圓片擺數。學生通過操作學具,就能夠理解抽象的知識,為后續學習奠定基礎。
最后,要求學生利用畫圓的方式記錄思考過程,脫離學具輔助,逐漸把具體操作過渡到符號方式,提升符號意識和抽象思維能力。(如圖3)
2.重在探究,經歷優化過程
隨著圓片個數的增多,擺出的數會相應增多,學生的正確率會相應降低,因此有序擺法最為關鍵。學生用3個圓片擺數時,出現了以下情況(如圖4):
第一種:較為零亂,出現遺漏。
第二種:可以完整寫出所有的數,但雜亂無序。
第三種:個位和十位互換,出現遺漏。
第四種:能有序擺數,做到不遺漏、不重復。能按從大到小的順序擺,即把所有圓片放在十位上,再把圓片一個一個地從十位挪到個位上,擺出的數越來越小;也可以按從小到大的順序擺,即把圓片都放在個位上,再把圓片一個一個地從個位挪到十位上,擺出的數越來越大。
在匯報交流中,學生對比各種方法,發現第四種方法是最優的:有序地擺數能完整地寫出所有的數,不容易出現混亂、遺漏或重復的現象。
通過以上活動,學生經歷了“漏寫—完整寫—有序寫”的知識探究過程,優化了解題方法,鞏固了畫圖的記錄方法,初步認識了有序地擺數。
三、實施有效探究,培養思維能力
數學思維過程是一個抽象化的過程,教師要巧妙地適時點撥,引導學生將知識類比遷移,激活學生的思維方式,提升學生的數學綜合能力。
1.靈活轉換,助力思維提升
為了讓學生能夠運用規律解決實際問題,教師就要引導學生發揮想象力:在大腦中刻畫數位表的模型,想象用4個圓片能擺幾個數,利用類比遷移的方法寫出4、13、22、31、40,或者40、31、22、13、4。此時,教師無須引導學生發現規律,而是讓學生快速寫出5個圓片能擺出哪些數。由于有前面的表象支撐,學生很快就寫出了50、41、32、23、14、5,或者5、14、23、32、41、50,再根據數據的特點,發現和總結規律,即個位和十位上的數字之和等于圓片的個數,擺出的數的個數與圓片個數相差1。
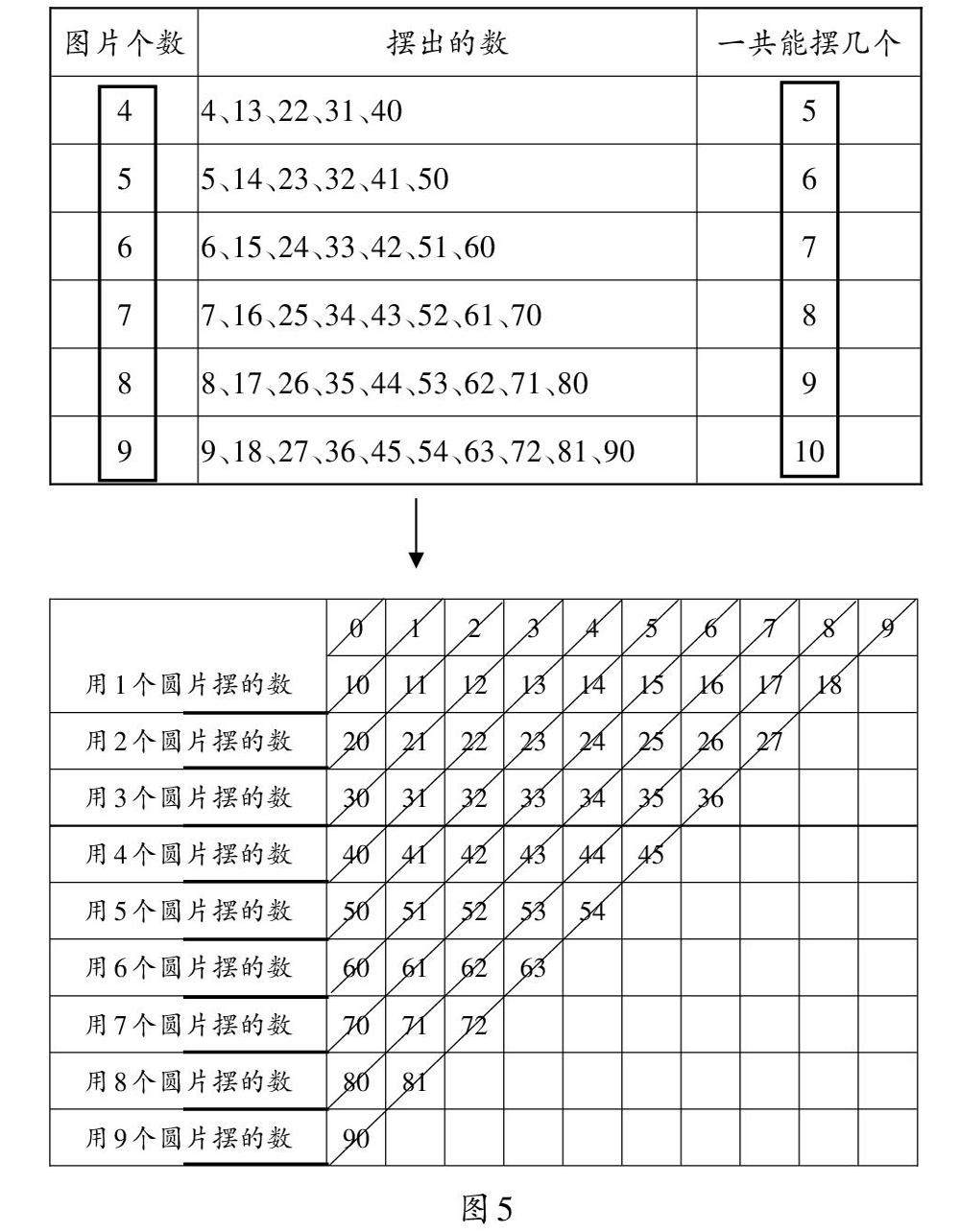
為了加深學生對結論的理解,教師可要求學生利用規律驗證4個圓片和5個圓片擺出的數,并說出6、7、8、9個圓片分別能擺出哪些數。最后呈現百數表時,學生驚喜地發現今天所擺的數是百數表中的一半(如圖5),這樣就有效地融合了新舊知識,學生感受到知識之間的密切聯系,增強了數感。
通過想一想、辨一辨,學生發現規律、驗證規律,思維得到進一步的提升。如果說前期的規律發現是學生自發產生的直覺,而后期的師生驗證和總結則是一個聚焦規律的過程,這個過程可以使學生對規律和結論的認識更深刻,從而有效發展學生的推理能力和概括能力。
2.適度拓展,完善思維深度
練習是重要的驗證環節,通過不同層次的訓練,能提升學生的綜合應用水平,使不同層次的學生得到發展。低年級學生對解析密碼很感興趣,對此,可設計一道拓展題:
本題沒有提示學生這個數是用10個圓片擺出來的,而是讓學生根據第2個提示“十位和個位數字相加,和是10”,推理出這個數是用10個圓片擺出的,再根據第3個提示,學生先認為密碼就是100,但很快就否定了,因為第1個提示已明確“密碼是兩位數”,而100是三位數,不符合條件。學生很快就想到另一個數——99,但99的個位和十位之和是18,并不是10,不滿足第2個提示……學生在“推理—推翻—再推理”的思維碰撞中,得出滿足條件的數只有91。
此時,教師可讓學生反思:10個圓片能擺出哪些兩位數?根據前面的方法,學生先寫出100、91、82、73、64、55、46、37、28、19、10共11個數,再利用規律檢查后發現100是三位數,不是兩位數,并且100不是用10個圓片擺成的,而是用1個圓片擺成的,因為把1個圓片放在百位上,擺出的數就是100,由于10也不是10個圓片擺成的,從而不能全部用上10個圓片,因為個位滿十要向十位進1,十位滿十要向百位進1,每個數位上最多只能填到9,10個圓片只能擺出9個數。
學生在運用規律解決問題的過程中,感受到:當圓片個數不足10個時,圓片的個數+1=擺出的數的個數;當圓片個數等于10個或超過10個時,需把不符合要求的數從總個數中去掉。這樣,學生經歷了完善規律的過程,感受到數學的嚴密性。
綜觀整節課,“擺”是學生學習抽象知識的具體操作,是建立表象的有效途徑,而“想”是對知識本質的思考和內化。教師需多鉆研教師用書,尋找教學支點,溝通知識聯系,設計有效活動,幫助學生經歷知識的形成過程,提升學生的數學素養,提高學生的數學思維能力。
[ 參 考 文 獻 ]
[1] 曹培英.跨越斷層,走出誤區[D].上海:上海教育出版社,2018:158.
[2] 李小春.《擺一擺 想一想》課例研究[J].小學教學設計,2014(5).
(責編 金 鈴)

