挖掘數學文化 踐行學科育人

王洋洋

[摘? ?要]基于核心素養的學科育人，必須抓住課堂主陣地，從課堂設計的細節入手，關注知識的由來，講透問題的本質，才能實現從知識本身到學生思維方式的轉化，真正達到學科育人。文章通過對一節示范課的片段呈現和點評來闡述學科育人的教學策略。

[關鍵詞]學科育人;核心素養;數學文化;數系擴充;復數概念

[中圖分類號]? ?G633.6? ? ? ? [文獻標識碼]? ?A? ? ? ? [文章編號]? ?1674-6058（2021）30-0031-02

《普通高中數學課程標準（2017年版）》指出，要強調數學與生活以及其他學科的聯系，提升學生運用數學知識解決實際問題的能力，同時注重數學文化的滲透，不斷引導學生感悟數學的科學價值、應用價值、文化價值和審美價值。 當核心素養明確與“必備品格”和“關鍵能力”聯系在一起時，那就意味著學科育人已經不只是德育的專利，而應該更多地以課堂學科教育這個主陣地為契機。其中，數學作為初高中教育的基礎學科，數學教師也應該主動承擔起提升學生智力、滲透文化、培養學生素養的責任，潤物細無聲地達到學科育人的目的。

復數的出現對于力學、電學和其他學科起到極大的推動作用，知識上它可以與平面向量、三角函數密切聯系。更多意義上，它的應用并不像實數系一樣跟我們的日常生活息息相關、觸目可及。復數系更多抽象地存在于科學研究中，可以說它的出現是人類理性思維在數系擴充中的充分體現，是利用實數系中的類比進行抽象、推理而得來的數系。

如何能夠上好《數系的擴充和復數的引入》這堂課，實現學科育人的目標呢？本人有幸參加了南寧三中特級教師黃河清老師召開的高中數學學科育人研究課暨成果總結會，聽到了陳華曲老師關于《數系地擴充和復數的引入》的示范課，現截取幾個片段，做以下思考。

[片段一]概念引入由情景導入，精準把握數學史料的“廣度”和“深度”

由于復數系本身的抽象性，一些“重結論、輕來由”的教師可能會單刀直入講復數的概念形式[z=a+bi] 及復數加減乘除計算，忽略了對虛數單位[ i]的引出，導致有的學生對于虛數系突兀地出現感到莫名其妙，一頭霧水。可以說這樣的做法錯過了一次非常好的讓學生了解數學發展史的機會，委實可惜。因為學科育人育的對象是學生，育的目的是培養學生的數學學習能力，這能力的培養中就應該包括對數學學科歷史的認識。知史以明鑒，查古以至今，學生學習數學前輩攻堅克難的品質，才能勇敢地踏上征程，推動人類數學研究的巨輪繼續前行。

關于“數系發展”的數學史資料非常豐富，如果教師講得太多，一來影響教學進度，二來喧賓奪主，易脫離課堂主題。陳老師并沒有采用一個個故事串聯的方式進行講解，而是收放自如地在浩瀚的數學史料中取其所用。陳老師結合PPT展示數的發展史，利用圖片展示來講解數系的擴充歷程。板書內容：自然數集N→整數集Z→有理數集Q→實數集R。考慮到有的學生理解虛數有困難，陳老師力圖創造構建新概念的心智條件，使學生先形成對新數系的感性認識。學生通過PPT的展示可以得到結論，當數的發展不能滿足人類的使用需求時，就到了要擴充數系的時候。正如恩格斯所說：“數學像所有別的科學一樣，起因于人們的需要。”數系發展的歷程體現了人類探索世界、認識世界的歷程。陳老師水到渠成地講明白了數系擴充的必要性。

當我們在實數系內無法找到[x2+1=0 ]根時，該如何解決這個數學問題呢？陳老師適時拋出這個問題，引導學生像數學家一樣去思考，此時竟然出現了實數系內不能解決的問題，學生自然有興趣去探究新知。

引入新事物——虛數單位[i]，規定[i2+1=0]。

對于虛數單位[i]，值得一提的是，為何要用[i]這個字母，而不用其他的字母？陳老師在課堂上講述了這個史料。萊布尼茨曾經說過：“虛數是神靈遁跡的精微而奇異的隱蔽所，它大概是存在和虛妄兩界中的兩棲物。”正由于它沒有實體存在，所以有個有趣的簡稱，用“imagine”（想象）的首字母[i]表示，所以虛數可以說是“幻想之數”。學生聽后恍然大悟，會心一笑。學生親身體會到數的“發現”與“發明”過程，整個授課過程不拖沓煩冗，陳老師精準地把握了史料的“廣度”和“深度”。

[片段二]數系擴充中“規則”意識的強調必不可少

如果沒有運算，那么數只是孤立的符號。在講授復數概念后，陳老師開始引導學生去探求數系擴充中的“規則”。她提問：“數系擴充后，在運算上遵循什么規則？”所謂的規則，其實就是大學《近世代數》中提到的數系對加減運算各種算子的封閉。找出“規則”是本節課的難點。學生對于規則的歸納用了較長的時間，本人聽課時覺得陳老師在此處的提問有些抽象，可能可以更具體地引導學生。

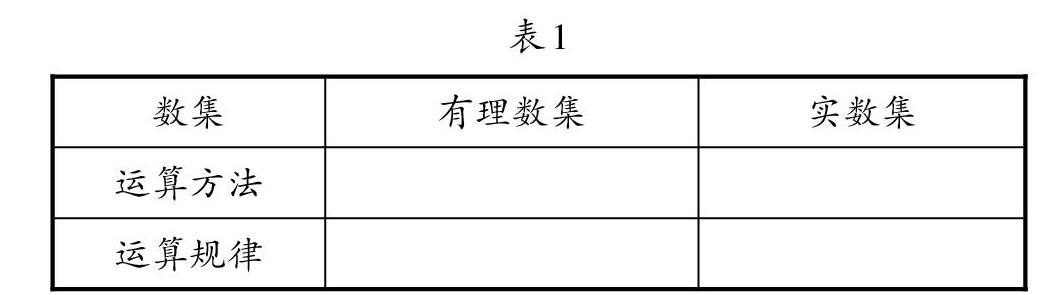
比如，以有理數集在引入無理數之后擴充到實數集為例。可以引導學生小組學習填寫表1。

有了表1的指向性，在該教學環節中學生得出如下表2的答案就不太困難。

陳老師引導學生得到結論：數系擴充后，在新數集中規定的加減乘除運算與原數集中規定的加減乘除運算協調一致，并且加法和乘法都滿足交換律和結合律，乘法對加法滿足分配律。

在“規則”的指導下，學生也考慮到使得方程[x2+1=0]有解，從而可以像實數一樣進行加減乘除，成功地將實數系添入虛數之后擴充為復數系。在尋找這個“規則”時，循循善誘的提問和啟迪過程讓學生體會類比的數學思想，培養了學生的邏輯推理和抽象概況能力。

在教學過程中讓課堂變成學生勇于“嘗試”的課堂，通過學習“活動”讓學生感受知識的奧秘，這就是黃河清老師“三環耦合”的育人模式通過“思維育人、史料育人、審美育人、活動育人”四個維度加強學科育人的集中體現。

如何讓核心素養落地生根，讓學科育人落實到課堂？本人認為，只有這種精雕細琢的課堂設計，教師把握好授課的各個環節、各個維度才能真正實現學科育人，否則核心素養的培養很容易落為空談。

[片段三]條理清晰地對數系歸類

有了虛數單位后，陳老師引導學生自己根據“規則”自由地舉例子。學生利用“規則”指引，大膽發言，給出了如下多個復數的例子。

實數：5、2、1、0

新數：[i ]

利用“規則”自由組合得到的復數：[5+2i]、 [2+5i]、[5i]、[i]、0

觀察多個復數例子，陳老師提問：能否將這些復數寫為一個統一的形式？這是對學生數學抽象概括能力的考查。核心素養是教育界的熱門話題，但是如何判斷學生是否具備高中數學的六大核心素養呢？比如六大核心素養中的“抽象概括”素養，它具隱性且不易衡量，如果學生能夠用語言表達概括出復數的代數形式可以統一寫為[z=a+bi]，并能夠給出合理解釋時，我們就有充分理由相信學生具備這一素養。

“如何根據形式特點對數系歸類？”陳老師又抓住契機提出了新問題。

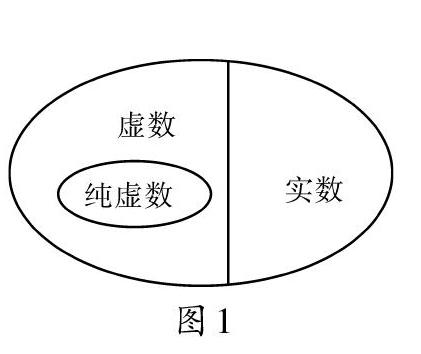
學生陷入思考，不一會兒，陳老師展示了學生畫的venn圖，并解釋自己的分類標準，如圖1所示。

該生的表現非常精彩，贏得在場老師的嘖嘖稱贊。數學語言、文字語言、圖形語言的轉化該生運用得游刃有余，非常熟練。

然后師生合作，填寫分類結果。

復數[z=a+bi實數b=0虛數b≠0純虛數（a=0，b≠0）非純虛數a≠0，b≠0]

最后，陳老師讓學生試著從知識、方法、數學思想、經驗等方面談談本節課有哪些收獲。除了知識層面外，學生還談到數學家也曾有不易解答的難題。小小的[ i] 經過了兩個世紀的努力才被世人所接受。我們只有跳出原有的舊框架，勇敢地“更新觀念”，才會發現更為廣闊的數學天地。

整個課堂中，陳老師都讓學生感受到數學家就在自己的身邊。從發現i，到在“規則”的指導下順利擴充數系，并對數系進行歸類整理，體驗與數學家一起“發現問題→思考問題→解決問題”的過程。

總之，教師只有專注教材的每個細節，立足課堂，精準把握學生的起點、困難和需求，給予正確的指導和幫助，敢于放手、善于引導，讓學生自由表達，并對學生耐心啟發，浸潤、激勵和引導學生，才能真正地以本學科的特質為載體來達到學科育人的目的，實現學生的自我成長。

（責任編輯? ? 黃諾依）