春風化雨潤心田

楊柳

摘 要：數學學科是一門高度抽象、邏輯嚴密的自然科學，本身就蘊含了豐富的思想性。數學課堂中的德育應以理服人，要考慮教材的體系和特點，顧及學生的實際情況，注意教育的策略性和可行性，要善于挖掘教材中的德育、情感因素，將數學教學與德育工作有機結合在一起，潛移默化，從而達到“春風化雨潤心田”的效果。

關鍵詞：德育;數學教學;案例設計

德育是構建德智體美勞全面培養的教育體系的重要組成部分，在落實立德樹人，培育時代新人中發揮著舉足輕重的作用，德育一體化建設是落實國家教育戰略，培養全面發展的人的重要基礎。《普通高中數學課程標準》明確指出：數學教育承載著落實立德樹人的根本任務，發展素質教育的功能。在平常的教學中，我們要緊密結合數學學科教學內容，使德育與智育、體育、美育等有機融合，從而實現全科育人的目的。下面，我就以“兩點間的距離”為例，來說一下我是如何進行德育一體化設計的。

一、借助適當的情境創設，激發學生的學習熱情，培養他們愛學習、愛科學的興趣

數學學科雖然不像文科知識那樣生動活潑，富有情趣，但只要我們抓住數學學科的特點，創設好的學習情境，也能激發學生的學習興趣，達到滲透德育的目的。

以課堂引入這個環節為例，我們可以采用靈活多樣的情境引入，來喚起學生學習的熱情。考慮到上一章我們剛剛學過立體幾何的有關距離，而下一節學生又將接觸到點到直線的距離，所以本節課我采用了知識情境引入，從而幫助學生構建有關距離問題的完整知識體系。

師：說到距離，在我們數學中有很多種，你知道都有哪些？

師：在這么多距離中，哪種距離是最簡單的距離？

（此處教師稍微停頓，讓學生思考，然后學生回答，教師再進行歸納總結即可。）

師：點到點的距離是最簡單、也是最重要的一種距離，因為其他所有的距離都可以轉化為點到點的距離來解決。這節課我們就來學習這種最簡單也是最重要的距離。

這樣的情境引入，是根據數學知識之間的聯系、發展與變化來創設的。它讓學生明白了這節課的基礎性和重要性，培養了學生愛學習、愛科學的興趣。

二、借助數學知識和思想方法，培養辯證唯物主義世界觀

較其他學科而言，數學無論是知識，還是思想方法，都蘊含著極其豐富的辯證法思想，這也是數學學科的一大特點。比如：待定系數法反映了已知與未知的矛盾轉化過程，反證法、補集方法是否定之否定規律的體現;數列、指、對函數等教學內容反映了認識事物從特殊到一般的認知規律。下面以推導兩點間的距離公式這一環節為例，來進行說明：

[問題1]數軸上兩點間的距離公式是什么？

[問題2]如果在直角坐標系中，在x軸上有兩點P1（x1，0）和P2（x2，0），那么點P1和P2之間的距離為多少？如果P1P2平行于x軸呢？

[問題3]在y軸上有兩點P1（0，y1）和P2（0，y2），那么點P1和P2之間的距離為多少？如果P1P2平行于y軸呢？

[問題4]已知x軸上一點P1（x0，0）和y軸上一點P2（0，y0），那么點P1和P2之間的距離為多少？

[問題5]已知平面上任意兩點P1（x1，y1）和P2（x2，y2），那么點P1和P2之間的距離又為多少？

師：勾股定理是數學中解決度量問題最重要的一種方法，除了兩點間距離的推導，后面將要接觸的點到直線的距離，圓的弦長和切線長，以及空間直角坐標系中的距離問題，都會用到勾股定理來推導。

（此處是為了向學生滲透應用勾股定理的意識，讓學生體會勾股定理的文化價值，激發學生的民族自豪感。）

[問題6]你能說出數軸上兩點間距離公式和平面上兩點間距離公式的聯系和區別嗎？

[問題7]你能試著大膽猜測空間中兩點間的距離公式嗎？

（這個探究體現了“未知到已知”“由特殊到一般”“數與形”的相互對立與統一，讓學生學習用辯證的觀點來分析解決問題。）

總之，在教學中，適時地、恰當地滲透辯證唯物主義思想教育，不僅有利于學生對數學知識的深刻理解和對數學方法的熟練掌握，更有助于學生形成良好的思維品質和科學的世界觀。

三、利用數學的學科特點，培養學生善于思考、勇于創新的科學精神

數學中的很多問題都具有相似性和可遷移性。所以，在日常教學中，我喜歡通過一組組變式訓練，引導學生揭示數學問題的本質，幫助學生構建系統的知識體系。比如：在本節課中，我沒有簡單地“就題論題”，而是對例題進行變式訓練，這樣能使學生更深刻理解兩點間的距離公式，培養學生的探索精神和創新能力。

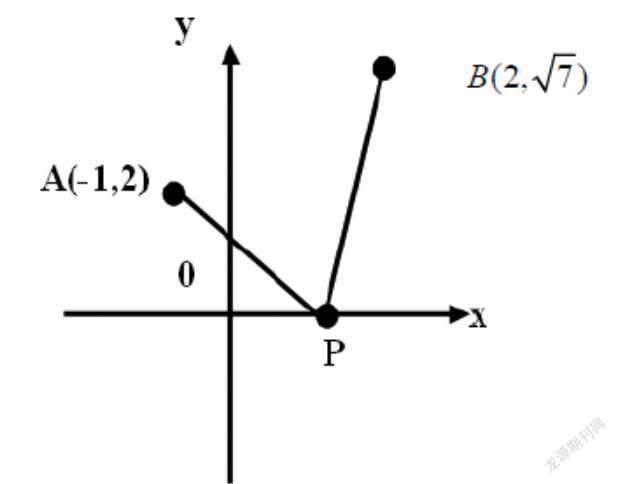
[例1]已知點，在x軸上求一點P，使，并求|PA|的值。

[變式1]如果在y軸上呢？

[變式2]如果在直線y=2x+3上呢？

[變式3]已知點，若，求點P的坐標滿足的方程。

[變式4]在x軸上求一點P，使得|PA|+|PB|取最小值。

（例題和前兩個變式是對在平面直角坐標系中，求點的坐標這一類問題的研究;變式3屬于求軌跡方程問題，為后面學習求曲線方程做好鋪墊;變式4是屬于利用對稱知識求最值問題。這組變式通過不斷變換例題的條件，引深拓展，使一個題目延伸出三類問題，喚起了學生的好奇心和求知欲，培養了思維的創新性。）

數學教育家波利亞曾形象地指出：“好問題同某種蘑菇有些相像，它們都成堆地生長，找到一個以后，你應當在周圍找找，很可能附近就有好幾個。”恰當合理的變式訓練，不僅能產生觸類旁通、舉一反三的學習效果，而且有利于培養學生的應變能力，開闊學生的思路，培養學生的創新能力，形成“以不變應萬變”的能力，從而終生受用！

四、借助探索重難點知識和了解數學史，培養學生嚴謹認真、勇于挑戰困難的優秀品質

（一）探索重難點知識

人的一生總會遇到困難和挫折，對困難和挫折的承受能力是立足于當今復雜多變世界的必備能力。因此，培養學生遇到困難，勇于克服和頑強拼搏是很有必要的。對于難度較大的數學題目，學生在解決過程中，如果不具備堅定的信心、頑強的毅力，是很難解決的。本節課的難點是利用坐標法來證明幾何問題，因此我借助這組探究題，來培養學生知難而上的優秀品質。

[探究]證明：矩形四條邊的平方和等于兩條對角線的平方和。

師：本題能不能利用初中學過的幾何法來進行證明？

師：能不能利用坐標法來證明？

（此處的矩形因為兩條相鄰的邊互相垂直，所以學生無論是建系，還是設點，都能很快解決，教師也及時給予肯定與鼓勵，培養了學生學習數學的信心。）

師：如果要證明平行四邊形四條邊的平方和等于兩條對角線的平方和呢？能不能利用初中學過的幾何法來進行證明？

師：能不能利用坐標法來證明？如果可以的話，如何建系？如何設點？

建系是本節課的難點。為了突破難點，在這里要求小組合作解決，并在討論完后，小組選派代表展示他們的建系方法。讓學生自己對比、分析得出哪些系建的比較恰當，哪些系建的不易得出點的坐標，進而總結出建系的原則與標準。通過展示對比建系的方法，讓走彎路的同學明白自己思維的障礙點，從挫折中磨煉其意志品質，培養其勇于挑戰困難的意志與勇氣。

（二）了解數學史

眾所周知，每個數學概念和公式背后都有著它的故事：或許源于一個靈感;或許是幾代人甚至是幾個世紀人的共同努力使之完善的過程。這種“一次次建立概念、一次次推翻概念、一次次修正概念、一次次完善概念”的艱辛過程，正是教育學生面對困難與挫折，嚴謹認真、頑強拼搏的最好素材。在本節課最后，我還向學生介紹了笛卡爾建立坐標系的一個有趣傳說：

在笛卡爾之前，幾何是幾何，代數是代數，它們各自為政，互不相擾。但是，傳統的幾何過分依賴圖形和形式演繹，而代數又過分受法則和公式的限制，這一切都制約了數學的發展。笛卡爾一直期待著找到一種方法，架起溝通代數與幾何的橋梁。一天，他生病臥床，又想起了這個折磨他很久的問題。天花板上，一只蜘蛛吐絲結網，忙個不停。要結一張網，蜘蛛該走多少路啊！他先把蜘蛛看成一個點，那么這個點離墻角有多遠呢？離墻的兩邊多遠？昏昏沉沉的，他思考著，計算著，不知過了多少時間，笛卡爾突然感覺茅塞頓開：要是知道蜘蛛和兩墻之間的距離關系，不就能確定蜘蛛的位置嗎？確定了位置后，自然就能算出蜘蛛走的距離了。于是，他鄭重地寫下了一個定理：在互相垂直的兩條直線下，一個點可以用到這兩條直線的距離，也就是兩個數來表示，這個點的位置就被確定了。就這樣，笛卡爾建立了直角坐標系。它第一次用數形結合的方式將代數與幾何聯系了起來。

通過學習，讓同學們感受到：笛卡爾的堅忍不拔和鍥而不舍的探索精神，為學生樹立了學習的榜樣。這段史料很好的培養了學生在學習的路上不畏艱難、勇于進取、艱苦奮斗的奉獻精神！

總之，對于數學課堂的德育滲透，有很多的教育契機和切入點。只要善于捕捉好的教育素材，并考慮好學生的思想實際和知識的接受能力，因勢利導，循序點化，就一定能達到“春風化雨潤心田”的效果！

參考文獻

[1]中華人民共和國教育部.普通高中數學課程標準（2017年版2020年修訂）[S].北京：人民教育出版社，2020.

[2]魯基教.山東省中小學德育課程一體化實施指導綱要[S]，2016.

[3]何藝妍.德育教育在數學教學中的滲透[J].中學教學參考，2011（29）.