基于GeoGebra的高中數學課題教學研究
吳國強

摘要:為了能夠有效提升GeoGebra的高中數學課題教學實效性,本文通過具體論述GeoGebra的高中數學課題教學策略,為增強高中學生的數學素養提供可參考的資料。
關鍵詞:GeoGebra;高中數學;課題
GeoGebra界面中包含了諸多的基本元素,如向量、角、函數、直線、點等。當然,也正是基于眾多元素的不同組合與排布,方使得圖像也具備了“動態化”的特征,繼而可將原本枯燥、抽象的內容生成過程以直觀化的形式進行呈現。這將進一步增添圖像的可觀性。不僅如此,GeoGebra中還內置了非常多的屬性,除了最為常用的幾何屬性外,指令區中包含的各類屬性也具備了眾多的功能。諸如計算圓錐的曲線、正多邊形、切線、函數、離散、統計以及列表等。除此之外,GeoGebra上的多元化屬性還能讓圖形呈現出更佳的視覺效果,如針對文本格式的調試、對顏色、位置的掌控以及樣式等。至于GeoGebra作圖則有兩種最為常見的應用方式,分別為“尺規作圖”與“代數輸入”。其中,“尺規作圖”主要運用了繪圖工具中包含的各類作圖基本元素。如多邊形、滑竿、點、直線等。而代數輸入則是利用了函數方程式,通過將函數方程輸入到指令區域內邊疆得到相應的函數圖像。
一、多角度揭示概念內涵,合理進入課堂教學
基于數學概念本身具有的多元、多樣、復雜、抽象等特征,故在揭示其內涵時亦當基于不同的背景、層次以及結構等眾多角度進行。如此方能讓學生對概念產生一個較為完整的認知。諸如針對“函數概念”的相關內容教學,借助GeoGebra則相關函數概念的刻畫則可由解析式、圖像及表格三方面結構切入。
首先,指導學生參與策略。相較于教師的傳輸與交到,學生通過自身的摸索或是直接操作相關模型,勢必更能掌握其中概念。因此,針對概念部分的具體教學,教師需將第一要務放到激發學生學習的主觀能動性之上,以此為學生探索概念本質屬性提供一個良好平臺并進一步提升學生的課堂參與度。
其次,形成概念體系。針對概念的學習并不能將之作為獨立章節,原因便在于眾多概念的形式過程本身便有著極為密切的關聯。
二、優化教學過程,鍛煉學生數學思維
基于GeoGebra的高中數學課題教學時,應該優化教學過程,注重學生的數學思維鍛煉。例如,以橢圓的標準方程這節內容為例進行分析:
對于“橢圓”章節的具體教學,教師的主要教學目標有如下幾方面:一是橢圓的定義;二是坐標系的建立;三是橢圓標準方程。當然,該過程教師可使用GeoGebra來為學生展示相應模型,隨后一步步指引學生去總結橢圓定義。在探索出橢圓定義后,教師同樣可基于GeoGebra來推導橢圓的標準方程。如此一來,學生不僅能學習到相關知識,同時也能強化他們發現與總結規律的能力,繼而逐步形成嚴謹的數學思維。
除了上述教學方法外,教師亦可采取學生合作學習的方式,以此還能同步培養學生的合作交流能力,這對學生今后的學習及發展均有較大助益。
教學難點:推導橢圓標準方程
教學過程:首先,創設情境、導入新課利用 PPT 投影儀展示生活中常見的橢圓形建筑物,并提出問題.如圖2:
問題:PPT上顯示為何種圖形?還有哪些事物與之相似呢?
預設學生活動:橢圓、盤子、籃球投影等。
在學生舉例后,教師又可為學生講述與該知識相關的故事。如針對圓錐曲線的教學,教師便可為學生講述古希臘時代人們運用平面切割圓錐的方式獲得曲線的事例并借助GeoGebra來加以戰士。如此學生勢必能快速找準本章節的學習重點并形成完整的知識體系。
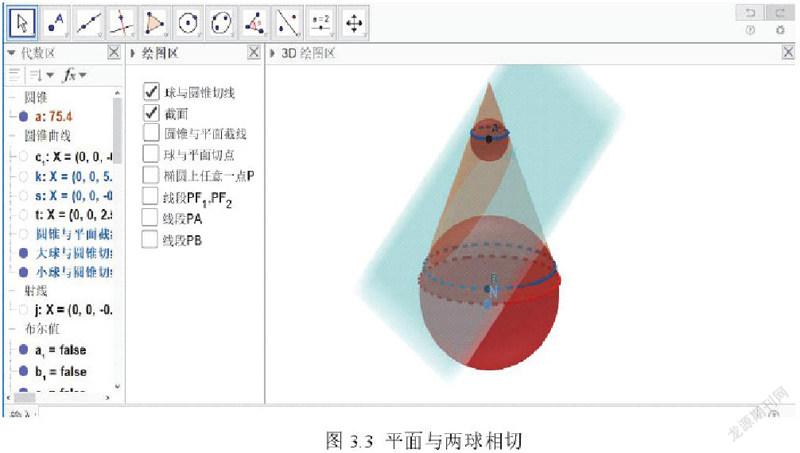
教師向學生展示書上閱讀內容里的數學科學家 Germinal Dandelin 從純幾何的角度證明平面截圓錐是一個橢圓.在圓錐里放置兩個球,一平面與兩球相切,如圖3所示:
讓學生回顧本節課學歷哪些知識點,并強調要注意雙曲線定義的重點以及與橢圓的區別。
就傳統教學而言,針對雙曲線定義部分的具體教學往往僅是基于拉鏈的開合,隨后的雙曲線定義、焦點、焦距等內容同樣基于此。這不僅讓教學過程顯得過于簡易且并不能讓學生體會知識的形成過程,繼而也很難對學生思維產生有效培養。因此,為規避以上教學避免。教師可充分利用GeoGebra來為學生詳盡呈現雙曲線相關知識的形成過程,如此一來,學生在建構知識輪廓時勢必更為完整,繼而也能深化學生對知識的記憶與理解。
總之,將GeoGebra引進高中數學教學不僅能幫助學生更好地理解數學知識、概念、定義等極具抽象性的內容,同時還能有效激發學生的學習興趣。因此,教師亦當對GeoGebra的引進給予高度重視,繼而在保證良好的教學效率同時亦為學生今后的學習及發展奠定牢固基礎。
參考文獻:
[1]張志勇. GeoGebra軟件在高中數學教學中的應用舉例[J].福建中學數學,2014(4):6-9.
[2]寇恒清. GeoGebra在高中數學教學中的應用初探[J].數學通報,2015(9):48-51.

