巧用轉化，玩轉數學

張彩萍

【摘? 要】轉化思想是數學核心思想之一，它在蘇教版教材中有所體現，也是解決問題的主要策略之一。不難發現，在日常教學中，很多教師對此思想的應用完全不夠，致使部分內容的教學效果大打折扣。因此，在教學中，教師應巧用轉化思想，善于引導，將轉化思想應用于數學教學之中。

【關鍵詞】轉化思想;小學數學;數學教學;蘇教版

蘇教版小學數學教材將轉化作為解決問題的策略單獨教學并著重強調。熟知教材便不難發現，轉化思想并不存在于一個課時或一節數學課中，它已然貫穿整個小學數學教材，深入幾乎每一課中。因此，了解轉化思想的應用，并將之滲透于日常教學尤為重要。

一、知其用途，理解轉化

（一）由繁入簡，優化策略

在解決一些小學數學問題時不難發現，對于一些復雜問題，如果直接去處理、解決，難以找到著手點。此時可借助轉化的思想方法，分析問題后，將復雜的問題簡化，以尋找新的簡單的生長點和著力點。

轉化思想在蘇教版教材中的體現：在蘇教版小學數學四年級下冊的學習中，將復雜的綜合算式通過運算律簡化，轉化成便于計算的簡單算式;在六年級上冊，在計算不規則物體體積時，將物體放入有刻度的水量杯中，將物體體積轉化為可測的水的體積，將問題簡化等。

不規則圖形面積的求解是蘇教版五年級下冊學習的一個重難點，因為圖形的不規則性，所以學生很難或無法直接求解。

如蘇教版五年級下冊《解決問題策略——轉化》中的例1：下面兩個圖形，哪個面積大一些？

學生以前比較面積大小的方式一般為觀察法、重疊法，最準確的就是計算法。顯然，在這個問題中，觀察法和重疊法都無法使用，所以要用計算法。但是計算不規則圖形面積，直接計算，于五年級生而言比較困難，計算煩瑣，學生有些犯難。

因此，教師可引導學生將復雜的不規則圖形轉化為簡單的常見幾何圖形：

通過轉化，可將上圖中不規則的圖形轉化為規則的長方形。

1.可以直接看出兩幅圖面積相等。

2.可以利用長方形面積公式——S=ab，直接求解。

通過轉化，能將復雜的、難以直接解決的問題轉化為簡單的問題，輕松解決，優化解決問題的方法。

（二）以舊衍新，遷移新知

以舊衍新，即通過轉化，將以前未接觸未學習過的新知識轉化學生已經接觸并掌握的知識進行學習，將遇到的新問題轉化成學生已經熟悉的問題去解決。通過原有知識和新知識之間的聯系，實現轉化，使知識獲取更簡單。

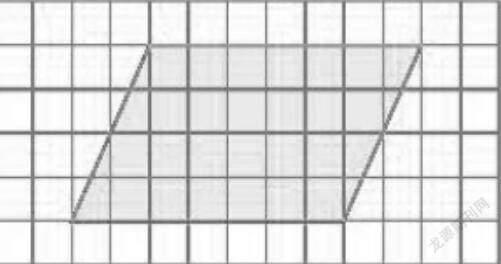
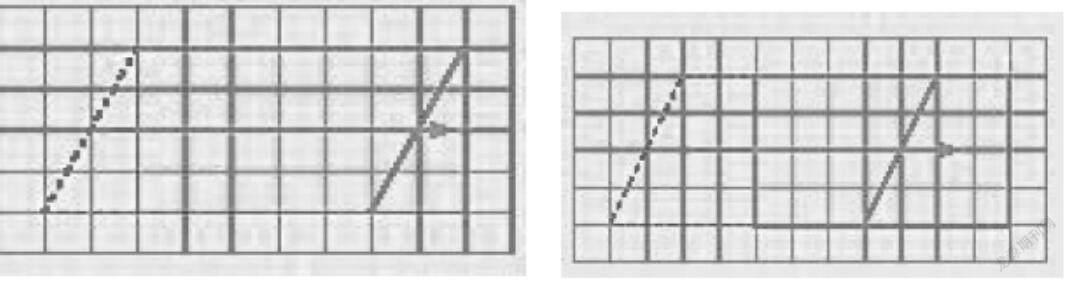
在小學數學教學中，通過轉化以舊衍新，無處不在。在計算中，將小數的計算轉化為學生熟悉的整數計算，遷移計算方法;將異分母分數轉化成同分母的分數進行相加減，這樣能極大地降低計算難度;將分數的除法轉化為分數的乘法進行計算;在幾何圖形的計算中，將平行四邊形通過剪切、平移等方式，轉化成和它面積相同的長方形進行計算;將三角形和梯形的面積通過拼接等方式，轉化成平行四邊形進行計算等。如蘇教版五年級上冊《平行四邊形的面積》一課中的例1：你能將下面平行四邊形轉化成長方形嗎？

教材出題者沒有讓學生直接計算平行四邊形的面積，而是將之先轉化為學生已知的長方形，再進行下一步研究。學生得出兩種轉化的方式（如下圖）：

緊接著，教材出示“將書本115頁的長方體剪下來，剪一剪，拼成長方體填表”。通過教師的引導，學生能夠得出：

1.平行四邊形的底通過轉化成為長方形的長。

2.平行四邊形的高通過轉化成為長方形的寬。

3.平行四邊形的面積通過轉化成為長方形的面積。

平行四邊形面積=底×高

長方形的面積=長×寬

通過轉換，進行知識遷移，學生能夠很快得出平行四邊形面積的計算公式。

通過轉化，將新知與舊知聯系在一起，學生能夠快速獲取新知識。

（三）化曲為直，突破障礙

在小學數學學習階段，化曲為直主要應用于曲面的求解。更直接地說，化曲為直應用于小學階段圓的學習——求解圓的周長與面積。

在數學學習中，曲線或者曲面太難直接測量，或者說不可直接測量，這時轉化思想尤為重要。

如蘇教版五年級下冊第二單元《圓的周長》例5：幾人一組，用硬紙板剪出3個大小不同的圓，想辦法量出它們的周長，再計算出周長除以直徑的商，并把表格填寫完整。

（四）寄數于形，提升思維

寄數于形，將數轉化為形去解決問題是教學蘇教版小學數學教材時常用的一種方法。對于大部分小學生來說，對于條件較多、數據之間聯系復雜的問題，他們不太能夠通過直接讀題來分析問題，明確數量之間的關系，學生在解決問題時常常無從下手。此時，就需要將較復雜的數據類問題，通過轉化形成圖形問題，從而借助圖形的直觀，看清數之間的聯系，理清數量關系，以解決問題。

蘇教版教材中對以數化形的問題安排較多，主要體現在小學中、高年級解決問題的策略中。和差問題與差倍問題是蘇教版四年級下冊學習的一個重難點，此類問題只有數據支撐，學生通常無從下手。

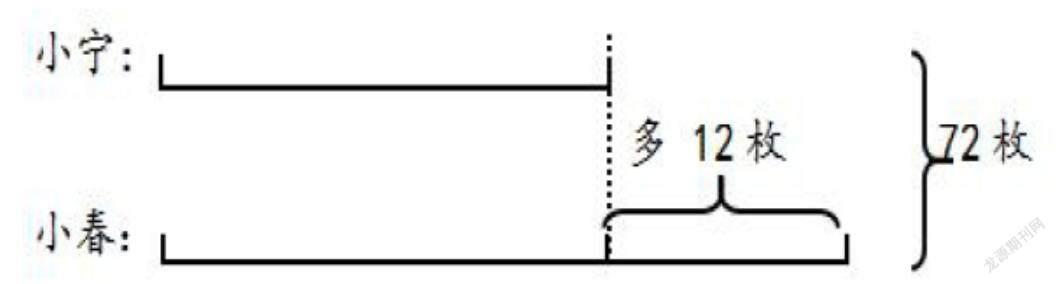
如蘇教版四年級下冊《解決問題策略——畫線段圖》例1：

“小寧和小春共有72枚郵票，小春比小寧多12枚。兩人各有郵票多少枚？”

在之前的學習中，一般告訴學生一個量以及所求量與這個量的關系，求取所求量。而在此類問題中，只告訴兩個量之間的兩個關系，求取這兩個量，學生開始犯難。但是如果將數轉化到線段圖中，就簡單多了。

線段圖如下：

從上圖中可輕易看出小寧與小春郵票數之間的關系，而解題的關鍵是通過將線段的“割” “補” “分”使兩條線段長度一樣。

以“補法”為例：通過將短的線段補齊，讓小寧與小春郵票數量相等。求出小寧如果與小春郵票數相等時，共有票數為72+12=84（枚），將總郵票數平均分成兩份求出小春郵票數。小寧的郵票數就求出來了。

小學數學中有些問題數量關系比較復雜，小學生解題無從下手，將問題條件寄予圖形，便于分析，從而降低問題難度，便于解決問題。

二、巧用方法，滲透轉化

（一）善用類比，逐步轉化

類比法是將新舊內容進行比較，找出其相似點，然后根據它們之間的相似點用已知的知識推理出未知的對象。這種方法不僅有利于學生對新知的學習，更有利于學生對舊知的鞏固。例如，教學“三角形的面積”時，筆者引導學生通過剪、拼等方式，將三角形轉化成長方形，三角形的底一般是長方形的長，高轉化為長方形的寬。通過轉換，學生可自主進行三角形面積計算公式的推導。

蘇教版小學數學教材的編排中處處滲透著轉化思想，它們都是將沒有學過的知識通過類比的方式轉化成學生已有的經驗或知識儲備，符合學生的認知，有利于學生數學邏輯的發展。在教學中，教師應密切關注新舊知識之間的聯系，在轉化中讓學生感受到數學知識的整體性。

（二）聯想遷移，滲透轉化

解決數學問題需要學生具有一定的聯想與遷移能力。教師在教學中可通過聯想與遷移，不斷滲透轉化思想方法，從而豐富學生的學習經驗，提升學生的思維能力。

例如，教學蘇教版六年級下冊找規律課“面積的比”時，在學生探究完圖形的長度比與面積比之后，接下來作為拓展，教師可引導學生思考：若兩個正方體的棱長比是1∶2，它們的體積比是多少？學生通過回憶探究面積之比的過程，自然而然會聯想到體積比是1∶8。從線到面的過程，可用畫圖的方式進行操作。從面到體的過程，更多就是通過聯想，實現一個從一維圖形到二維圖形再到三維圖形的維度遷移，學生最終可通過長度比和面積比推導出體積比。

通過聯想遷移，將新的問題轉化成已經學習和探索過的知識進行推導，不僅可以簡化學生獲得新知的過程，還可以提升學生思維能力，從而提高他們解決問題的能力，特別是對將來學習和立體圖形相關的知識有極大的幫助。

（三）擅于假設，實現轉化

近年來，課標對學生分析問題、解決問題的能力有進一步的要求，解決問題也成為數學教材中的重要組成部分。在小學階段，學習解決問題的過程中，教師引導學生將問題向已有條件轉化，有助于學生更直接、更有效地理清思路。其中引導學生進行假設和替換就是非常有效的方法。如六年級學習的雞兔同籠問題，學生通過假設籠子里全是雞或者全是兔子，通過腿產生的差量去求解，就能將未知的問題轉化為已知條件——雞和兔子的只數。通過假設，實現轉化，將問題簡化。

作為數學學習中的重要思想，轉化對提升學生的數學思維能力起著巨大的作用。根據教材的編排以及學生已有的認知結構，教師在日常教學中要積極鉆研，讀懂教學中蘊含的轉化思想。同時，教師應當了解小學數學各知識之間的聯系，引導學生進行聯想，并利用轉化的思想舉一反三，獲得知識的拓展和思維的提升。教師在教學中不斷滲透轉化的思想，能使教與學達到事半功倍的效果。

【參考文獻】

[1]黃麗琳.激發小學生數學應用題學習興趣的有效研究[J].兒童大世界：教學研究，2017（01）：145.

[2]全云.小學數學應用題教學中存在的問題及優化策略探究[J].中國校外教育，2018（10）：127-130.

[3]韓志忠.小學高年級數學應用題解答能力的培養策略[J].課程教育研究，2019（38）：155-156.

[4]中華人民共和國教育部.義務教育數學課程標準（2011年版）[S].北京：北京師范大學出版社，2012.