小學“數與代數”領域幾何直觀能力培養現狀調查

楊玉才 孫曼曼

摘要：本文探究了小學數學“數與代數”領域幾何直觀能力培養的現狀，提出了相應對策，為促使教師在具體的教學過程中能根據“數與代數”領域的教學內容，自覺培養學生的幾何直觀的意識和能力做貢獻。

關鍵詞：幾何直觀 ?小學數學 ?學情 ?數與代數

一、調查背景

（一）《義務教育數學課程標準（2011版）》中的要求

《義務教育數學課程標準（2011版）》中指出幾何直觀在數學學習過程中的發揮著重要作用。借助幾何直觀可以把復雜的數學問題變得簡明、形象，有助于探索解決問題的思路，預測結果。同時在第二學段的“數學思考”目標中明確提出了讓學生“感受符號和幾何直觀的作用”的要求。因此，在小學數學“數與代數”領域培養小學生幾何直觀能力是十分必要的。

（二）小學“數與代數”領域關于幾何直觀的研究現狀

目前，國內有不少關于幾何直觀能力的發展研究，且成果顯著。縱觀同類課題和研究的案例，大多數都是對幾何直觀的數學思想方法作大量文字性敘述說明，偏向研究應用。在小學數學“數與代數”領域怎樣利用幾何直觀具體化、形象化的特性，把數的概念建立、計算的算理算法、解決問題的思路和方法具體化、形象化，發揮幾何直觀的教學價值，并未有具體的策略。

二、研究小學數學“數與代數”領域幾何直觀能力培養的意義

兒童以具體形象思維為主，處于第一學段的兒童尤為突出。高年級學生的抽象邏輯思維雖有了一定的發展，但仍以形象思維為主，理解一些數學概念、計算算理及解決問題時仍離不開形象思維。借助具體的實物、幾何圖形或示意圖呈現題意，把抽象的文字直觀化，給學生搭建思考問題的支點，學生易于找到思維的突破口，進而找到解決問題的思路和方法。同時，幾何直觀也有助于發展學生的直覺思維，有利于學生猜想和驗證。教學中我們發現，學生有越強的幾何直觀能力，對抽象數學知識的理解就越容易、越深刻，學習效果就越好，有時可以達到事半功倍的效果。

三、調查對象與方式

為使本次調查研究更具有普遍性和針對性，針對小學“數與代數”領域幾何直觀的培養策略的研究現狀，我們對北附小聯盟和城鄉第三教育集團學校師生開展了一次問卷調查，調查的學校涵蓋縣城小學和鄉鎮中心小學、村小，共發出500份調查問卷，收回484份有效問卷。

四、調查情況及其分析

（一）教師的“教”情

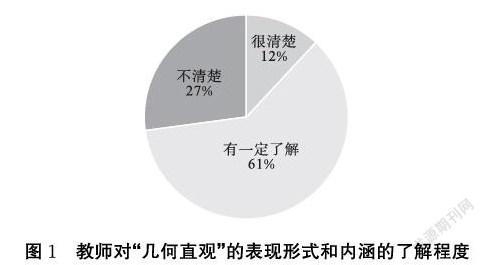
調查結果顯示，教師對幾何直觀的呈現形式和內涵了解程度很清楚的只占12%，有一定了解的占61%，不清楚的占27%;除了教材中已有的素材，經常從其他途徑獲得幾何直觀材料的只占18%;在“數與代數”領域的教學中經常自覺用幾何直觀幫助學生理解數學概念、運用數學知識解決問題的教師占16%，偶爾運用的教師占79%，從不用的教師占5%。

但是97%的小學數學教師都認為對學生的幾何直觀能力的培養和發展的關鍵期是小學階段。該階段在促進學生對數學實際內涵的理解方面起著不可替代的作用，能積極促進學生直觀思維的發展。98%的小學數學教師認為在“數與代數”領域培養小學生的幾何直觀能力有必要具備相應的教學策略。

（二）學生的“學”情

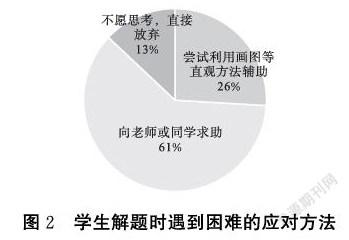
調查結果顯示，學生遇到問題時，能自覺運用幾何直觀輔助思考的占26%;向老師或其他同學尋求幫助的占61%;一點都不愿意思考，就直接不做的占13%。但大約98%的學生都認為圖形可以表示數學信息并對他們學習數學有幫助，特別是學習抽象的數學概念、計算算理、較復雜的問題時，借助圖形直觀形象化的特性，可以變隱形為顯性，變抽象為直觀，變復雜為簡單，便于加深對知識的理解，尋找解決問題的思路和方法，進而正確地解決問題。

（三）調查分析結果

很大一部分教師，對幾何直觀的概念理解不透，認為幾何直觀專屬“圖形與幾何”領域，很少在“數與代數”領域去研究學生幾何直觀能力的培養策略。

小學數學教師在“數與代數”領域的教學實踐中對幾何直觀認識不足，忽視數和形的互補作用，在講解數學概念時教學方法比較單一，學生理解得模糊不清。

教師對教材的設計意圖把握不到位，在教學中很少研究如何培養學生的幾何直觀能力。教材比較重視對學生幾何直觀的培養，但只是靜態地呈現。例如，在教材中，圖形都是直接呈現給學生，具體該怎樣畫圖卻沒有詳細完整地體現出來。如果沒有把畫法動態化地呈現給學生，不利于學生在遇到問題時自覺運用幾何直觀能力輔助解決問題，特別是低年級學生。

很多學生在解決問題時不能自主地借助幾何直觀來尋找解決問題的思路和方法，缺少變通能力，不能靈活、快捷、正確地解決問題。他們在解題時只是偏向于套用公式，不能“賦數于形”，缺乏使用幾何直觀解決問題的意識。

上述中的問題說明了小學數學教師形成幾何直觀意識、優化幾何直觀教學策略的必要性。只有形成了一定的幾何直觀教學策略，才能有計劃、有步驟地落實小學階段的幾何直觀培養目標。

五、在小學數學“數與代數”領域培養學生幾何直觀能力的策略

1.組織數學教師學習幾何直觀的相關理論，提高其認識。

2.轉變數學教師的教學思想，使其深刻認識到幾何直觀對發展學生數學思維方面的重要意義，增強教師在教學實踐中對學生幾何直觀能力培養的意識。教學中有計劃、有目的地對學生進行有階段性的、循序漸進的引導，使學生形成借助幾何直觀尋找解決問題的思路和方法的良好習慣，從而正確地解決問題。

3.解讀教材、交流梳理知識體系，分析整理幾何直觀在“數與代數”領域各年級教材中的體現，便于有針對性地滲透幾何直觀。

4.進行培養小學生幾何直觀能力的典型案例研究，培養小學生運用幾何直觀的方法。

參考文獻：

中華人民共和國教育部.義務教育數學課程標準（2011年版）[M].北京：北京師范大學出版社，2012.