數形結合思想在高中數學解題中有效滲透的思考與實踐

皇甫海峰

摘要：相對其他高中學科來說，數學這一學科的知識內容更加抽象，使得許多學生在學習過程中容易感到困難，甚至一部分學生常常會因為細節上的失誤而走入困境。對此，高中數學教師有必要創新教學方式，一方面降低學生對數學知識的認識和理解難度，另一方面鍛煉和提高學生的理解能力、解題能力等，致力于從各個方面克服數學教學與數學學習的困難，促進廣大高中生在數學方面全面提高、全面進步。本文以數形結合思想的概念闡述開篇，講述了高中數學解題教學的困境，也結合了實踐教學探討了數形結合思想在高中數學解題教學中的應用策略。

關鍵詞：數形結合;高中數學;本質教學;知識銜接

受傳統教育觀念的影響，許多高中教師常常會陷入同一種教學思路中，難免千篇一律。雖然這些教學思路不是錯誤的，但在現代教育中一定存在局限性，這對于數學解題教學的長效發展是不利的，同樣不利于學生的數學綜合水平提升。也就是說，高中數學教師不能局限在同一種思路里教學，應當結合特定的數學知識巧用教學方法、結合學生的不同素質巧用教學技巧。如在數學解題教學過程中，教師就可以融入數形結合的思想，讓學生學習并掌握這樣的解題技巧，強化每一位學生舉一反三、學以致用的能力。

一、數形結合思想的概念闡述

數學概念由數字思維和圖形思維共同組成，而且“數”與“形”之間也可以相互轉化。數形結合思想也就是利用“數”與“形”的轉化關系解決實際問題，將未知量轉化為已知條件，為解決問題提供先決條件。對于高中數學教師來說，我們的任務就是熟練掌握這一解題技巧的運用，同時圍繞其核心、要點講給學生聽，讓學生也能夠將其融會貫通和應用到解決問題中。解題教學過程中，數學教師首先要做的是舉例論證，也就是找出一道題目的重點，將其中抽象、難懂的部分轉化為圖形展示給學生看，而后結合圖形列出方程、算式，便于學生理解這一抽象的過程，幫助學生找到解決問題的方法。

二、高中數學解題教學的困境

（一）高中生的解題思維較為淺顯

現階段，高中數學教師對數形結合思想的運用還不夠成熟，以致學生面對難題時也只能就題論題，無法達到舉一反三、學以致用的教育效果。也就是說，教師的思維局限對學生的影響很大，許多高中生學習方式死板、學生思維固化也正是這一原因導致的。當然，其中也不排除學生個人數學基礎不扎實、學習態度不端正等等因素。由此可見，數形結合思想在高中數學教學中的融入不是一蹴而就的，這取決于師生雙方的動力和努力共同作用。數學教師應當多運用這一方法示例，而學生也要透過現象看本質，早日熟練掌握此類學習方法。

（二）高中生之間的思維具有差異

高中生之間存在巨大思維差異，每一位學生都有著獨特的思考方式，而他們運用的解題方法也各不相同。這也正是一部分學生學不好數學的主要原因，也就是他們所應用的解題方式完全走進了誤區。對此，高中數學教師有必要結合數形結合的思想開解學生，降低學生理解數學知識、題型的難度，讓學生找到解決數學實際問題的切入點去解題、去發現和探索。此外，數學教師還有必要結合不同學生的特點對癥下藥，采取分層教學、分層作業的方式輔導學生，讓學生在解決數學問題時抱有更多耐心與細心。久而久之，高中生也能夠養成良好的做題態度、做題習慣，進而能夠通過反復練習真正掌握數形結合的解題方法。

（三）高中生缺乏對知識點的歸納總結

現代教育改革對高中數學提出了更高的要求，在運用基本方法和基本技能的同時，如何快速地把做題時遇到的問題同其他知識點的聯系起來提出了更高的要求。這對學生的發散思維提出了更高的要求，打通知識點的聯系樞紐至關重要。例如在求解三角函數周期問題時，如果我們在回歸基本函數的同時，結合基本函數周期性的特點，畫出該函數的草圖對解決問題起到至關重要的作用，也能降低問題的復雜程度，從而提高中學生學習數學的熱情。

三、數形結合思想在高中數學解題教學中的滲透策略

（一）抓住數形結合的核心思想進行示范教學

數形結合思想在高中數學解題教學中的滲透可以通過示范教學實現，也就是教師需要從復雜的概念、定理、公式等中提煉出數學思想，通過示范讓學生理解其核心意義，讓學生利用核心意義解決數學題目。這是一個由教師引導產生的過程，還需要以教師為媒介構建數學知識與學習者之間的關系，幫助學習者掌握題型和解題方法的奧秘。

例如，在講解“橢圓”這一部分知識內容時，高中數學教師可以先按照一般步驟教學，帶領學生經歷橢圓的形成過程，讓學生理解橢圓的定義，明確焦點、焦距的概念，并類比圓的方程推導出橢圓標準方程。這一過程中，數學教師還可以融入情境教學、師生互動等具體環節，幫助學生理解橢圓的標準方程得出過程。接著，數學教師就可以引入示例教學，結合數形結合思想解決圓錐曲線的相關問題。

【題目】

【分析】

當然，老師也可以結合圖形進行直觀分析，線段|AB|的長即為橢圓的路徑，運用公式直接求出短軸長，從而求出橢圓的標準方程。無論是方法一還是方法二，目標是讓學生對橢圓的圖像和性質有進一步的了解，讓圖形在學生腦海中生根，公式性質等數據信息發芽。

2.做好知識銜接進行串聯式教學

數學教師除了要教會學生應用解題方法外，還應當強調知識之間的關系，讓學生串聯數學知識、聯想數學知識，培養學生良好的數學思維。對于數學知識來說，不同章節的知識點串聯有助于學生理性思考，同一章節的知識點串聯能夠幫助學生解決實際問題。也就是說，數學教師有必要做好知識銜接，通過這一方式鍛煉和提高學生的解決問題能力。

例如，在講解“拋物線”這一部分內容時，高中數學教師就可以總結出單元教學模塊，將本單元知識內容分為拋物線的幾何情境、拋物線的幾何特征與概念、拋物線的標準方程、拋物線的簡單幾何性質。雖然本單元知識可以進行模塊劃分再教學，但后三者間有著密切聯系，其聯動與融合能夠解決拋物線相關的實際問題，同樣能夠達到有效、高效的教學效果。

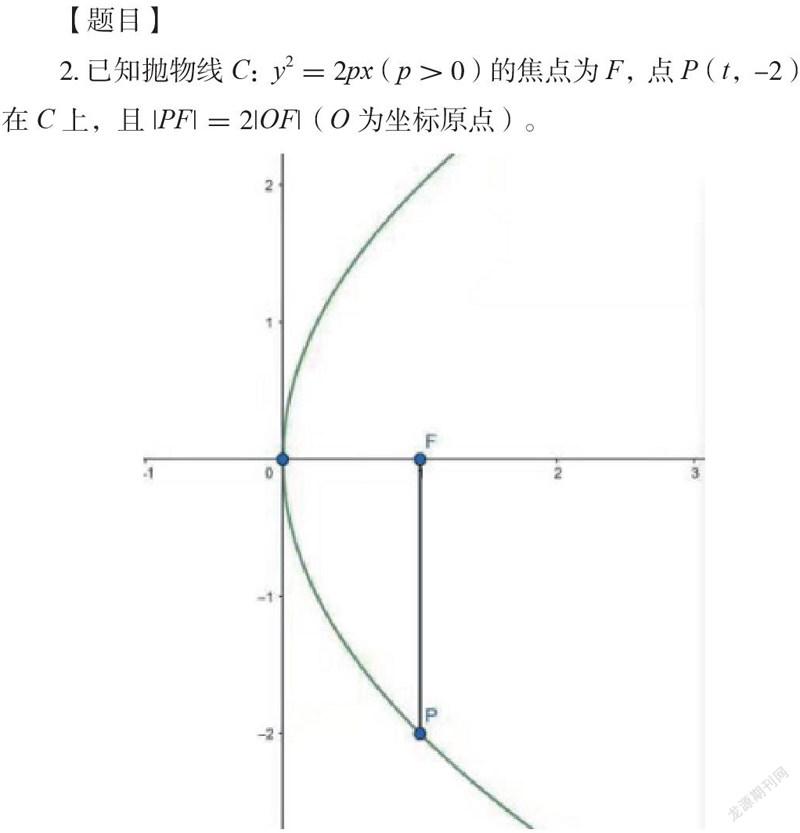
【題目】

2.已知拋物線C：y2=2px（p>0）的焦點為F，點P（t，-2）在C上，且|PF|=2|OF|（O為坐標原點）。

（1）求C的方程;

（2）若A，B是C上的兩個動點，且A，B兩點的橫坐標之和為8，求當|AB|取最大值時，求出直線AB的方程。

【分析】

（1）利用已知條件，列出方程組，求解p，即可求出C的標準方程。

（2）設A（x1，y1），B（x2，y2），且x1+x2=8.設AB中點為D（m，n），當x1=x2時，lAB：x=4，|AB|=8;當x1≠x2時，求出直線的斜率，直線方程，然后直線方程與C聯立方程消去x，整理得y2-2ny+2n2-16=0，利用韋達定理，弦長公式求解即可。

求解第一小題時應先做出拋物線的圖像，再運用拋物線的定義列出方程，從而求出拋物線的方程。在教學中不僅培養提升了學生的直觀想象能力，也培養了學生的辯證思維能力。將傾斜長度轉化為水平距離，使問題的難度系數得以下降。

教學過程中，教師應借助幾何畫板或GGB等網絡技術，畫出拋物線的圖像，結合已知條件確定，未知量通過假設，由題目給出的條件與拋物線的性質求出橢圓標準方程。通過示例，學生能夠掌握。

求解第二小題應用數形結合代入點求解直線斜率、直線方程。這一過程需要諸多拋物線的基礎知識聯動求未知量，也就需要學生掌握本單元知識間的聯系。基于此，教師有必要串講單元知識內容，并附上示例講解，讓學生在掌握所有基礎知識的同時對比圖形與已知條件，得出線段|AB|長度表達式，進而運用基本不等式求解。后續通過變式訓練、反復應用，提高學生的解決問題能力。

三、結語

總而言之，數形結合思想在高中數學解題教學中的融入不是一蹴而就的，也不是剛剛結合使用就能夠收到良好效果的。高中數學應當抱著量變積累質變的想法不斷嘗試、不斷創新，爭取通過數形結合幫助學生找到恰當解題思路，發散學生的解題思維，鍛煉和提高學生的創新能力。久而久之，高中生的數學解題能力、解題水平也將會自然提升。

參考文獻：

[1]任明耀，劉芬.改進高中數學解題教學的嘗試——錯題資源的建立與利用[J].科學咨詢（教育科研），2018（08）：86-87.

[2]李曉明.高中數學教學與解題中數形結合思想方法的應用分析[J].中國新通信，2018，20（07）：209.

[3]張藝璇.關于高中數學幾何解題技巧之“數”“形”結合策略[J].亞太教育，2015（34）：73.