培養幾何直觀能力 發展數學核心素養
俞丹鋒
摘要:數學是一門研究空間形式與數量關系的基礎學科,是脫離具體事物的抽象化的知識。在數學教學中培養學生幾何直觀能力,能幫助學生將抽象的邏輯較強的數學問題利用圖形直觀化、具體化、簡單化。教師在數學教學中要轉變教學觀念,注重學生直觀感知,積極滲透數形結合思想,強化學生畫圖技能,加強實踐操作,運用現代化教學技術,培養學生的幾何直觀能力,發展學生的數學核心素養。
關鍵詞:數學教學;幾何直觀;核心素養;能力培養
中圖分類號:G421;G623.5文獻標志碼:A文章編號:1008-3561(2022)14-0067-03
到了小學中高年級,學生的數學學習常常出現較為突出的兩極分化現象,究其原因,是數學知識的抽象程度隨學段的提高而加深。對不同年級數學教材進行對比,可以發現低年級的教材中例題和練習配套的直觀圖形較多,中年級教材中配套的圖形明顯減少,高年級知識以及練習呈現主要以文字說明為主。面對純文字、沒有配套直觀圖形的練習,學生感到理解題意比較困難。因此,在小學中高年級培養學生幾何直觀能力的重要性就凸顯出來。在小學階段培養學生的幾何直觀能力,教師可以從以下幾個方面著手。
一、轉變教師教學觀念,重視幾何直觀能力培養
《義務教育數學課程標準(2011年版)》提出幾何直觀以后,很多教師認為培養學生的幾何直觀能力非常有必要,但在教學中卻常常出現一些問題,主要表現在以下幾個方面。首先,教師對“幾何直觀”的理解不夠全面,認為幾何直觀能力只能在與幾何相關的題型的教學中才能進行培養,這是一種片面的認識。實際上,在“數與代數”“統計與概率”“綜合與實踐”這幾個知識領域都涉及幾何直觀。其次,部分教師在教學過程中重知識講解,輕能力培養,導致學生的幾何直觀能力培養不足。部分教師為了學生成績的提高對學生進行了大量練習以提高學生對知識點的運用能力,這樣的教學導致學生只能就題論題,舉一反三的能力相對薄弱。
例如,在教學乘法分配律a×(b+c)=ab+ac時,部分教師讓學生記憶公式或者利用諸如“我愛爸爸和媽媽等于我愛爸爸和我愛媽媽”之類的口訣方便學生記憶,這就是只重知識講解的教學方式。學生只會套用,當題目變化后就不會靈活的應用,原因在于沒有理解乘法分配律的內涵。對于四年級的學生來說,理解乘法分配律a×(b+c)=ab+ac這樣抽象的知識點有一定困難。因此,教師在教學例題4×25+2×25=(4+2)×25的時候,除了從乘法的意義方面進行講解,還可以把乘法分配律轉化為圖形的面積幫助學生理解(見圖1)。教師可以引導學生把例題看成求長相同、寬不同的兩個長方形的面積和。直觀的圖形可以給學生留下深刻的印象,使學生明白乘法分配律可以借助長方形的面積來理解,加深對乘法分配律的理解。
教師要改變傳統的教學觀念,以培養能力為導向,準確定位自身在課堂上角色,成為學生學習的“引路人”,給學生大膽發言的機會,讓學生充分討論,在學生遇到困難時適時指點,逐步提高學生解決問題的能力。
二、注重學生直觀感知,讓學生親歷幾何直觀過程
在小學階段,學生的數學思維以形象思維為主,并逐步向抽象思維過渡。在這個階段,教師要根據學生的認知規律,讓學生多角度感知,逐步發展學生的幾何直觀能力。只有讓學生多經歷、多感知,才能將抽象的問題直觀化。例如,“排隊問題”對學生來說就非常抽象。對于“小明的前面有4個小朋友在排隊拍照,他的后面有3個小朋友,一共有幾個小朋友在排隊”這個問題,教師可以先讓學生現場模擬排隊,形成直觀感性的認識,知道共有8人排隊。然后,教師可以在黑板上畫出“○○○○▲○○○”這樣的圖形,引導學生說說圖形的意思。學生根據剛才的排隊活動,能輕松地理解4+3+1=8,并真正理解“1”的由來,明白可以用畫示意圖的方法解決類似問題。通過現場排隊、畫示意圖等方法,學生在直觀感知中經歷了“文字→實物→圖像→總結”這樣的學習過程,將抽象的數學問題變為直觀的圖像問題,提高了幾何直觀能力。
三、滲透數形結合思想,提升學生幾何直觀意識
圖形是抽象數學問題與直觀認識之間聯系的橋梁,在解決抽象的問題中發揮至關重要的作用。數形結合能把抽象的數量關系與圖形有機地聯系在一起,提供解決問題的思路。例如,在豎式計算的教學中,教師可運用數形結合幫助學生理解算理。如對于“16×3”,教師可以借助擺小棒的方法教學,16可以看成10根小棒(即一捆)和6根小棒,16×3是10根小棒和6根小棒加在一起的3倍,或者先計算單根的部分6×3=18(根),滿10根變成1捆還有8根,再算10的3倍就是30即3捆,加上1捆和8根,合起來即48根。結合直觀的實物或者圖形可以讓學生更好地理解算理,明確6×3為什么要向十位進1,降低學生的理解難度。
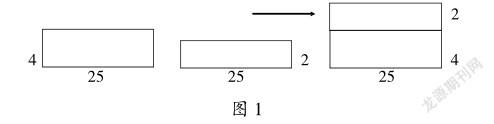
數學學習過程中,一些學生容易受到片面的直觀認識的影響,陷入先入為主的錯誤中不能自拔,而數形結合能讓學生更容易走出認識誤區。例題:三年段組織學生參加隊列比賽,每排有8人,共5排,現因隊形變換需要,要增加3排,且每排增加2人,共需要增加學生多少人?一些學生認為增加了2×3=6(人)。如果教師不借助圖形配合講解,就無法講清題中增加的人數到底在哪個部分,學生理解起來就非常吃力,而利用圖形就十分容易糾正這種認識上的錯誤。學生從圖2中就能直觀地看到白色的圓圈表示的是原來的人數,需要增加的人數就是黑色部分,即(8+2)×(5+3)-8×5=40(人)。學生可以很容易看出來2×3僅是增加的一部分,從而突破理解障礙。