巧用數學題組練習 實現思維能力升級

于昕

摘要：題組練習是數學教學中的一種有效形式，是學生數學思維品質養成的切入點。教師要設計“定點”題組練習，讓數學思維由表及里；要設計“串鏈”題組練習，讓數學思維由淺入深；要設計“構面”題組練習，讓數學思維由窄變寬；要設計“梳理”題組練習，讓數學應用由點到面。

關鍵詞：數學教學；題組練習；數學思維

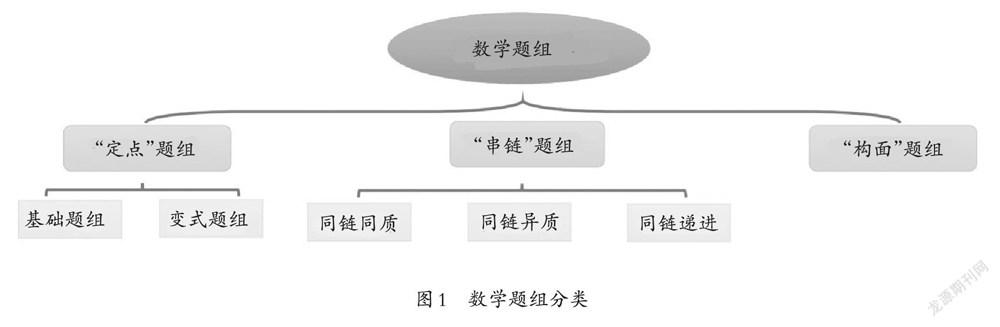
題組練習是數學教學中的一種有效形式，是學生數學思維品質養成的切入點，是通過對照練習，達到對比分析、交流評價、自主創新的層次，打破記憶、理解、應用知識的層面，實現深度學習，促進低階思維向高階思維的轉變。筆者根據教學實踐的經驗總結，從“定點—串鏈—構面”三個方面來設置題組，并將相應題組進行詳細分類，如圖1所示。

一、“定點”題組練習，讓數學思維由表及里

所謂“定點”題組，就是將考查相同知識點的題目編成一組，這一相同的知識點就是“定點”。

以題組一為例，解決這三個問題都需要學生從認知結構已有的圖式中提取圓的面積公式，根據圓的半徑求面積就是這組題的“定點”。這三道題的不同點是第二題需要根據直徑求出半徑，第三題是已知周長求半徑，再運用公式求面積。通過這組題的練習，學生明晰：已知圓的半徑、直徑、周長，求面積。不同題型之間的區別和聯系：求圓的面積需已知圓的半徑，并將這一“定點”存入認知結構中。

【題組一】基礎題組

1.已知圓的半徑，求圓的面積。

2.已知圓的直徑，求圓的面積。

3.已知圓的周長，求圓的面積。

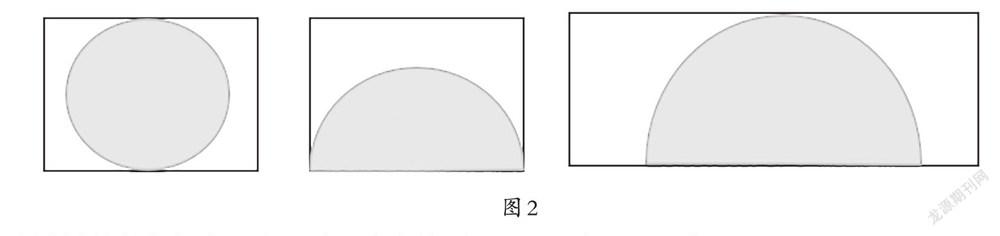
題組一屬于“定點”題組中的基礎題組，實現的是思維“點”狀提升，而利用已知圓的半徑求面積，這一“定點”解決的問題還有很多，教師還可以呈現變式題組（如題組二），這些都是在求圓的面積。但是，不同點是第一題在長方形中切割最大的圓，求此圓的面積，關鍵在于找準圓的半徑即長方形寬的一半；第二題在長方形中切割最大的半圓，求此半圓的面積，關鍵在于知道圓的半徑是長的一半；第三題也是在長方形中切割最大的半圓，求此半圓的面積，區別在于要知道圓的半徑就是長方形的寬（如圖2）。解決此三題雖然運用的“定點”一樣，但是要求圓的半徑需要學生花費一番精力，這樣可以使學生的學習逐步走向深入，實現思維“鏈”上的串通。

【題組二】變式題組

1.一個長方形，長12厘米，寬10厘米，要切割出一個最大的圓，圓的面積是多少平方厘米？

2.一個長方形，長12厘米，寬10厘米，要切割出一個最大的半圓，半圓的面積是多少平方厘米？

3.一個長方形，長24厘米，寬10厘米，要切割出一個最大的半圓，半圓的面積是多少平方厘米？

教師在講授數學內容時，要把握這一內容的“定點”，巧用題組練習，讓練習不僅停留在鞏固新知識的層面上，更要啟發學生去追溯知識的本質和內核。教師要通過題目使學生掌握一組題目的解決方法，理解其中蘊含的數學思想，促進學生的數學思維由表及里逐漸深入，提升思維的深刻性，讓“定點”在知識鏈中發光發熱。

二、“串鏈”題組練習，讓數學思維由淺入深

“串鏈”題組是對所學知識相關題目的縱向整合，教師可以通過分類、歸納、整理、提煉，把“串鏈”題組分為同鏈同質題組、同鏈異質題組、同鏈遞進題組，避免學生進行沒有頭緒的題海練習，額外增加學生的學習負擔。教師要以分組練習引導學生深入理解數學知識的共性與個性，讓數學思維由淺入深，使數學學習呈現生長態勢。

【題組一】同鏈同質題組

1.甲乙兩人共同完成一項任務，甲自己做需10天，乙自己做需20天，如果兩人合作需要幾天？

2.從教室走到學校圖書館，小明步行需10分鐘，小剛步行需20分鐘，如果兩人同時從兩地相對而行，相遇時需多少分鐘？

同鏈同質題組的特點是構成題鏈的幾道練習內容不同，但解題思路卻相近或相同。如上述兩道工程題，工程題是小學階段考察的重點題型，從分率的方面探究時間、總量和效率三者之間關系，這兩道題內容雖然不同，但解題思路相同：將總量看作單位“1”，用分率表示效率，用單位“1”除以各自的分率，求各自的工作時間。這樣的題組練習可以使學生對認知結構中的相關知識進行融合，拓寬解決某一類題目的思路和方法，提高解題的靈活性。

【題組二】同鏈異質題組

1.一根圓柱形鋼條，底面直徑為8分米，高為20分米，削切成一個最大的圓錐體，削去了多少立方分米鋼材？

2.一根圓柱形鋼條，底面直徑為8分米，高為20分米，加工成一個圓錐體，底面周長為31.4分米，圓錐體的高是多少分米？

同鏈異質題組的特點是構成題鏈的幾道練習題內容相似，解題思路不同，能很好地幫助學生厘清易混題目的表征方式和解題方法。這種題組可以是根據公式的推導順序為線串成題鏈，如可以將小學數學平面圖形的面積計算問題——求平行四邊形面積、求三角形面積、求梯形面積等，串成題鏈。也可以是對某一公式的多方面考察，如題組二，是以圓錐的體積公式及公式變形為線，第一題為圓柱削切成最大的圓錐，已知圓錐的直徑和高求體積；第二題為圓柱加工成最大的圓錐，已知圓錐的體積和底面周長求高。教師還可以引導學生找出這組題中的兩個重要動詞：削切、加工，區別這兩個詞所表達的實際意義，以此為線構成題組。

【題組三】同鏈遞進題組

1.制作雕塑作品，甲和乙合起來需8小時可以完成。如果甲獨自完成需20小時，那么乙獨自完成需幾小時？

2.修馬路，張明工程隊獨自修需30天，劉剛工程隊獨自修需80天。現在由兩隊合作修路，工作14天后，還有1400米沒有完成，這條馬路多長？

3.有一項任務，甲師傅每天作業8小時，3天可以完工；乙師傅每天作業9小時，8天可以完工。如果兩位師傅一起做，每天作業6小時，幾天可以完工？

所謂同鏈遞進，是指構成題鏈的幾道練習內容、解題方法相似，但難度不斷增加。有層次的題組練習，可使學生進一步認識此類問題的結構框架，并在原有認知結構的基礎上繼續豐富，將更多題型納入其中，避免以題練題的情況。

遞進題組的設計是教學中比較常見的，它相當于學生建構認知的“導航儀”，導航的過程就是引導學生分析、解決問題的思考過程。從提供的條件看，遞進題組是從直接條件到間接條件再到隱藏條件的遞進；從計算方法看，遞進題組是加法或減法到連加、連減，再到加減混合的遞進等。相比題組一，題組三中的工作過程相對復雜，工作總量、時間、效率相互轉化，我們可以采用“分干合想，合干分想”的拆并思想。運用分合法來解決，這樣可以幫助學生更好地掌握解題方法，有利于提高練習的實效性。

三、“構面”題組練習，讓數學思維由窄變寬

“構面”題組是把單獨的線性知識進行整合，形成較寬的知識面。“構面”題組應以教材安排的內容順序為線索，通過類比、聯通等方式，將遍布在各年級、單元關聯性較強的知識，進行橫向組織，形成知識面。知識面相較知識鏈而言，更注重數學思想的總結和數學方法的應用，引導學生對相關聯的知識進行歸納、演繹，通過歸納與演繹的雙向互動，實現思維“點—線—面”的輻射式發展，提高思維的靈活性。

【題組一】“構面”題組

1.一個打印小組打印稿件，原計劃每天打印200頁，15天完成任務，實際每天多打印50頁，這份稿件要幾天完成？

2.一個打印小組打印稿件，原計劃每天打印200頁，15天完成任務，實際每天多打印1/4，這份稿件需要幾天完成？

3.一個打印小組打印稿件，原計劃每天打印200頁，15天完成任務， 實際每天多打印25%，這份稿件可提前幾天完成？

該題組第一題是整數應用題，是學生四年級學習的內容，列式為：（200×15）÷（200+50）。第二題是學生五年級下冊學習的分數應用題，列式為：（200×15）÷（200+200×1/4）。第三題是學生六年級上冊學習的百分數應用題，列式為：（200×15）÷（200+200×25%）-12。三道題都要先算出稿件的總頁數，再根據實際每天打印的頁數，求出需要打印的天數。雖然這個題組只是涉及到整數、分數、百分數，但是后面兩道題對于學生來說，關鍵要知道“多的1/4、25%，是指實際每天比計劃每天多打印1/4、25%，多的是計劃每天打印的1/4、25%，用計劃每天打印的加上多的部分，求出實際每天打印的頁數”。三道題涉及到的內容分布在不同年級，由于知識學習的時間跨度較大，小學生處理信息的能力有限，因此學生會出現遺忘的現象。教師將有關聯的信息合理有效地組織成組塊，會增強學生信息加工的能力，使學生站在系統的高度，在整體知識的背景下，對所學的知識進行重構，將知識與方法結成網，減輕其學習負擔。

四、“梳理”題組練習，讓數學應用由點到面

平日復習數的運算時，有些教師往往追求形式化、技巧化，訓練難免單調枯燥，這不僅脫離了學生生活實際，而且挫傷了學生的學習熱情。我們知道，小學生正處于以具體形象思維為主要形式逐步過渡到以抽象邏輯思維為主要形式的階段，尤其是低年級的學生。為此，要基于學生的學習特點來設計本節“運用題組厘清問題層次”的乘除法復習課。

課堂上，我以習題練習為暗線，使學生通過五道基礎題組梳理出已學習的乘除法知識。

1.孫悟空拔出4根毫毛，每根毫毛能變出5只小猴，一共能變出幾只小猴？

2.有12個大桃子，平均分給唐僧師徒4人，每人分到幾個桃子？

3.孫悟空又拿出20根香蕉準備分給小猴子吃，如果每盤放5根，可以放幾盤？

4.小兔有2只，小鹿有6只，小鹿的只數是小兔的幾倍？

5.小兔有2只，小松鼠的只數是小兔的4倍，一共有多少只小松鼠？

這五道題屬于題組圖式中的定點題組，教師在講授數學內容時，要把握這一內容的“定點”，巧用題組練習，讓練習不僅停留在鞏固新知識的層面上，更要啟發學生追溯知識的本質和內核，掌握一組題目的解決方法和蘊含的數學思想。

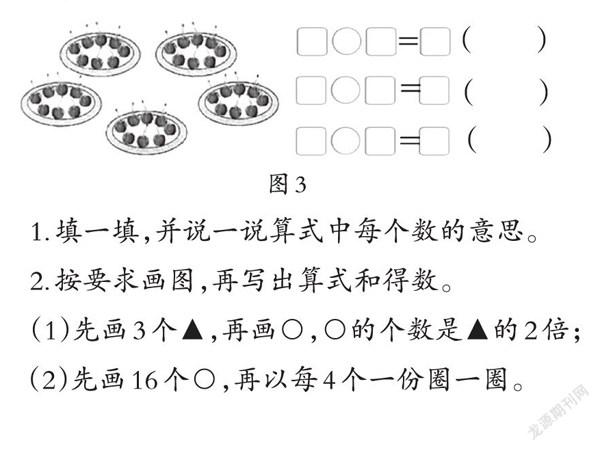
隨堂練習的設置要由易到難，前兩道題是對所學知識相關題目的縱向整合，如圖3，著重考查學生對平均分、倍的認識，以及對乘除法的意義的理解，屬于串鏈題組。

1.填一填，并說一說算式中每個數的意思。

2.按要求畫圖，再寫出算式和得數。

（1）先畫3個▲，再畫○，○的個數是▲的2倍；

（2）先畫16個○，再以每4個一份圈一圈。

而最后一道題綜合考察乘除法的相關知識，是一道開放題，屬于“構面”題組（如圖4）。“構面”題組是把單獨的線性知識進行整合，形成較寬的知識面。知識面較知識鏈而言，更注重數學思想的總結，數學方法的應用，引導學生對相關聯的知識進行歸納、演繹，實現思維“點—線—面”的輻射式發展，解決了作業中存在的機械、無效、重復性等方面的問題。

（1）肉餅的價格是粥的幾倍？

（2）淘氣有10元錢，正好可以買哪些食物？

（3）說一說，你還能提出哪些問題？

“雙減”背景下，要讓習題更有意義，絕不是通過“題海”戰術實現的。本節課結合實際問題生活化的特點，創設學生喜聞樂見的“孫悟空打妖怪”的情境，設置“孫悟空分食物”的活動，貫穿了整堂課，為學生創設角色、情感代入的機會，激發了學生的學習興趣，同時學生的審美興趣、認識興趣、乃至向往豐富精神世界的興趣也在其間培養起來。快樂地解決問題，在給學生留下深刻印象的同時，以題組練習使學生腦海中的認知結構也更加完善。“定點—串鏈—構面”的題組設置，既重視知識練習又重視知識遷移，既關注點狀突破又關注結構完善，既注重縱向聯結又注重橫向整合。有效設計數學題組呼應發展學生思維的訴求，助推其數學思維由表及里、由淺入深、由窄變寬地發展。

參考文獻：

[1]陸李華. 小學數學題組化練習的設計與思考[J]. 遼寧教育，2015（5）.

[2]楊健輝， 楊紹彭. 關注比較過程 實現組合功能——用好數學練習題組的幾點嘗試[J]. 湖南教育， 2012（3）.

（責任編輯：楊強）