優化解題方法，培養理性思維

陳國祥

［摘? 要］ 數學理性思維的發展是提升數學學習能力的基礎，理性思維水平體現為數學思維的靈活性、目標性、發散性和創新性等數學品質. 初中數學教學要以培養學生的理性思維、提升學生的思維品質為目標. 文章提出，通過一題多解的習題訓練，比較不同的解題思路，優化解題方法，能提升學生的思維能力.

［關鍵詞］ 一題多解；解題方法；理性思維；思維品質

數學學習的基礎是思維能力的培養. 學生通過學習數學概念、定理、公式等知識，來提升思維能力，培養思維品質.一題多解的試題訓練，不僅能鍛煉學生思維的靈活性，還能優化學生的思維品質.

本文選取了通過典型試題引導學生嘗試多種解法的教學實踐，與各位同行分享，供大家分析和研究.

呈現典型試題

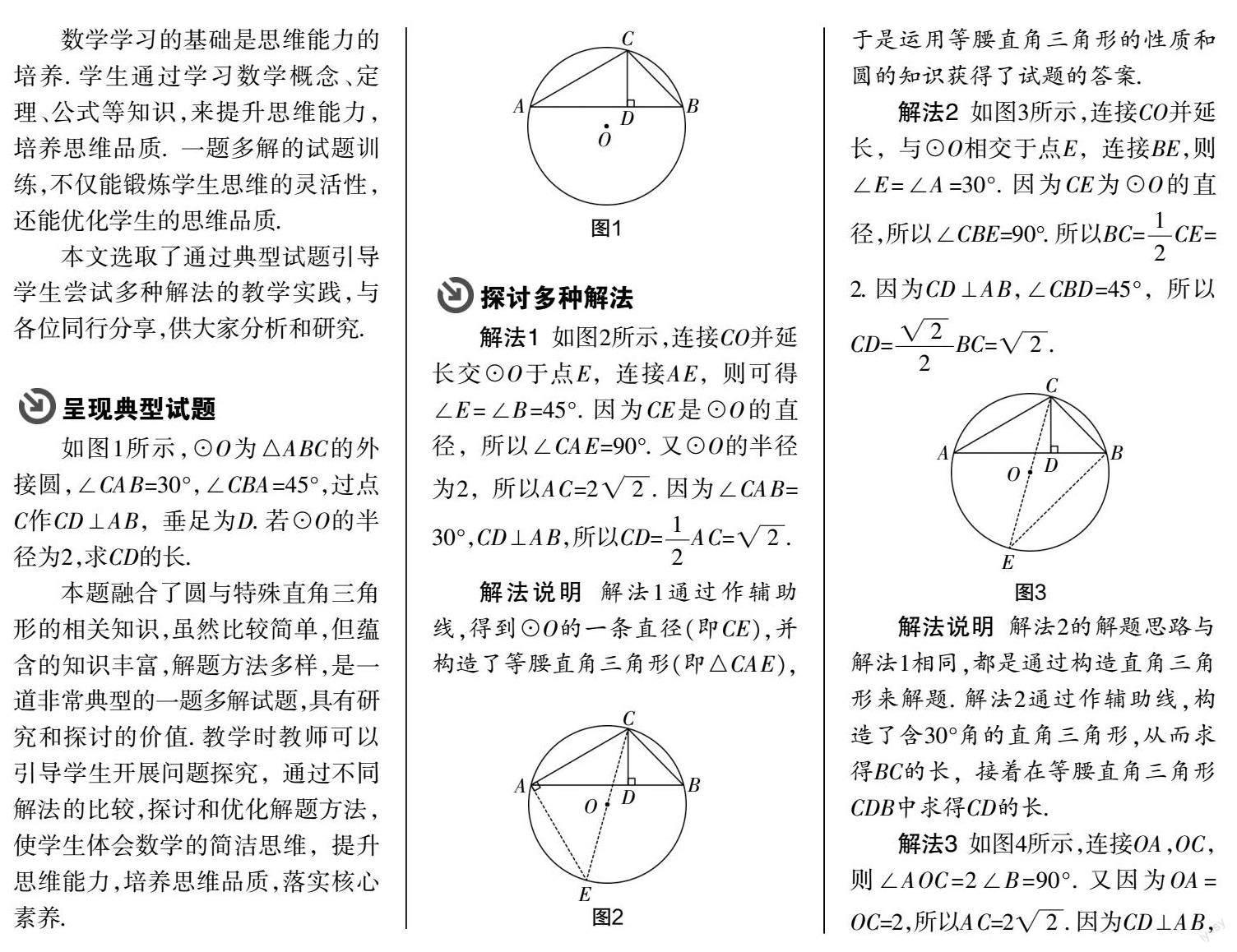
如圖1所示，⊙O為△ABC的外接圓，∠CAB=30°，∠CBA=45°，過點C作CD⊥AB，垂足為D. 若⊙O的半徑為2，求CD的長.

本題融合了圓與特殊直角三角形的相關知識，雖然比較簡單，但蘊含的知識豐富，解題方法多樣，是一道非常典型的一題多解試題，具有研究和探討的價值. 教學時教師可以引導學生開展問題探究，通過不同解法的比較，探討和優化解題方法，使學生體會數學的簡潔思維，提升思維能力，培養思維品質，落實核心素養.

探討多種解法

解法1? 如圖2所示，連接CO并延長交⊙O于點E，連接AE，則可得∠E=∠B=45°. 因為CE是⊙O的直徑，所以∠CAE=90°. 又⊙O的半徑為2，所以AC=2. 因為∠CAB=30°，CD⊥AB，所以CD=AC=.

解法說明? 解法1通過作輔助線，得到⊙O的一條直徑（即CE），并構造了等腰直角三角形（即△CAE），于是運用等腰直角三角形的性質和圓的知識獲得了試題的答案.

解法2? 如圖3所示，連接CO并延長，與⊙O相交于點E，連接BE，則∠E=∠A=30°. 因為CE為⊙O的直徑，所以∠CBE=90°. 所以BC=CE=2. 因為CD⊥AB，∠CBD=45°，所以CD=BC=.

解法說明? 解法2的解題思路與解法1相同，都是通過構造直角三角形來解題. 解法2通過作輔助線，構造了含30°角的直角三角形，從而求得BC的長，接著在等腰直角三角形CDB中求得CD的長.

解法3? 如圖4所示，連接OA，OC，則∠AOC=2∠B=90°. 又因為OA=OC=2，所以AC=2. 因為CD⊥AB，∠CAD=30°，所以CD=AC=.

解法說明? 解法3通過連接OA，OC，構造了等腰三角形AOC，并利用相同的弧所對的圓心角是圓周角的2倍，得到△AOC為等腰直角三角形，最后結合題干條件求解. 解法3同樣是添加輔助線，但與解法1和解法2相比，涉及的知識點更少，因此解題步驟更簡捷.

解法4? 如圖5所示，連接OC，OB，則∠COB=2∠A=60°. 又OC=OB，所以△OCB為等邊三角形. 所以OC=BC=2. 因為CD⊥AB，∠CBD=45°，所以CD=BC=.

解法說明? 解法4與解法3的思路和方法相同，但解法4利用學生最為熟悉的等邊三角形知識，且直接應用了原題中的等腰直角三角形，因此解法4比解法3更加簡捷.

合作探究

引導學生探究出多種解題方法并不是教學的終點，教師還要在課堂教學中引導學生將試題的不同解法進行比較與研究，指導學生在尋求最優解法的實踐體驗過程中實現思維的進階，從一題多解過渡到一題優解，培養學生的創新思維.

師：請大家以小組為單位，結合表1比較這四種解法的區別和聯系.

第一小組：解法1和解法2具有相同的解題思路，都是通過添加輔助線構造直徑，從而形成特殊的直角三角形后求解.

第二小組：解法3和解法4的解題思路是相同的，都是連半徑，形成特殊的三角形后求解.

第三小組：解法4在構造三角形時選擇了等邊三角形，于是可以直接利用題干中已知的圓的半徑得到BC的長度為2，進而通過原題中的等腰直角三角形BDC獲得答案.

師：大家分析得非常好，經過比較，我們發現解法4的解題過程最為簡捷，屬于最優解法.

教學啟示

學習數學要對數學的本質進行探索和理解. 學會解決數學問題并不等同于解數學題，數學教學要引導學生探索數學的本源問題，培養學生的創新能力，使學生能夠從知識的源頭深入理解數學知識的本質，不僅知其然，更知其所以然.

1. 開展解題反思，比較不同解法

解題練習不僅要關注如何獲得解題思路和答案，還要在解題后進行反思，回顧解題的過程，思考解題過程中那些煩冗復雜的部分能否變得更加簡單，并嘗試將較為復雜的部分變得更為簡捷，試著通過直接的觀察就知道整個解題過程. 在學生獨立思考求解和開展多種解題方法交流的基礎上，教師要引導學生回顧獲取解題思路的過程，梳理解題過程中添加的輔助線，并且總結在解題過程中運用的數學基礎知識和解題活動經驗，從而有效地比較不同解題方法之間的本質區別. 這一過程旨在培養學生的深度思維，提升學生的思維能力.

2. 加強思維鍛煉，引導探究學習

教師要引導學生開展自主探究活動，按照學生的認知水平將學生分成若干研究小組，指導學生從不同的角度圍繞學習任務展開探究，并進行研究成果的交流和展示. 教師還要在學生合作探究的過程中進行指導，使學生能夠有條理地對數學問題展開研究和分析，學會從不同的視角理解試題，掌握如何進行不同解法的比較，明晰不同解法之間的優劣，從而為學生開展進一步的數學學習奠定基礎. 研究任務的創建為學生創設了自主學習和交流學習的平臺，營造了輕松愉悅的學習環境，使學生在合作探究中培養了思維品質，提升了合作能力.

3. 開展深度學習，轉變教學方式

隨著課程改革的進行，數學試題不僅關注知識的考查，還關注問題的創新，它們以學生的思維品質為考查目標，突出考查學生思維的靈活性、深刻性和批判性. 因此，教師要主動改革與創新教學方式，擺脫單純的題海戰術、機械練習的教學方式，通過一題多解，引導學生開展合作學習，探討最優解法，學會比較不同的解題方法，鍛煉學生的思維，激發學生的學習積極性，使學生進行深度思考和深度學習. 本例中，教師引導學生合作探究，使他們在交流中迸發出思維的火花，出現不同的解法，并讓他們在相互探討中得到啟發，發現不同解題思路之間的相同之處，從而抓住數學本質，讓數學學習真正發生，使思維真正參與其中.