“雙減”背景下的驅動式數學課堂新樣態

鄭端麗

【摘 要】“雙減”政策對課堂教學提出了更高的要求，高質量常態課堂建設是實施“雙減”的關鍵路徑，要提高常態課教學質量，喚醒學生的學習內驅力至關重要。在數學課堂中，可通過問題驅動、任務驅動、思維驅動的基本策略引發學生深入思考，促進數學知識的深化理解，形成數學課堂新樣態。

【關鍵詞】雙減 驅動 數學課堂

減輕學生負擔，關鍵在于提高課堂教學質量，強化學校教育的主陣地作用，把高質量常態課堂建設作為實施“雙減”的關鍵路徑。那么，應如何提高常態課的課堂教學質量呢？筆者認為教學要先喚醒學生的學習內驅力，基本策略即通過問題驅動引發學生深入思考；通過任務驅動助力學生自主探究、合作交流；在思維驅動中升華提高，促進對數學知識的深化理解。下面以人教版五年級上冊“多邊形的面積”的單元教學為例，探討驅動式數學課堂新樣態。

一、問題驅動——引發真思考

數學課堂總是離不開數學問題的引領，好的數學問題能引領課堂走向深入。有的教師會用幾十個問題，以一問一答的方式，牽著學生跟著預設的教學思路走，學生沒有真正思考的時間和空間，看似配合默契、非常完美的課堂，實則剝奪了學生深度思考的機會。數學教師進行備課時，需要備教材，理解教材的內容、目標、前后聯系；還需要備學生，了解學生的現有知識儲備，對于本節課的學習重難點，教師要做到心中有數；然后才是備教法，針對本節課的教學重點和學生存在的學習困惑，設計行之有效的導學預案。

例如，在教學“三角形的面積”時，對于五年級的學生來說，已具備較強的思維能力和語言表達能力，為了給學生更充分的思考空間，教師不妨設計以下三個問題來引領課堂教學，引導學生層層深入地展開探究。

問題一：平行四邊形的面積公式是怎么推導的？

基于問題驅動，學生回憶前一節課“平行四邊形的面積”的公式推導過程，即通過剪拼的方法把平行四邊形轉化成長方形來計算面積，把新問題轉化成已有的舊知識進行解決。

問題二：三角形的面積可以怎么求？

教師直接把這節課要研究的新問題拋出，學生帶著問題進行獨立思考。學生首先想到的就是利用轉化思想，怎么把未知問題轉化成已知知識來解決。數分鐘后，學生通過分組討論，研究出以下五種計算三角形面積的方法：（1）數格子。這種方法從學生第一次認識面積就已經接觸，它是所有圖形面積計算的基礎，也就是圖形內單位面積的累加。（2）受平行四邊形推導過程的影響，學生把一個等腰三角形沿高線剪開，其中的一部分經過旋轉，拼成一個長方形，由此得出S△=（a÷2）h。（3）把一個長方形沿對角線剪開，三角形面積=長方形面積÷2，由此得出S△=ab÷2。如果沒有提前預習，學生很難想到由兩個完全一樣的三角形拼成一個等底等高的平行四邊形，但有部分學生能想到把一個長方形分成兩個完全一樣的直角三角形。（4）學生會借助常用的學具——等腰直角三角尺來進行拼擺，把兩個完全相同的等腰三角尺拼在一起，形成一個正方形。這樣，三角形面積是正方形面積的一半，由此得出S△=a2÷2。（5）連接三角形兩腰的中點，沿中線剪開，通過旋轉，轉化成平行四邊形，平行四邊形的底即三角形的底，平行四邊形的高是三角形高的一半，由此得出S△=a（h÷2）。學生在小組內分享交流，看似都通過自己的方法解決了問題，正得意之時，教師適機拋出第三個問題。

問題三：這些轉化方法適用于任意三角形嗎？

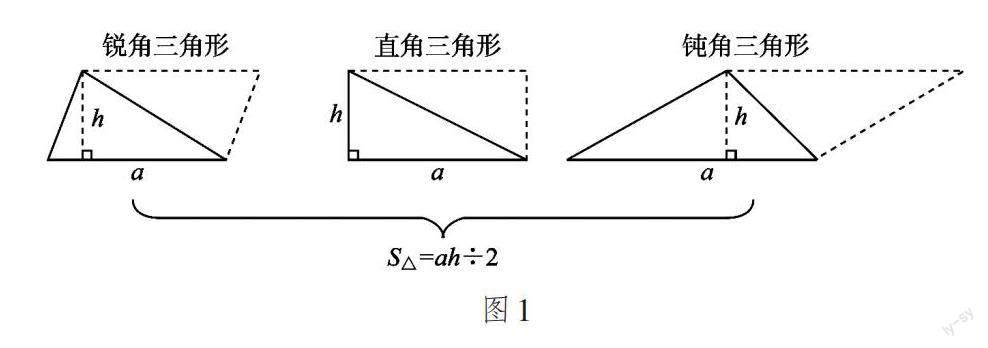
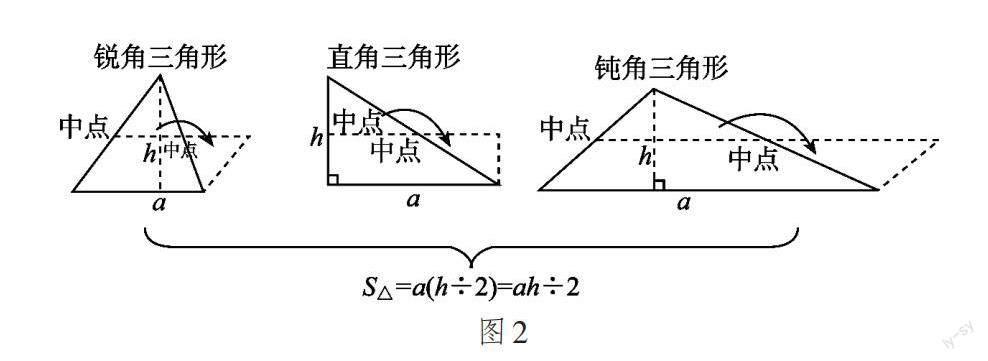
在問題三提出后，學生開始反思自己的推導方式是否適用于任意三角形。教師給予學生充足的思考時間，在這幾分鐘里，學生經歷了思辨—驗證—歸納的學習過程。經過反復辨析、驗證，學生發現方法（1）雖然具有普遍性，但這種方法難以精確地計算出三角形的面積。方法（2）和方法（3）僅限于特殊的三角形，并不具有普遍性。方法（4）中的推導盡管針對的是特殊三角形，但其思路和方法適用于任意三角形（如圖1）。方法（5）同樣適用于任意三角形（如圖2）。

以問題引領課堂，不僅讓學生關注知識的結果，也關注知識形成的過程。學生在思考交流的過程中，感受到數學知識應具備的嚴謹性、普適性和科學性等特點。

二、任務驅動——促進真探究

《義務教育數學課程標準（2022年版）》（以下簡稱《課程標準》）指出：有效的教學活動是學生學和教師教的統一，學生的學習應是一個主動的過程。高質量課堂不僅注重學生積極思考、自主探究，小組合作交流也是數學課堂學習的重要方式。合作交流通常以某個學習任務為驅動，以小組合作的形式進行，在有限的時間內讓學生獨立思考、充分表達、交流辨析、調整修正，學生在交流中碰撞出思維的火花，生長出新的靈感與頓悟。

例如，在教學“梯形的面積”一課時，教師可以根據本節課的教學目標，提煉核心問題，厘清學習任務，以完成導學單的形式開展課堂教學，讓學生在任務驅動下完成數學知識的探究過程。為了節省課堂時間，教師也可以將探究任務提前告知學生，讓學生利用課前時間思考，課堂上可直接進入小組合作、交流互動環節。

教師課前出示任務單：（1）猜想梯形的面積可能與什么有關。（2）探究梯形面積公式的推導方法，請寫出推導過程。（3）小組交流，說說你們的發現。在探究任務（1）時，學生已經掌握了平行四邊形和三角形的面積公式及其推導方法，在已有的學習經驗上，學生匯報自己的猜想：梯形的面積可能與上底、下底、高或梯形的腰有關；梯形的面積可能與平行四邊形、三角形的面積有關。帶著這樣的猜想，學生進入任務（2）的探究。

學生基于已有的知識經驗，利用轉化思想，在研究任務（2）時，有的學生受三角形面積公式推導經驗的影響，把兩個完全一樣的梯形拼成一個平行四邊形；有的學生把梯形通過割補的方法轉化成已學過的圖形，比如把梯形轉化成兩個三角形，或把梯形轉化成一個平行四邊形加一個三角形，或把梯形轉化成一個長方形加兩個三角形等；還有的學生通過閱讀數學材料，學習古代數學家劉徽利用出入相補原理來推導梯形面積公式。這些都是學生通過自主嘗試生成的思維結晶，都是數學中化歸、轉化思想的具體表現。

最后，學生帶著自己的作品進入任務（3），學生迫不及待地分享自己的創作成果，將自己的想法在小組內分享交流，并發現還有很多方法是自己根本沒想到的，由此充分激發了學生的學習興趣，促進了學生思維的生長，增強了學生的創造能力，讓課堂充滿活力。

在各小組匯報的過程中，學生更正自己的導學單，把所有的方法進行統整、梳理，發現梯形面積有多種求法。此時，教師稍加引導“所有的推導方法都能用一個公式表示嗎”，學生的思維進入了更高階段，他們開始推導、轉化，在師生的共同努力下，發現所有的推導結果都能化簡成一個公式S梯形=（a+b）h÷2。

《課程標準》指出：教學活動應注重啟發式，激發學生學習興趣，引發學生積極思考，鼓勵學生質疑問難，促進學生理解和掌握數學的基本知識和基本技能。教師利用導學單，以任務驅動的方式引導學生積極探究，組織學生進行獨立思考—小組交流—說理辨析—各組匯報—知識梳理的學習過程，讓學生全員參與，積極交流，充分說理，讓思維從單點模式向多點模式發展，從而積累數學學習經驗，發展數學學科素養。

三、思維驅動——實現真發展

驅動式數學課堂不僅要求教師要深度解讀教材，準確定位教學目標，把握知識重難點，而且也要關注和順應學生的心理需求，即學生對于一些“數學規定”內心深處有很多的疑惑，教師應追溯知識的根源，巧設思維沖突，在思維驅動下引導學生通過自主探究緊扣數學本質、打破思維定式，對原有的知識結構進行重組，對原有的思維方式重新建構。在這一過程中，讓數學知識得以結構化，學生的思維從表層走向深入。

在“多邊形的面積”整理與復習課的教學中，教師引導學生回顧本單元各圖形的推導過程，當學生說出平行四邊形面積的推導方法，即把平行四邊形沿高線剪開拼成長方形來進行推導時，教師出示特殊的平行四邊形（如圖3），提出問題：像這樣的平行四邊形也可以通過沿高線剪開轉化成長方形嗎？是否能用“底×高”來計算面積呢？教師把問題拋出，引導學生進行思考、交流，從思維進行驅動。

通過教師的追問，各組同學的激烈爭辯，最后能讓學生意見一致的結論是：把平行四邊形分成若干層（高是幾個單位就分幾層），每層均是高為1個單位且面積相同的小平行四邊形，把每層的平行四邊形沿高線剪開轉化成與它等底等高的小長方形后，每層的平行四邊形的面積就轉化成了長方形的面積（具體轉化過程如圖3所示）。把幾個面積相同的長方形的面積進行累加，可以得出平行四邊形面積，即“每層個數×層數=總個數”的方法來計算，也就是“面積=底×高”。接著，教師繼續追問：三角形和梯形的面積也可以用每層個數乘層數來解釋嗎？學生回答：道理是一樣的，因為三角形和梯形每層面積不同，我們要把它拼成每層形狀相同的圖形來計算，可以用兩個完全一樣的三角形或兩個完全一樣的梯形拼在一起計算出總面積，再除以2（如圖4）。

通過充分說理，學生發現求圖形的面積其實就是計算圖形中共有多少個面積單位。從計數的本質看，就是數一數“一行有幾個面積單位，圖形中共有幾行”，這樣面積計算就轉化成了單位面積的累加過程。通過對知識的系統化梳理，學生不僅能掌握本單元的各知識點，還能結構化地理解同一領域內容的內在聯系，從概念本質上理解知識背后的道理，讓學生在思維驅動下深度理解所學知識的本質內涵，有效提升思維素養，實現綜合能力真發展。

（作者單位：福建省福州市倉山小學）