聚焦核心素養(yǎng)　彰顯數學本質

徐健

摘要：豎式計算是計算教學的重中之重，也因其抽象性、過程性，成為小學階段計算教學的難點。教師應聚焦核心素養(yǎng)，彰顯數學本質，依據“去哪里—在哪里—到那里”這樣一個完整的解決問題的思路，對應“目標設定—學情基礎—學習路徑”等環(huán)節(jié)，突破計算教學的難點。

關鍵詞：核心素養(yǎng)；數學本質；計算教學；豎式計算

豎式計算是計算教學的重中之重，也因其抽象性、過程性，成為小學階段計算教學的難點。筆者依據“備‘教—學—評一致性”的理念，遵循“去哪里—在哪里—到那里”解決問題的思路，對應“目標設定—學情基礎—學習路徑”等環(huán)節(jié)，結合北師大版數學教材三年級下冊“隊列表演（二）”一課，談談教學實踐與思考。

一、 目標設定——“去哪里”

基于《義務教育數學課程標準（2022年版）》（以下通稱“新課標”）對“運算能力”的描述，筆者站在大單元的視角梳理了本課的知識結構，并立足核心素養(yǎng)的培養(yǎng)要求，對教材進行了深入解答，在此基礎上，筆者制訂本課的教學目標如下。

1.知識技能：探索兩位數乘兩位數的豎式計算方法，并能正確地進行計算。能結合點子圖、列表格、橫式口算等方式說明乘法豎式中每一步表示的意思，理解算理。

2.數學思考：使學生經歷探索、發(fā)現、總結計算方法的過程，培養(yǎng)學生靈活解決問題的意識和能力。

3.問題解決：能運用兩位數乘兩位數的計算方法，解決一些簡單的實際問題。

4.情感態(tài)度：在運用數學知識和方法解決問題的過程中，體驗數學的價值，感受數學文化及數學在生活中的作用。

二、學情基礎——“在哪里”

教學目標的制訂解決了“去哪里”的問題，接下來，教師要分析學情基礎，找到學生的認知“在哪里”。

三年級學生的思維正處于由形象思維到抽象思維過渡的關鍵時期，仍以形象思維為主。教材安排了利用點子圖探索兩位數乘兩位數的算法，這樣編排的依據是學生在這一階段的認知規(guī)律。三年級學生學習數學，需要有較多的動手操作和直觀表現作為支撐，借助直觀（點子圖）與算式相對應，數形結合。教師要引導學生親身經歷建構兩位數乘兩位數數學模型的過程，這樣不僅能幫助學生理解算理、掌握算法，還有助于培養(yǎng)學生的數感和推理能力。特別是，在教學兩位數乘兩位數（不進位）的計算方法時，教師利用點子圖放手讓學生去探究算法，進而得到乘法算式，不僅使學生經歷了解決問題策略和算法多元化的過程，而且讓學生體會到了乘法算式的簡潔有效，同時滲透了數學思想方法。本節(jié)課和學生以前學習的整數乘法相比，雖然數的位數增加了，計算的過程也變復雜了，但算理算法都具有一致性。即可以按照將數拆分轉化為已學乘法后分別計算再求和，豎式則記錄了“拆、算、合”的過程。教學中，教師要重點引導學生對算理算法進行遷移與運用。

為了更好地了解學生的知識基礎，筆者準備了如下前測題：

1.直接寫得數。

23×3=? ? 14×2=? ?9×8=? ? ? ? ?22×30=

41×200=? ? ?22+160=? ? ? 36+270=

2.列豎式計算。

26×4=? ? ? ?48×6=

3.你會用豎式計算嗎？寫一寫計算過程。

24×33=

第一步：? ? ? ? ? ? ，表示

第二步：? ? ? ? ? ? ，表示

第三步：? ? ? ? ? ? ，表示

通過對前測題的統(tǒng)計，筆者得出如下數據。

準確率：直接寫得數的準確率為96.3%。列豎式計算兩位數乘一位數的準確率為93.2%，兩位數乘兩位數豎式計算的準確率為85.5%，每步的意義三步全對的僅占總數的54.2%。

第3題典型錯誤：第二個乘數33，個位3×24乘得的得數僅有2人出錯，十位30乘24結果有14人算錯，有9人將720的2寫在了個位上，有5人將720的0寫在了個位上。第二步和第三步意義表述不正確的有18人，6人沒有寫。

原因分析：通過預習，學生對兩位數乘兩位數豎式計算有一定的了解，但很多人只是“依葫蘆畫瓢”，對計算算理的理解較為模糊，也不能有效地將算法和算理結合在一起，導致不能準確表述。

三、學習路徑——“到那里”

了解了起點和目的地，下一步我們要思考怎樣“到那里”，就是設計學習路徑。新課標在第二學段“數與運算”的內容要求中提出，探索并掌握多位數的乘除法，感悟從未知到已知的轉化。從未知轉化為已知，能發(fā)展學生的運算能力和推理意識，同時有利于促進學生對算理的理解和遷移。本節(jié)課中，筆者旨在引導學生在理解意義的基礎上運用數形結合、遷移類推、轉化等數學思想方法理解算理、掌握算法。

（一）問題情境，喚醒經驗

本課例在設計和實踐中重視激活學生已有的乘法運算經驗，“隊列表演（二）”和前一課“隊列表演（一）”聯系緊密，在情境設置上一以貫之。所以，本節(jié)課伊始，教師可以延續(xù)前一課的學習情境，引導學生喚醒經驗，讓學生在計算14×12的任務驅動下，回顧兩位數乘兩位數的算理和算法。教師通過點子圖、列表格、橫式口算等方法，將兩位數乘兩位數轉化為學生學過的兩位數乘一位數和兩位數乘整十數，充分喚醒學生的知識經驗。

（二）建立聯系，自主探究

下面從探索算法和融通算理兩方面來說明是怎樣引導學生建立聯系、自主探究的。

1.探索算法

基于前測題的學情基礎，教師大膽放手，讓學生借助學習任務單自主探索兩位數乘兩位數的豎式計算方法。實踐表明，學生能夠遷移之前積累的知識經驗，嘗試用豎式計算出兩位數乘兩位數的結果，在對比、交流、討論的過程中，學生更加完善、統(tǒng)一了兩位數乘兩位數的算法，算理也逐漸變得清晰起來。

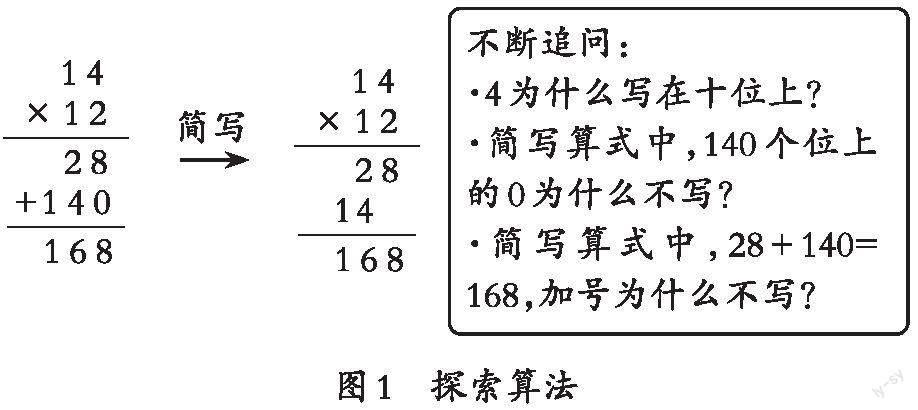
此環(huán)節(jié)，教師備課時應根據學生作答的情況設置兩種預案：一種是收集幾種不同的豎式算法，引導學生進行對比交流，哪里相同，哪里不同，哪種更好？在觀察對比中體會簡便的豎式寫法。另一種是如果學生之前都有知識基礎，不約而同地采用簡便的算法，教師應因勢利導，在學生匯報過程中，就關鍵問題及時地追問：“既然14×10的結果是140，為什么0不寫出來？”“168是表示28和140的和，那這里為什么不寫加號呢？”在課件中用不同顏色將其標出，設計動態(tài)效果不斷閃現，也能使學生認識到如何寫更簡便（見圖1）。

2.融通算理

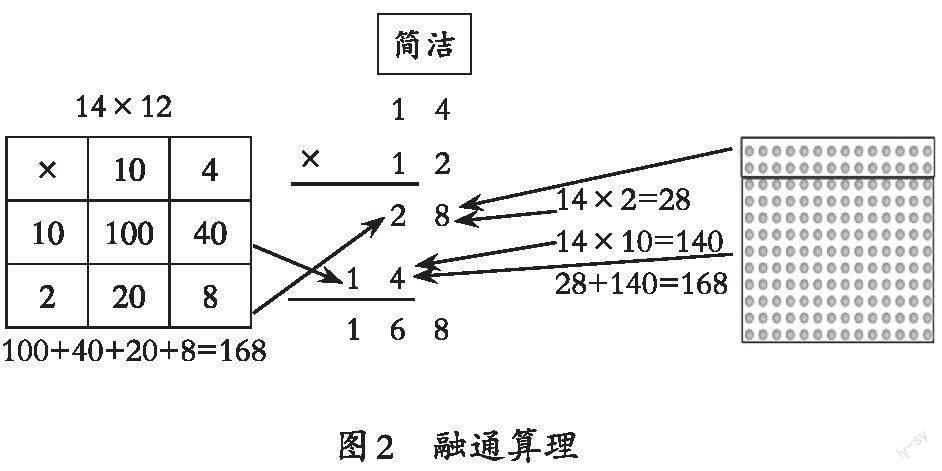
本節(jié)課，教師可先利用對比方法，引導學生多元理解算理。在學生明確豎式的算法和算理之后，教師可引導學生回顧豎式、點子圖、列表格、橫式口算這四種方法的計算過程，提問：它們之間有哪些聯系？然后，教師選派幾名學生直接在課件上連一連，直觀地把各種算法相關聯的部分連在一起，使學生發(fā)現越來越多的關聯。最后，學生恍然大悟，原來這幾種方法形式不同，但算理其實是相通的，都是把數進行拆分，將算式轉化成已經學過的算式，體現了先分后合的數學理念（見圖2）。這個環(huán)節(jié)的設計給學生創(chuàng)造了自主探索的空間，讓學生在生生交流中明確各種方法的共通之處。

（三）構建模型，總結方法

豎式計算實際上就是數位上數字之間的運算，所以要特別理解：每一次數字運算的結果都應該寫在它合適的位置上。這也是理解和掌握豎式筆算的難點和關鍵。在教學中，依照筆者的教學經驗，學生經常出現豎式中第二層的積寫不準位置的現象，這時很多教師往往會繼續(xù)枯燥地反復講，重復練，但因為學生不了解第二層結果錯位寫的道理，硬性地矯正過度反而事倍功半。所以，在本課中，當學生充分理解了各種算法的計算一致性后，教師要梳理歸納：乘法計算就是運用乘法口訣把相同計數單位的個數放在一個方向上合并。教師在豎式上方要板書計數單位，進一步強化分層記錄的合理性，解釋豎式中的對齊方式以及合理落腳之處，要在多個環(huán)節(jié)讓學生反復表述，使其逐步建立起乘法的豎式計算模型，實現從一位數乘法到兩位數乘法、多位數乘法的算法統(tǒng)一。學生在自主探索中經歷知識的生成過程，在探索“怎樣算”“為什么這樣算”的過程中學算法、明算理。教師將“冰冷”的算法和“神秘”的算理融合，并滲透數學思想方法，讓學生清楚地感受“法中見理，理中得法”，學生的運算能力和推理意識也進一步得到發(fā)展。

（四）揭示本質，遷移運用

學生有了大量的算理理解和計算實踐練習積累之后，教師應順勢提煉：當乘數是一位數時，乘積結果只有一層，表示多少個一，當乘數是兩位數時，乘積結果部分有兩層，第一層表示多少個一；第二層表示多少個十；當乘數是三位數時……最后將它們合在一起，其實也就是計數單位的累加。這個提煉讓學生從大單元的視角去審視乘法的本質，而掌握了這個本質，就能夠較好地實現算法遷移。

此外，教師還可鼓勵學生在兩位數乘兩位數計算經驗的基礎上遷移算法，計算三位數乘兩位數、四位數乘兩位數，構建豐富的探索素材，激發(fā)學生的探索動力。

參考文獻：

［1］馬曉麗. “學生問題”催生“學習生機”：記“格子乘法計算原理”的研究小故事［J］ .小學數學教師，2022（1）.

［2］潘麗云. 小學數學教師提升數學史素養(yǎng)的意義與路徑：以“豎式乘法”教學為例［J］.教學月刊小學版（數學），2021（6）.