HPM視角下的“勾股定理”教學設計

王正陽　楊立英　周惠惠　吳新鳳

［摘 要］隨著HPM研究的逐步深入，基于培養目標和核心素養，將數學史、數學文化融入數學課堂的教學研究，已逐漸成為數學教育發展的方向。但是在教學實踐中，仍然存在教師對數學史的知識講解僅停留在介紹層面及忽視數學史在培養學生思維能力和人文素養等方面的作用等問題。文章以“勾股定理”的教學為例，探討HPM理論在數學教學實踐中的應用。

［關鍵詞］HPM理論；勾股定理；教學設計

［中圖分類號］? ? G633.6? ? ? ? ［文獻標識碼］? ? A? ? ? ? ［文章編號］? ? 1674-6058（2023）29-0001-03

近年來，隨著課程改革的不斷深入，我們的教學目標也逐步從“教書”擴展為“育人”，以“立德樹人”為教育的根本任務建設“課程思政”，培養德才兼備、全面發展的社會主義建設者和接班人。數學史融入數學課堂，正是課程思政建設的重要途徑。此外，《普通高中數學課程標準（2017年版2020年修訂）》中也明確指出：“通過數學概念和思想方法的歷史發生發展過程，一方面可以使學生感受豐富多彩的數學文化，激發數學學習的興趣；另一方面也有助于學生對數學概念和思想方法的理解。”

本文選擇義務教育階段的數學課程“勾股定理”一節，在重構勾股定理歷史的基礎上進行教學設計，希望通過對此案例的分析，為將數學史融入教學實踐的內容選擇、融入方式、教學目標以及預期效果等方面的研究提供可行的思路與方法。

一、HPM理論

HPM是History and Pedagogy of Mathematics（數學史與數學教育）的簡稱，其主要研究內容包括數學史與教學法、數學史與學生認知發展規律、基于數學史的教學設計、數學與其他學科的關聯、多元文化的數學等。對HPM研究歷史進行追溯，要從1972年談起。1972年，在第二屆國際數學教育大會上成立了數學史與數學關系國際研究小組，標志著HPM成為一個學術研究的領域。而國內對于HPM的研究，則是從2005年全國第一屆數學史與數學教育會議召開，時至今日，HPM已成為國內數學教育研究的一個重要方向。

汪曉勤教授提出了四種將數學史融入數學課堂的具體方式：附加式、復制式、順應式、重構式。本文以“勾股定理”的教學設計為例，探討將數學史融入數學課堂的方式。

二、勾股定理的歷史及其重構

（一）勾股定理的產生

1.趙爽弦圖

公元前十一世紀，西周數學家商高提出“勾三、股四、弦五”，勾股定理因此得名。而我國對于勾股定理的應用，最早可追溯到大禹治水時期。

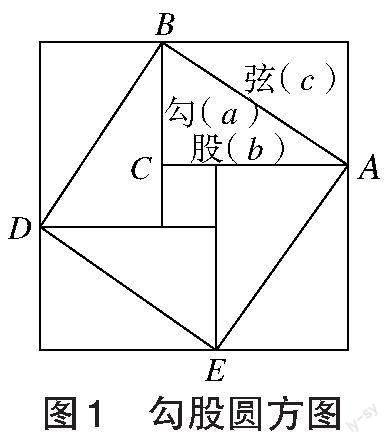
公元三世紀，數學家趙爽在注解數學著作《周髀算經》時提到：“勾股各自乘，并而開方除之，即弦。”趙爽創造了一幅“勾股圓方圖”（如圖1），對勾股定理進行了詳細的證明，后世人們稱之為“趙爽弦圖”。

勾股定理是中國古代數學史上最杰出的成就之一。對于勾股定理的證明，相較于西方的畢達哥拉斯和歐幾里得早了500多年。2002年在北京舉辦的國際數學家大會，也將“趙爽弦圖”作為會徽（如圖2）。

2.畢達哥拉斯定理

相傳2500年前，古希臘數學家畢達哥拉斯在朋友家做客時，發現朋友家用地磚鋪成的地面（如圖3）中反映了直角三角形三邊的數量關系：任意直角三角形，兩直角邊的平方和等于斜邊的平方，即畢達哥拉斯定理。相傳為了慶祝這一發現，畢達哥拉斯學派殺了一百頭牛酬謝供奉神靈，因此畢達哥拉斯定理又稱“百牛定理”。

（二）勾股定理的證明

勾股定理的證明方法有很多種，僅在清朝末年，我國數學家華蘅芳就提出了二十多種勾股定理的證明方法。除上述提到的證明方法外，值得一提的是，美國總統加菲爾德也給出了勾股定理的一種證明方法，通過“兩個直角三角形面積[+]等腰直角三角形面積[=]直角梯形的面積”這一等量關系（如圖4），即可得出勾股定理。

（三）勾股定理的應用

1.直接應用

如圖5所示，[△ABC]和[△DCE]都是邊長為4的等邊三角形，點[B、C、E]在同一條直線上，連接[BD]，則[BD]的長為? ? ? ? ? ? 。

2.實際應用

小莫媽媽買了一部42英寸（約106厘米）的電視機（如圖6）。小莫量了電視機的屏幕后，發現屏幕的長和寬分別為85厘米和64厘米，他覺得一定是售貨員搞錯了，你同意他的想法嗎？你能解釋這是為什么嗎？

解：42英寸的電視機指的是其屏幕對角線長為42英寸（約106厘米），因此，如圖7所示構造直角[△ABC]，[AC=64]，[BC=85]，由勾股定理可得：[AC2+BC2=AB2]，[AB≈106]。

綜上，電視機的尺寸是正確的。

三、“勾股定理”的教學設計

（一）勾股定理的提出與歷史發展

教師利用多媒體展示勾股樹（如圖8），引入勾股定理，提問：它由哪些我們學過的基本圖形組成？這個圖案有什么特別的含義？

學生回答：勾股樹是由大大小小的正方形組成的。

教師帶領學生欣賞數學中的美，激發學生的學習興趣和參與動機，并引導學生總結出組成上述圖案的基本圖形——三個正方形和其圍成的直角三角形。

教師講解：組成這一圖案的基本圖形，其實是在古希臘數學家畢達哥拉斯的朋友家的地板上發現的，這一個圖案使得畢達哥拉斯大受啟發，從而發現了非常著名的畢達哥拉斯定理。

教師通過“地板——畢達哥拉斯定理”這一夸張的設定，激發學生的好奇心和求知欲，進而向學生講畢達哥拉斯發現這一定理的小故事，鼓勵學生敢于思考、勇于發現。

（二）勾股定理的探索及證明

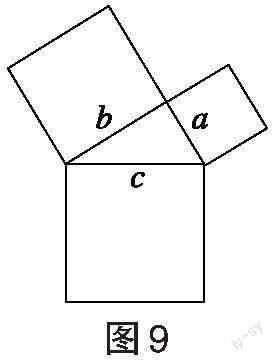
教師提問：如圖9所示，已知直角三角形的兩條直角邊是[a、b]，斜邊長為[c]，猜想一下它的三邊之間有怎樣的數量關系。

學生猜想：[a2+b2=c2]，勾股定理。（通過預習得到）

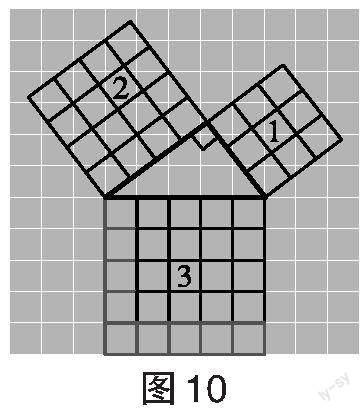
教師提問：將圖9放在方格紙中（如圖10），你能證明你的猜想嗎？

學生證明：正方形1的面積[+]正方形2的面積[=]正方形3的面積。[32+42=25=52]。

教師引導：你能根據剛才的證明過程總結一下勾股定理的內容嗎？

學生總結：直角三角形的兩直角邊的平方和等于斜邊的平方。

教師提問：這樣的一個定理在今天看來是不是特別簡單、容易理解。據說當時為了慶祝這一定理的發現，畢達哥拉斯學派殺了一百頭牛來酬謝供奉神靈，因此這個定理又稱 “百牛定理”。

教師通過引導學生借助方格紙，找到[a、b、c]之間的數量關系，從而證明猜想，并且引導學生用數學語言對這一數量關系進行描述，即勾股定理的內容。

教師提問：同學們有沒有覺得奇怪，明明是畢達哥拉斯發現的定理，為什么要叫作勾股定理呢？現在請同學們拿出你們課前準備的 4 個全等的直角三角形，思考怎樣用這 4 個三角形拼成一個正方形？

學生小組合作，動手操作（如圖11）。

教師講授：其實早在公元前十一世紀，西周數學家商高就提出了“勾三、股四、弦五”，即三邊長分別為3、4、5的直角三角形，這是勾股定理的一種特殊案例。他是最早提出勾股定理的人，勾股定理也因此得名。三國時期，有一位數學家趙爽，畫出了一個和大家一樣的圖形，稱之為“勾股圓方圖”，后世人們把這個圖稱為“趙爽弦圖”。趙爽利用這個圖形，給出了世界上最早的勾股定理證明。既然同學們可以拼出和趙爽一樣的圖案，我相信同學們一定可以用此圖證明勾股定理。

教師提問：還有同學有其他的拼法嗎？

學生展示其他拼法（如圖12）。

教師提問：可以用這個圖形來證明勾股定理嗎？請同學們課后思考。

教師通過引導學生動手操作，對 “趙爽弦圖”的歷史進行重溫，幫助學生更好地理解勾股定理的內涵和證明過程，激發學生的探索欲望，培養學生的實踐能力。同時，介紹我國在勾股定理的證明上早于西方500多年，幫助學生樹立文化自信，培養學生的愛國情懷。

教師講授：美國總統加菲爾德也貢獻了一種非常巧妙的勾股定理證明方法（如圖13），同學們可以試著證明一下嗎？

教師引導學生用多種方法對勾股定理進行證明，培養學生的發散性思維和創新思維，并且鼓勵學生樹立信心，勤于思考，去探索更多的證明方法。

（三）勾股定理的應用

1.如圖14所示，一個梯子[AB]長2.5 m，頂端[A]靠在墻[AC]上，這時梯子下端[B]與墻角[C]的距離為[1.5 m]，梯子滑動后停在[DE]的位置上，如圖15所示，測得[BD]長為0.5 m，求梯子頂端[A]下落了多少米？

解：由題意易知 [AB=DE=2.5]，[BC=1.5]，[BD=0.5]，[CD=2]，

在[Rt△ABC]中，由勾股定理知[AB2=AC2+BC2]，[AC=2]。

[Rt△EDC]中，由勾股定理知[DE2=CD2+CE2]，[CE=1.5]，[AE=AC-CE=0.5]，所以梯子頂端[A]下落了0.5米。

2. 小明家新房裝修，工人師傅搬來了一塊長3米，寬2.2米的薄木板，能順利通過門框（尺寸如圖16所示）嗎？為什么？

解：如圖17所示，連接 [AC]。

在[Rt△ABC]中，由勾股定理知：

[AC2=AB2+BC2]，

因為[AC]大于木板的寬，所以木板能從門框內通過。

數學史融入課堂教學，不單單是講故事，更要講好故事。HPM視角下的數學教學要求教師要在浩如煙海的史學資料中選擇恰當的、有深度的內容，通過對歷史的借鑒、重溫、改編和重構，深入挖掘其中的思想和價值觀念，激發學生的學習興趣，緩解學生的學習壓力，提高學生的數學素養，幫助學生更好地理解知識的內涵和本質。

［? ?參? ?考? ?文? ?獻? ?］

［1］? 楊孝斌，吳萬輝，呂傳漢，等.基于培育數學核心素養的行動：解題課例研析［M］.上海：華東師范大學出版社，2020．

［2］? 張大鵬. 在數學教育中數學史的融入策略［J］. 中國科技博覽， 2015（5）：264.

［3］? 中華人民共和國教育部.普通高中數學課程標準：2017年版2020年修訂［M］.北京：人民教育出版社，2020．

［4］? 汪曉勤，王苗，鄒佳晨.HPM視角下的數學教學設計：以橢圓為例［J］.數學教育學報，2011（5）：20-23.