在生活情境中“創造”概念，在圖形表征中深化本質

摘 要：教學蘇教版小學數學教材《分數的初步認識（一）》單元的第一課時，利用教材例1創設的學生熟悉的“野餐時分食品”的生活情境，從結果能用整數表示到結果不能用整數表示，引發用分數表示的需要，然后引入“分食品”的實物操作，引導學生“創造”分數概念，理解分數表示的結構意義；再利用圖形表征，從直接的到間接的，從面積到長度，從連續的到離散的，設計豐富的外延變式，引導學生應用辨析幾分之一的概念，深化認識其內涵本質。

關鍵詞：小學數學；生活情境；圖形表征；分數概念

*本文系江蘇省基礎教育前瞻性教學改革實驗項目“小學數學個性化教學的實踐研究”（編號：2022JSQZ0126）的階段性研究成果。

一、教前思考

蘇教版小學數學三年級上冊第七單元《分數的初步認識（一）》，是分數知識的起始單元。第一課時主要教學例1和例2：認識一個物體的幾分之一，比較兩個幾分之一的大小。從自然數到（正）分數，是數系的第一次擴充。在自然數概念的基礎上學習分數概念，對學生來說具有一定的挑戰性。

數學來源于對現實世界的抽象。小學生學習數學概念，尤其需要借助生活情境，調動具體（實踐）經驗，理解抽象（理論）知識。同時，根據布魯納的兒童認知發展階段論，也需要經歷從動作表征（實物操作，常常和生活情境相聯系）到形象表征（圖形觀察）再到符號表征（形式化的思考，用來形成抽象知識）的過程，特別需要充分利用具有半具體、半抽象特點的形象表征，作為具體和抽象的中介，實現從動作表征到符號表征的過渡^［1］——形象表征相比于動作表征，還具有便捷、高效的特點，更適合環境相對封閉、資源相對有限的課堂教學。此外，抽象的數學概念具有外延廣泛、內涵明確的特點。學習時，還需要借助豐富的外延變式，通過應用辨析，把握內涵本質。

據此，教學《分數的初步認識（一）》第一課時，筆者設計了兩個環節：在生活情境中“創造”概念、在圖形表征中深化本質。第一個環節，利用教材例1創設的學生熟悉的“野餐時分食品”的生活情境，從結果能用整數表示到結果不能用整數表示，引發用分數表示的需要，然后引入“分食品”的實物操作，引導學生“創造”分數概念（充分體驗分數概念的產生過程），理解分數表示的結構意義，掌握幾分之一的讀寫方法，學會比較幾分之一的大小。第二個環節，利用圖形表征，從直接的到間接的，從面積到長度，從連續的到離散的，設計豐富的外延變式，引導學生應用辨析幾分之一的概念，深化認識其內涵本質。

二、教學過程

（一）在生活情境中“創造”概念

1.創設生活情境，引發用分數表示的需要

師 同學們，通過前兩年的學習，我們初步認識了自然數，知道自然數在生活中很有用，可以表示很多事物的數量。（出示教材例1的情境圖）

兩個小朋友去野餐，他們帶了這樣一些食品。把每種食品平均分成2份，每人分得多少？

生 把4個蘋果平均分成2份，每人分得2個。

生 把2瓶礦泉水平均分成2份，每人分得1瓶。

生 把1個蛋糕平均分成2份，每人分得半個。

師 2和1都是整數；半不僅不是整數，而且不是數。顯然，把1個蛋糕平均分成2份，結果不能用整數表示，那么，結果能用其他的數表示嗎？或者說，我們能創造出其他的數，來表示這一結果嗎？

生 （搶答）

二分之一個。

師 二分之一？怎么寫？

（學生板書：?。）

師 它是一個數嗎？是什么數？

生 分數。

師 你真厲害！你是怎么得到這個數的？

生 書上看到的。

師 那你知不知道分數是怎樣創造出來的？

（學生遲疑。）

利用“野餐時分食品”的生活情境，從結果能用整數表示到結果不能用整數表示，引發用分數表示的需要。這其實是對數學史的重構，符合分數產生的歷史過程，有助于學生理解分數的意義和價值。對于用分數表示半個蛋糕，學生的表現很“真實”：知道二分之一的讀法和寫法，不太清楚分數是怎么創造出來的，歸根到底即不太清楚分數表示的結構意義。

2.組織實物操作，理解分數表示的結構意義

師 老師問得再具體一點：二分之一表示什么意思？

生 把一個蛋糕平均分成2份，每份是它的二分之一。

師 很好！下面，我們實物操作一下，充分體驗分蛋糕的過程，理解二分之一的含義。課前，各個小組的組長給每位組員發了兩個小蛋糕和一把塑料刀。現在，請你拿出一個蛋糕放在盤子里，用塑料刀分一分，并向同桌指出它的二分之一。

（學生活動。）

師 你是怎么分的？二分之一在哪里？

生 這是一個長方形蛋糕，我先用尺子測量它的長度，再從中間的位置用刀將它切成2份。這樣，每份都是2份中的1份，都是它的二分之一。

師 很好！理解了二分之一的含義，你能理解二分之一寫成“?”的道理嗎？下面的“2”表示什么？上面的“1”呢？中間的這條線又是什么意思？

生 從分蛋糕的過程看，中間的這條線表示平均分，下面的“2”表示分的份數，上面的“1”表示所指的對象是其中的1份。

師 表達得真準確！實際上，下面的“2”叫作分母，上面的“1”叫作分子，中間的這條線叫作分數線，它們合起來就是分數。可見，二分之一這么寫非常有道理，分數這樣創造出來也很合理。（稍停）

同樣的道理，如果把一個蛋糕平均分成4份，每份是它的幾分之幾呢？

生 四分之一。

師 很好！請同學們再拿出一個蛋糕放在盤子里，用塑料刀分一分，并向同桌指出它的四分之一。

（學生活動。）

師 很好！你理解了分數的意義。同樣的道理，四分之一該怎么寫呢？

生 寫成“?”。中間的這條線是分數線，表示平均分；下面的“4”是分母，表示分的份數；上面的“1”是分子，表示所指的對象是其中的1份。

師 很好！你掌握了分數的寫法。繼續思考：如果把這個蛋糕平均分成3份，每份是它的幾分之幾？平均分成5份、6份、7份……呢？你能用一句話來概括嗎？

生 把一個蛋糕——

師 只能是蛋糕嗎？

生 哦！把一個物體平均分成幾份，每份就是它的幾分之一。

師 非常好！由分數的產生過程，很容易理解分數的意義，也不難理解分數的讀寫包含自然數成分的道理。

引入“分蛋糕”的實物操作，讓學生“創造”分數概念（充分體驗分數概念的產生過程），理解分數表示的結構意義：由表示平均分的分數線、表示分的份數的分母和表示指的份數的分子組成。從而在充分激發學生學習興趣的同時，幫助學生真正掌握幾分之一的讀寫方法。

3.利用實物操作的結果，學會比較幾分之一的大小

師 認識了幾分之一，能比較一下它們的大小嗎？比如：?和?哪個大？為什么？

生 ?大。我是看出來的：?個蛋糕明顯比?個蛋糕大。

師 很好！學習數學離不開直觀感受。我們還可以進一步感受一下：分別吃下?個蛋糕和?個蛋糕。

（學生吃蛋糕。）

生 一口吃下?個蛋糕噎得慌，一口吃下?個蛋糕比較容易，說明?比?大。

師 很好！不過，學習數學不能只憑感覺，還要講道理。感受過后，你能講講道理，說明?比?大嗎？

生 同樣的蛋糕，分的份數越多，每份就越小；分的份數越少，每份就越大。

師 真了不起！你發現了重要的結論：在分子相同的情況下，分母越大，分數越小；分母越小，分數越大。

生 我還發現，?有2個?大。

師 從分蛋糕的過程可以看出，?和?有這樣特殊的關系。那么，?和?、?呢？

生 ?比?大，?比?大，但它們之間沒有幾倍的特殊關系。

師 是的。之前的結論還是有用的，而它們之間的倍數關系不能用整數來表示——至于用什么表示，后面我們會學到的。

在理解分數表示的結構意義，掌握幾分之一的讀寫方法的基礎上，利用“分蛋糕”實物操作的結果，讓學生比較幾分之一的大小。由此，學生不僅能通過觀察得到結論，而且能通過品嘗加強體驗（增加趣味）。同時，實物操作的結果也有助于學生發現大小關系背后的道理——一般的規律。

（二）在圖形表征中深化本質

1.直接的圖形表征：從面積到長度

師 通過分蛋糕的過程，我們知道了：把一個物體平均分成幾份，每份就是它的幾分之一。現在，把“物體”從蛋糕變成我們學過的幾何圖形。（出示長方形、正方形、三角形、圓各一個）

你能分別找到這些圖形的?嗎？請涂色表示出來。

（學生活動。教師巡視。）

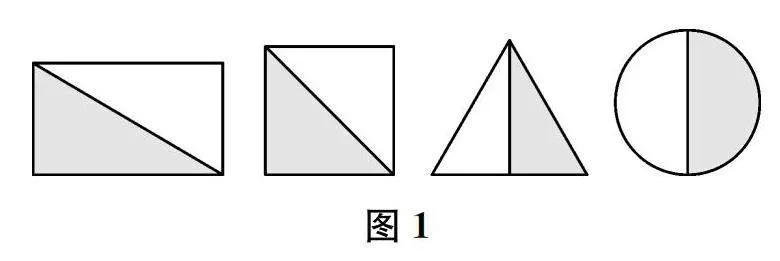
師 （出示學生作品，如圖1所示）

涂色部分的形狀、大小都不一樣，為什么都是相應圖形的?？

生 因為涂色部分都是將相應的圖形平均分成2份后其中的1份。

師 （出示一個正方形）

你能找到它的?嗎？請涂色表示出來。

（學生活動。教師巡視。）

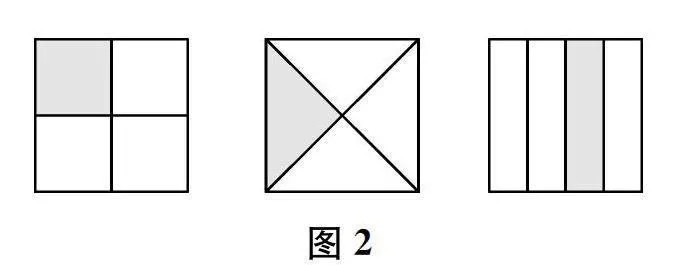
師 （出示學生作品，如圖2所示）

涂色部分的形狀不一樣，為什么都是正方形的?？

生 因為都是將這個正方形平均分成4份后其中的1份。

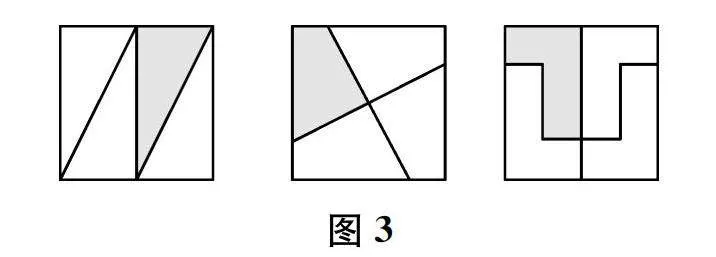
師 很好！你們都抓住了幾分之一的本質：不管什么形狀，只要將它平均分成幾份，每份就是它的幾分之一。（出示圖3）

因此，還可以這樣得到這個正方形的?。

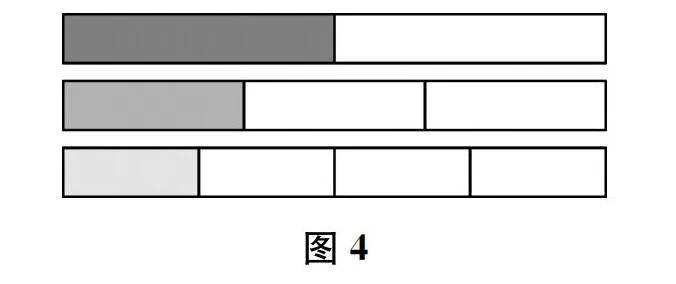
師 （出示圖4）

三個一樣的長方形，估一估：每個長方形中的涂色部分分別是長方形幾分之一？

生 分別是?、?和?。

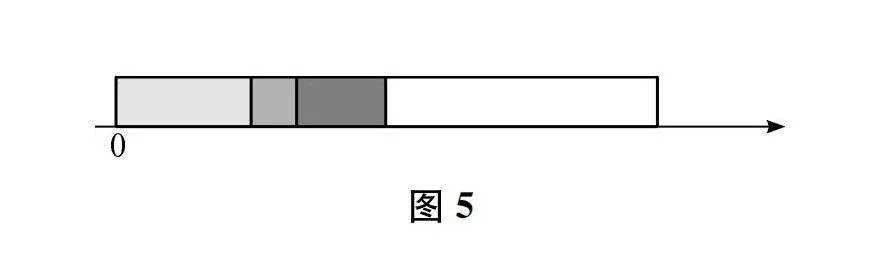
師 這樣的長方形很瘦長，像紙條，平均分時只需要關注長，不需要關注寬。干脆把它們移到一條直線上，讓它們兩端對齊。（出示下頁圖5）

還記得數軸嗎？在一條直線上，原本是一條線段（長度）表示一個數，后來我們找到一個點（位置），假設它表示0，從而在它的一邊，到它距離（與它之間線段長）為1、2、3……的點分別表示1、2、3……這里，我們可以讓三個長方形完全重合，找到重合后圖形的一端，假設它表示0，像圖中這樣，那么，圖形的另一端可以表示什么？三個涂色部分的另一端分別可以表示什么？

圖5

生 圖形的另一端可以表示1，也就是一個長方形的長；三個涂色部分的另一端分別可以表示?、?、?，也就是?、?、?個長方形的長。

師 很好！可見，數軸上不僅有整數，還有分數。以此類推，表示?、?、?、?……的點在哪里？這些點有什么特點和趨勢？

生 這些點都比1小，而且越來越接近0。

師 能到達0嗎？

生 到達不了。

師 它們越來越小，不難理解：分子相同時，分母越大，分數越小。那么，為什么比1小，為什么到不了0？

生 因為分數是把一個物體平均分成幾份，如果原來的物體是1，那么分后的物體肯定比1小；而且不論分成幾份，都不可能沒有大小，也就不可能為0。

師 很好！分數不僅是由整數不夠分得到的，而且可以和整數建立大小關系。抓住了幾分之一的本質，不管是用圖形的面積、長度，還是有關的位置來表示，就都不是問題了。

直接出示圖形，讓學生找到、判斷它的幾分之一。從面積到長度，讓學生在變式應用中把握分數概念的本質。自然地與數軸建立聯系，強化整數與分數的聯系，孕伏整數與分數的大小關系。

2.間接的圖形表征：從連續的到離散的

師 回到現實生活，再看看哪些“物體”中有分數。（出示法國國旗圖片）

這是什么？有分數嗎？

生 法國國旗，它的每一個色塊是它的?。

（教師出示一塊分成8格的巧克力圖片。）

生 巧克力，它的每一個小塊是它的?。

生 還有：它的兩個小塊是它的?，它的四個小塊是它的?。

師 很好！一塊巧克力讓我們想到了這么多分數，接下來就獎勵同學們“吃”巧克力。（出示圖6）

雖然三人吃的巧克力塊數不同，但是都吃了總數的幾分之幾？

生 ?。

師 注意，這里分的不是一個物體，而是多個物體組成的一個整體。同學們很自然地就類比得到了正確結果，很厲害！對于這種情況，下學期我們會進一步學習。

回到現實生活，但是不再提供實物，而是出示表示實物的圖形，也即間接出示圖形，讓學生找到、判斷它的幾分之一。從連續的一個物體到離散的多個物體，讓學生在更多的變式應用中進一步把握分數概念的本質。“離散的多個物體”的幾分之一拓展了分數的概念，為后續教學《分數的初步認識（二）》埋下伏筆。

參考文獻：

［1］俞宏毓，朱向陽，許曉娟.布魯納兒童認知發展階段論指導下的小學數學教學［J］.教育研究與評論（小學教育教學），2024（2）：43.