單元教學，貫通認知

夏菁

【摘要】單元教學是目前教學改革的新形式，重組、建構教學單元成為新的趨勢.但是，更多的是以系統化的數學學科知識與技能為基礎構成的“教材單元”.那么如何設計和建構已有單元的教學，才是一線教師在變革中實際面對的問題.本文以“銳角三角函數”為例，對于單元復習課的設計進行思考，通過三次教學設計的修改，從知識的串聯，到認知的貫通，不斷修改，在加強知識單元復習的基礎上，達到概念貫通和認知圖式建構.

【關鍵詞】 單元教學;初中數學;銳角三角函數

為了真正推進單元教學，復習課的教學設計需要思考：所復習內容和其他知識的關聯是什么？所能形成的數學單元是什么？整個單元中數學邏輯體系、內容主線、知識之間的關聯是怎樣的？

基于實現推進單元教學的復習課設計，本文以“銳角三角函數”單元知識復習部分為例，進行了三次教學設計，反復推敲，進行反思.

評價 這次教學設計，對前兩次設計中的問題進行了改進，問題解決在格點中展開，從“直角三角形”到“斜三角形”再到“無三角形”，最后到“不確定三角形”，將銳角三角函數的基本模型——直角三角形，設計在問題中，從有到無.在學生學習的角度下，逐步深化，從無需構建模型，到自主發現模型，再到自主構建模型，加深了運用直角三角形解決問題的模型意識.

在問題（1）中，借助網格，引導學生判斷三角形形狀，引出直角三角形這一基本模型，并且利用網格特性求出直角三角形兩直角邊長，在求其斜邊長的過程中，自主思考回憶勾股定理.這里其實可以增加開放性問題，讓學生借助網格及圖形，“請你探索該圖形，可以得出哪些量？”喚醒學生認知中對于直角三角形邊與角的思考，再進一步利用勾股定理、銳角三角函數解直角三角形.后面問題（2）中，對于圖形進行簡單變化，看似隱去直角三角形，實則通過前后兩個圖形的對比，解決問題的方法應運而出，學生自然而然的構造直角三角形解決問題.緊接著問題（3）進一步加深這一認識.問題（4）、（5），正式回憶解直角三角形的相關知識，同時圍繞直角三角形，將直角三角形的邊角、勾股定理、銳角三角函數統一構建于直角三角形中，相互貫通.問題（6），加入開放式問題，讓學生自己設計問題，多角度運用銳角三角函數，用數學解決問題.

4 單元復習設計說明與思考

4.1 教學設計從本章知識復習轉向以基本模型為核心的概念貫通

在復習課中，采取單元教學設計，可以更好地貫通概念，凸顯數學概念的本質.以“銳角三角函數”為例，單元復習課的重點，不再只是形式化的設計為：概念復習——典型例題——實際應用——鞏固練習.

為了構建認知單元，在有限的教學時間中，可以優化問題的設置.在“銳角三角函數”的單元教學中，為了凸顯銳角三角函數的基本模型——直角三角形，在最初的教學設計中，可以從直角三角形入手，通過圖形的逐步變化，最后揭示銳角三角函數的基本模型即為“直角三角形”，銳角三角函數解決問題的核心就是構建直角三角形.再通過一系列相關問題的解決，在最后進行總結的時候呈現整體教學問題，幫助學生深化理解，加深認知.

4.2 數學內容從離散、無序的知識點轉向系統有序的認知圖式貫通

知識結構圖能夠將該單元的主要學習內容以及內容之間的關系和結構進行可視化呈現.這種知識結構圖可以更好地梳理相關知識之間的關系，它可以是基本概念、基本方法的簡單陳列，也可以將基本概念和基本方法之間的關系都呈現出來.不同教師單元教學內容的理解不同，知識結構圖的呈現形式也就不同，可以不唯一.但當基本概念、基本方法、基本關系比較復雜時，核心知識地把握就顯得尤為重要，需要明確知識主線.

單元復習教學應該幫助學生優化其內在的知識網絡，而知識結構圖能夠有效地幫助學生形成良好的認知結構，構建整體認知，讓知識像“樹”一樣生長發展.在構建知識結構圖時應該注重以下兩個方面，以便有效提高復習效率，滲透數學核心素養.

（1）注重知識之間的關聯性

復習課不應只著眼于某個單元本身，將相關知識串聯起來，讓學生形成對知識的整體認識，才是單元復習課的關鍵.認知心理學提出數學教學的核心是構建學生良好的認知結構，使之具有不斷吸收新的數學知識的能力和知識不斷發展的能力.

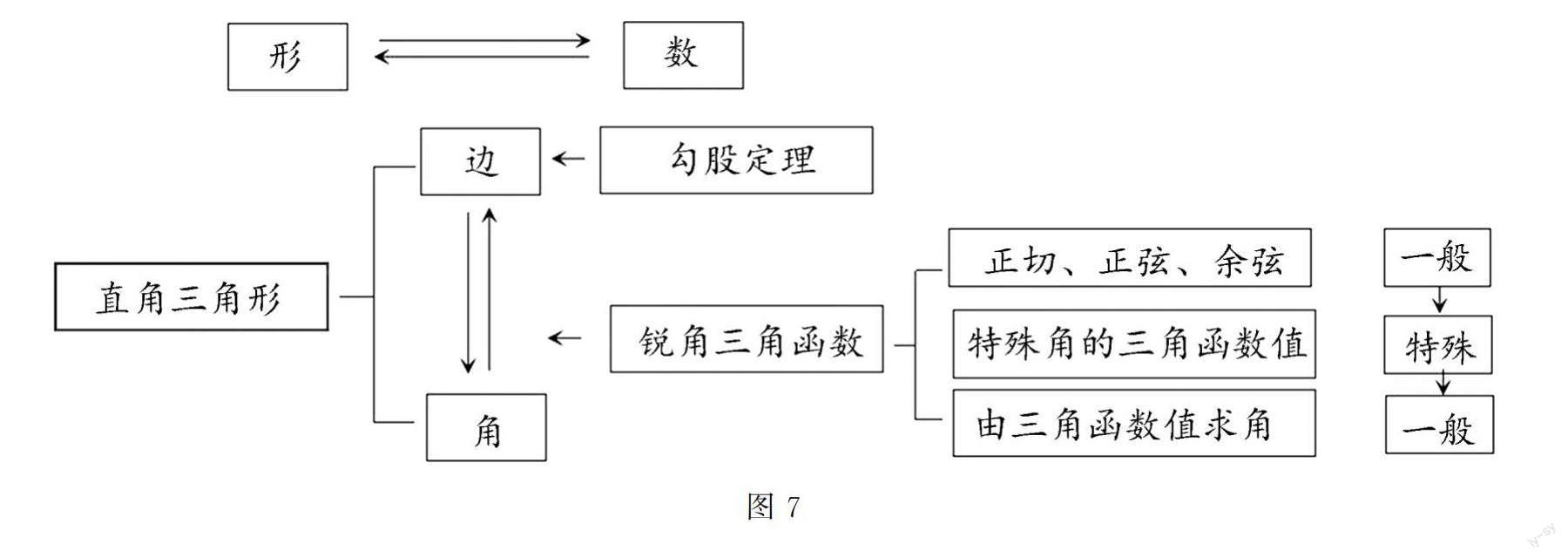
銳角三角函數的復習，從銳角三角函數的概念到特殊三角函數值，再到三角函數值求角，其核心是以直角三角形作為基本模型，將直角三角形的邊角，通過銳角三角函數串聯起來.銳角三角函數的本質，其實是直角三角形邊的比值.問題的解決也應借助直角三角形這一基本模型，并且將相關的勾股定理并入其中，形成統一的認知結構，使銳角三角函數的知識生長于已有的直角三角形相關的認知圖式之上.

（2）注重數學思想方法的滲透

單元復習課也不僅僅是貫通知識本身，更為重要的是加深對其中蘊含的數學思想方法的理解，這是數學學習的精髓所在.數學知識有其系統性，數學思想方法同樣具有系統性，對于思想方法的領悟，也是一個循序漸進的過程.在知識的學習過程中，運用知識解決問題，就需要對數學思想方法進行提煉和總結，一道題變成一類題，一類題變成一種方法，一種方法提煉一種思想，加深學生對基礎知識的理解，有利于學生在已有的知識結構上深化思維，提升素養.

數學幾何的學習，一般包含幾種常見的數學思想方法，如：數形結合、一般與特殊、化歸等.知識結構圖可以適當體現出單元教學中所涉及的思想方法，這是知識與素養之間的紐帶，是學生提升認知的關鍵橋梁.

【本文系江蘇省教育學會“十四五”教育科研規劃課題《認知貫通：初中數學單元教學的實踐研究》（課題編號21A07SXSZ130）階段性研究成果】

參考文獻：

[1]上海市教育委員會教學研究室編著.初中數學單元教學設計指南[M].人民教育出版社，2018.

[2]季洪旭.單元教學探索——基于理解的逆向教學設計案例[M].華東師范大學出版社，2019.

[3]頓繼安等.多維目標單元教學設計與實施（初中篇）[M].北京師范大學出版社，2020.

[4]毛巾鈞.初中數學知識梳理框架圖的教學實踐與研究——以“函數章復習課”為例[J].初中數學教與學，2021（08）：9-12.

[5]王燕燕.單元主題復習設計 引領思維不斷生長——以“銳角三角函數復習課”為例[J].上海中學數學，2018（12）：34-36.