中華優秀傳統文化視域下的小學數學單元整體教學設計

李建良

【摘 要】中華優秀傳統文化在小學數學教學中具有多方面的價值。在教學內容的把握方面，可以為教學順序的確定與核心內容的提煉等提供啟示；在教材內容的分析方面，可以為教材編排的合理性和教學框架設置的科學性等提供參考；在單元整體教學的設計方面，可以為整體目標的制訂及圍繞整體目標的分課時教學活動設計提供方向。文章指出，教師應以嚴格審慎、寧缺毋濫的態度，將中華優秀傳統文化融入小學數學單元整體教學設計與實施的各個環節，促進學生對數學問題本質的深度理解和對傳統文化魅力的深刻體會。

【關鍵詞】傳統文化；多邊形的面積；單元整體教學；小學數學

近年來，隨著《關于實施中華優秀傳統文化傳承發展工程的意見》《中華優秀傳統文化進中小學課程教材指南》等文件的相繼發布，中華優秀傳統文化在教育教學工作中的重要地位日益凸顯，中華優秀傳統文化進校園、進課堂勢在必行。傳統數學文化作為中華優秀傳統文化的重要組成部分，它的教育價值在我國中小學數學教學大綱和課程標準中被多次提及。特別是《義務教育數學課程標準（2022年版）》對此尤為重視，在修訂原則、課程理念、教學建議、評價建議、教材編寫建議等方面都提出了相應的要求。如何有效挖掘傳統數學文化中的素材為數學教學內容的分析提供啟示？如何處理好我國傳統數學文化與現行數學教材內容之間的關系？如何利用傳統數學文化中的精華為單元整體教學所用？這些是中華優秀傳統文化融入數學課堂面臨的主要問題。本文以人教版數學五年級上冊“多邊形的面積”單元教學設計為例展開討論。

一、傳統數學文化對教學內容的啟示

1.關于教學內容順序的啟示

根據“歷史相似性”原理，當前學生數學學習需要經歷的過程，很大程度上與人類歷史上數學知識的發生、發展過程相一致。傳統數學文化中豐富的數學史料，可以為教師設計教學方案、組織教學活動等提供素材和思路。英國數學教師齊利亞克斯基于自己的教學實踐，總結了數學史對于教師和學生的價值，其中的一條是通過數學史獲取引入新知識點的順序。［1］這一價值同樣適用于傳統數學文化。傳統數學文化可以為不同教學路徑的設計提供方向，也可以為某一教學路徑是否具有科學性與合理性提供佐證。

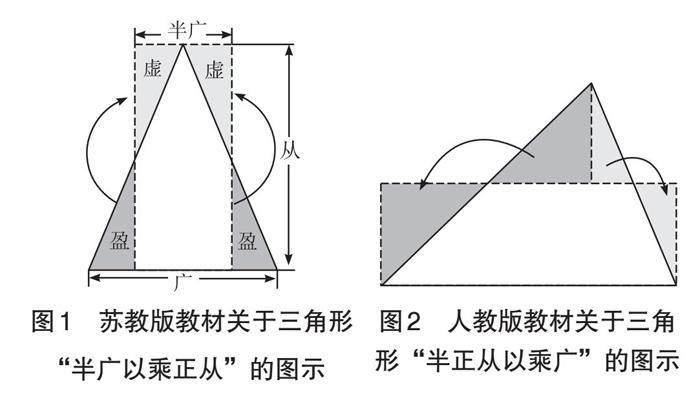
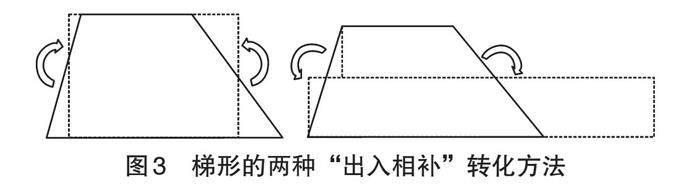
不同版本的教材有關多邊形面積的內容一般遵照平行四邊形、三角形、梯形的順序編排，這是不是唯一的順序呢？《九章算術》中的“方田章”記載了多種平面圖形面積的計算方法，包括方田、圭田、邪田、箕田、圓田、宛田、弧田和環田。其中，除宛田和弧田不屬于小學數學教學內容外，其余基本和小學數學教材中的編排順序一致，即長方形（正方形）、三角形、梯形、圓和圓環，但唯獨少了平行四邊形。查閱其余數學名著，如《孫子算經》《五曹算經》等，也不見有關平行四邊形面積計算方法的記載。那么，少了平行四邊形，是否會影響多邊形面積計算公式推導的邏輯順序呢？《九章算術》中關于三角形面積的計算提到：“圭田術曰，半廣以乘正從。”我國數學家劉徽對其解釋為“半廣知，以盈補虛為直田也”，并提出另一種方法“半正從以乘廣”。蘇教版和人教版數學教材分別對兩種方法進行了介紹并給出圖示（如圖1、圖2）。

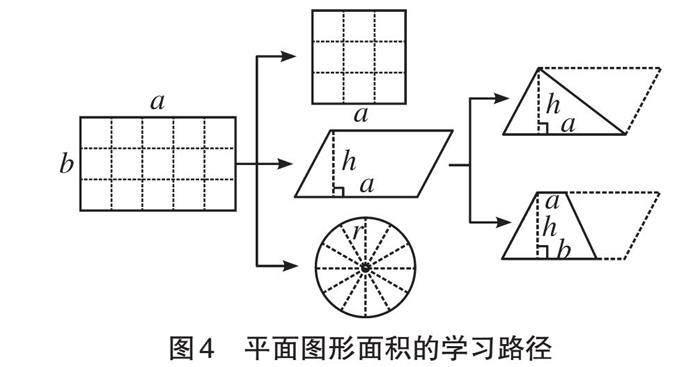
《九章算術》把梯形分為邪田（直角梯形）和箕田（等腰梯形）兩類，兩者的面積計算公式相似，分別是“并兩邪而半之，以乘正從若廣”和“并踵、舌而半之，以乘正從”，即梯形的面積=（上底+下底）÷2×高。另外，梯形面積還有另一種算法：“半正從若廣，以乘并”，即梯形的面積=高÷2×（上底+下底）（如圖3）。

在《九章算術》中，三角形和梯形面積的計算方法是一脈相承的，都是利用了“出入相補”原理轉化成長方形。當然，這一方法也可以用于平行四邊形的面積公式推導。借由傳統數學文化可知，沒有平行四邊形也不影響三角形和梯形面積公式的推導，換言之，平行四邊形的面積并不一定要安排在三角形或梯形的面積之前，它們之間沒有嚴格的先后順序，這就為不同教學順序和路徑的設計提供了依據。

2.關于核心內容提煉的啟示

某一類數學知識在發生、發展和完善的過程中，必然會形成一個核心內容。這個核心可以表現為核心問題、核心知識、核心方法或核心思想等，它揭示了一類問題的數學本質，并貫穿學習的始終。教師能夠抓住核心問題，就能切中要害，達到提綱挈領的效果，使數學教學的難點迎刃而解。傳統數學文化在漫長的發生、發展、鞏固和應用的過程中去粗取精、不斷完善。由此，數學問題的表象逐漸剝離，本質逐漸清晰。這個過程對師生雙方都具有啟發作用，比如能克服常見的主次不分、舍本逐末的弊端，能從中獲得問題研究的視角、思路和方案等。

筆者對人教版、蘇教版、北師大版等版本的數學教材進行梳理和分析發現，各版本數學教材“多邊形的面積”單元基本按照“平行四邊形面積—三角形面積—梯形面積—組合圖形面積—不規則圖形面積”的順序編排。在各版本數學教材六年級下冊總復習中，都通過圖示對平面圖形的學習路徑進行了整理（如圖4）。

從平面圖形面積教學的整體性角度來看，這樣的編排存在一個較大的問題，即忽視了圓的轉化是建立在將圓分割成若干（偶數）個近似三角形的基礎之上的。各版本數學教材“圓的面積”一課中，主要都安排了通過小正方形或網格圖估算圓的面積和通過分割重組的方法將圓轉化成近似平行四邊形（或長方形）兩種方法。但是以上兩種方法之間并不存在直接的聯系，也就是說，圓是很難直接轉化為長方形的。并且，教材前期并沒有相關的鋪墊，學生又如何能想到將圓分割成若干個近似三角形呢？通過對《九章算術》及劉徽注釋的研究，郭書春認為，劉徽的面積理論是一個以長方形面積為出發點，以三角形面積為核心，運用“出入相補”原理和無窮小分割方法的有機整體。［2］陳敏、許含英認為，平行四邊形、梯形都可通過對角線分成兩個三角形，因此可以用三角形面積計算公式來導出平行四邊形與梯形面積的計算法則。最后，可將圓無限細分成近似三角形，再同樣以三角形面積之和來求圓的面積。［3］既然圓的面積研究繞不開三角形，而三角形又是直線圖形中最基本的圖形，那么，何不未雨綢繆，在“多邊形的面積”單元中，就確立以三角形的面積計算方法為核心，來推導其他圖形的面積公式呢？因此，在長方形面積計算方法的基礎上，以三角形的面積計算方法作為平面圖形面積體系的核心展開學習也是值得嘗試的。

由上可知，傳統數學文化在漫長的歷史中，經歷了實踐的檢驗，形成了自己的體系，為教師提煉單元核心內容提供了視角，也為核心內容的準確性提供了依據和保障。

二、傳統數學文化與現行數學教材的關系

1.基于傳統數學文化視角的教材內容分析

在整體教學思路上，教材的編排遵循螺旋式上升的規律，但具體到每個課時，往往是各有側重的。教師在對教學內容進行分析與設計時，如果不能把握現象背后的數學本質，那么在對單元核心的把握上容易出現問題，從而導致看似面面俱到，實則各行其是的不利局面。如果教師對傳統數學文化或相關的數學史料具有充分的了解、認知和理解，則能更好地根據數學發展的規律把握全局，在提煉單元核心的基礎上，使教學設計的歷史序、邏輯序和認知序更好地融合。

現行教材大多將平行四邊形的面積置于單元的第一課時，隨后，主要通過“倍拼法”將三角形和梯形轉化成平行四邊形來推導它們的面積公式。但這種方法無法體現平面圖形的“運動不變性”這一重要屬性，反之，“出入相補法”與“運動不變性”的關系非常緊密。因此，采用“出入相補法”推導面積公式，更能充分體現三角形作為平面圖形面積研究的出發點的地位和作用。那么，如果要嘗試以三角形為核心推導其余平面圖形的面積公式，又需要哪些知識、技能、方法和原理的支持呢？顯然，以“出入相補”原理為依據的圖形分割、運動是重要的一面。另外，還需要用到“等底等高的三角形面積相等”這一規律。大多數教材都沒有將“等底等高”規律作為一個獨立的內容來學習，一般把相關的問題編排在練習課中，目的是利用“等底等高”規律解決圖形面積計算的相關問題，促進圖形之間的一致性認知和理解。但是，這一規律的一個重要價值——在將多邊形分割成三角形的基礎上，通過運動變換，借助“等底等高”規律合并成大三角形，通過類比推導多邊形的面積公式沒有得到充分發揮。

因此，如果確立以三角形面積作為多邊形面積學習的核心，則能充分將“出入相補”原理與“等底等高”規律融為一體，凸顯圖形面積的本質屬性，更好地體現數學學習的整體性與一致性。

2.融合多種元素的單元教學路徑架構

傳統數學文化有其獨特的價值和魅力，但傳統數學文化進課堂，并不排斥外國數學文化的引入。多元文化進課堂，能使學生在古今對照、中外對比中，更好地理解數學的本質，更多地了解世界文化，更好地感悟傳統數學文化的獨特魅力。［4］而要更好地發揮傳統數學文化的價值，必須將其與數學教材內容及常用方法等多種元素進行有效關聯和整合。

將“出入相補”原理與“等底等高”規律有機融合，既能體現圖形的“運動不變性”屬性，又能確立以三角形面積計算方法為核心的多邊形面積計算公式推導體系，同時還能兼顧長方形面積這一基礎，并將多邊形面積公式的推導方法和過程推廣到正多邊形，為后續圓面積的學習提供思路和方法，幫助學生對平面圖形的面積公式推導形成更為整體、一致的認知與理解。基于對傳統數學文化的整理、解讀，以及對現行教材的分析和重構，我們可以把多邊形的面積體系看作一棵小型的“結構樹”。其中，長方形（正方形）的面積是根本，三角形的面積是主干，平行四邊形、梯形、組合圖形（正多邊形）的面積，包括后續圓的面積，都可以看作分枝（如圖5）。有了這棵“結構樹”，“多邊形的面積”單元教學的路徑就變得清晰且具有可操作性了。

三、融入傳統數學文化的單元整體教學設計

單元整體教學最本質、最關鍵的應該是基于“大單元”或“系列單元”的視角，打破自然單元之間和課時之間的壁壘，提煉單元核心概念，圍繞核心概念，提出單元核心問題，以核心素養為目標進行整體設計。［5］傳統數學文化兼具門類齊全、脈絡清晰、知識豐富、方法多樣、思想深刻、體系完備等特點。在數學教育教學活動中，相較于單課時教學而言，將傳統數學文化運用于單元整體教學活動，更能發揮其重要價值。根據單元整體教學的特點和實際需求及傳統數學文化的育人價值，教師可以通過搜集與整理、篩選與解讀、分析與關聯、設計與融合等環節，制訂教學目標，調整教學內容，形成單元整體教學設計。

筆者通過對“多邊形的面積”單元進行素材整理、核心聚焦、教材分析與路徑構架，形成了單元整體教學目標：（1）以長方形面積公式為基礎，以三角形面積公式為核心，探索并經歷多邊形面積計算公式推導的過程；（2）綜合運用多種知識、結論、方法、原理和規律，借助統一路徑，探究并得出各類多邊形的面積計算公式，并體會它們之間的關系；（3）了解傳統數學文化，體會傳統數學文化的魅力，感受傳統數學文化與現代數學方法相結合的巨大推動力。

圍繞核心內容，本文將“多邊形的面積”單元的內容進行了適當的調整，主要是四個方面：一是將三角形的面積調整為第一課時，以便平行四邊形和梯形都能轉化為三角形進行公式推導；二是根據平行四邊形與梯形都能分解成兩個三角形再組合成大三角形的特點，將平行四邊形與梯形的面積合并為一個課時；三是在組合圖形中融入正六邊形面積的研究，讓學生進一步體會“出入相補”原理和“等底等高”規律的運用價值；四是考慮到不規則圖形的面積與單元核心內容之間的關系比較疏遠而暫時未將其納入單元整體教學中來。

因此，本文研究的內容主要包括“三角形的面積”“四邊形的面積”和“多邊形的面積”三個課時（見表1）。在第一課時中，教師主要借助網格圖，鼓勵學生從長方形與直角三角形的面積的兩倍關系及“出入相補”（移多補少）兩個角度推導出直角三角形的面積公式，并將“出入相補”的方法推廣到銳角三角形和鈍角三角形面積公式的推導。另外，在運用面積公式計算等底等高的兩個三角形面積的過程中，教師引導學生體會等底等高的三角形面積相等的規律，使學生能運用該規律解決等高不等底和等底不等高兩類變式問題，加深對上述規律的理解。在第二課時中，教師在喚醒學生多邊形內角和探究方法和經驗的基礎上，引導學生嘗試將平行四邊形分割成兩個三角形，并通過“等底等高”規律或乘法分配律來推導平行四邊形的面積公式。隨后將平行四邊形的面積推導過程遷移到梯形中，推導出梯形的面積公式。當然，這兩種四邊形也均可采用出入相補法轉化為長方形進行面積公式推導。此外，學生還需結合三角形、平行四邊形、梯形的面積公式推導過程和結果，感受三者之間的聯系和互相轉化的途徑，將“等底等高”規律推廣到多種平面圖形中。在第三課時中，教師在常見的組合圖形問題解決的基礎上，加入箏形和正六邊形，從不同角度運用“出入相補”原理和“等底等高”規律解決兩者的面積計算問題，并得出正六邊形的面積公式S=C×h÷2，為后續圓的合理分割及圓面積公式的推導奠定基礎。

將中華優秀傳統文化用于核心問題的分析與提煉、教材內容的調整與關聯、教學路徑的設計與實施，能對實現整體單元教學目標起到積極的推動作用。在借助傳統數學文化開展教學設計的過程中，教師應秉持嚴格審慎、寧缺毋濫的態度，在有理有據的前提下，將中華優秀傳統文化與數學學科發展前沿、數學教育教學最新理念相結合，進行大膽的教學創新。在此過程中，特別要發揮傳統數學文化在單元整體教學中提供整體視角、聚焦核心問題、整合學習素材、達成一致理解的價值，使學生有更多的時間和機會浸潤在傳統數學文化之中，從而促進學生對數學問題本質的深度理解和對傳統文化魅力的深刻體會。

參考文獻：

［1］汪曉勤. HPM：數學史與數學教育［M］. 北京：科學出版社，2017．

［2］郭書春. 古代世界數學泰斗劉徽［M］. 濟南：山東科學技術出版社，1992.

［3］陳敏，許含英. 三角形和梯形面積教學研究［M］. 北京：教育科學出版社，2014.

［4］岳增成，陳梓欣，林永偉. 中華優秀傳統數學文化進課堂：價值、標準與路徑：以“出入相補原理”為例［J］. 小學教學（數學版），2022（4）：4-7.

［5］金嵐. 核心概念統領下的小學數學單元整體教學實踐研究：以“圖形的測量”單元為例［J］. 吉林省教育學院學報，2022（5）：75-79.

（責任編輯：羅小熒）