核心素養視角下2024年全國新高考適應性測試數學試題難度評析與備考啟示

文尚平 農雅婷 盧玉琦 楊璧華

作者簡介：文尚平，1983年生，廣西桂林人，在讀博士研究生，高級教師，研究方向為中學數學課程與教學論；農雅婷，1986年生，廣西崇左人，本科，學士，一級教師，研究方向為中學數學教育教學；盧玉琦，1987年生，廣西賓陽人，本科，學士，一級教師，研究方向為中學數學教育教學；楊璧華，1984年生，廣西南寧人，本科，學士，高級教師，研究方向為中學數學教育教學。

摘 要：2024年全國新高考適應性測試試題的命題風格、試卷結構、難度系數、綜合素養水平代表著高考改革的趨勢和方向，將在2024年新高考中全面體現。課題組借助喻平的數學關鍵能力評價框架和鮑建生的綜合難度系數模型，分別對此次適應性測試試題所蘊含的數學核心素養水平和試題的綜合難度進行分析，探尋兩者之間的內在關系，通過對新高考命題的趨勢、特點等開展實證研究，提出備考啟示：深化基礎，強化對數學學科本質的理解；注重素養，強化對數學教育內核的追求；改善教學，強化對數學思維能力的培養。

關鍵詞：數學核心素養；綜合素養水平；綜合難度系數；適應性測試

中圖分類號：G63 文獻標識碼：A 文章編號：0450-9889（2024）08-0053-06

《普通高中數學課程標準（2017年版2020年修訂）》（以下簡稱《課程標準》）系統提出了六大數學學科核心素養及水平的劃分，明確了數學學科核心素養是數學課程目標的集中體現，拉開了數學學科核心素養從理念層面走向教學實踐的序幕，并將數學科核心素養的培養貫穿新教材、新課程和新高考“三新”綜合改革的全過程［1］。2019年，《中國高考評價體系》明確提出高考命題要突出考查學生的必備知識、關鍵能力及學科思維，以核心素養為導向的基礎教育考試評價日益成為社會關注的焦點。核心素養的測評是以區分度為主要依據開展的，而試題的區分度與試題的難度又有著緊密的聯系。基于上述分析，筆者認為一線教師有必要研究試題難度與核心素養之間的有機聯系。

2024年，全國第四批高考綜合改革省區將要首考落地，新高考試題將如何有效開展學生數學學科核心素養的測評？試題的區分度與試題的難度將發生怎樣的變化？對這些問題答案的追尋，需要結合2024年1月舉行的全國九省區新高考適應性測試數學試題進行。那么，此次適應性測試數學試題每一道題的具體難度系數是多少？試題的綜合素養水平如何？試題的綜合素養水平與綜合難度系數的關系怎樣？本研究借鑒了喻平提出的數學關鍵能力評價指標框架和鮑建生提出的綜合難度系數模型，對2024年全國九省新高考適應性測試數學試題進行評析，并基于研究結果得出相應的備考啟示。

一、研究設計

（一）研究對象

2024年，廣西、吉林、黑龍江、安徽、江西、貴州、甘肅將作為第四批高考綜合改革省區進入新高考模式。為實現平穩過渡，2024年1月19—21日，全國九個省區組織開展了高考綜合改革適應性測試演練，其中數學試題由教育部教育考試院命制。此次演練具有明確的方向性，且數學測試卷變化非常大，引發了社會的強烈關注。因此，本研究選取該試題作為研究對象具有非常重要的現實意義。

（二）研究工具

數學學科核心素養的測評主要以試題區分度為依據，而試題區分度與綜合難度相關［2］。為了更直觀地分析試題的綜合素養水平與綜合難度之間的關系，本研究采用喻平的數學關鍵能力評價指標框架并參考了鮑建生的綜合難度系數模型對此次適應性測試卷進行量化研究。

1.試題核心素養水平的量化

（1）數學關鍵能力評價指標框架

《課程標準》提出了數學學科“數學抽象、邏輯推理、數學建模、直觀想象、數學運算和數據分析”六大核心素養，并對所有素養進行了三級水平的劃分。然而，由于六大核心素養定義的抽象性，導致在對具體數學試題進行素養劃分操作中遇到了困難。為解決數學試題中核心素養水平劃分的操作性問題，本研究采用喻平的數學關鍵能力評價指標［3］（如表1所示），對適應性測試題的核心素養水平進行實踐性劃分。

表1 數學關鍵能力評價指標框架

[關鍵

能力 知識理解

（水平1） 知識遷移

（水平2） 知識創新

（水平3） 數學

抽象 理解試題的基本概念、規則 在實際情境中

抽象數學問題 抽象出新概念、命題、方法 邏輯

推理 掌握推理的基本形式和規則 可以驗證結論或發現簡單結論 能發現、驗證、解決復雜問題 數學

建模 掌握基本、常規的數學模型 能在具體情境中建立數學模型 能用多種知識、方法建立模型 直觀

想象 了解基本圖形的性質、特點 能利用圖形研究數學問題 構建數學問題的直觀模型 數學

運算 理解基本運算的規則 能用多個規則

進行綜合運算 設計運算程序、解決復雜問題 數據

分析 掌握基本的

數據處理工具 能用常規方法

分析試題中數據 構建模型、方法進行數據分析 ]

（2）試題綜合素養水平

將試題蘊含的核心素養量化，即為試題綜合素養水平，試題所蘊含的核心素養水平越高，綜合素養水平也相應越高［4］。為了得到每一道試題蘊含的綜合素養水平，首先需要對核心素養的每一級水平進行賦值（量化），考慮到區分度因素，將表1中核心素養的水平1、水平2、水平3分別賦予1、3、7的分值（權重）。其次利用綜合素養模型公式d=[nidijn]，i=1，2，…，6，j=1，2，…，計算試題的綜合素養水平。（公式中d代表綜合素養水平，n代表試題總數，ni代表蘊含核心素養i的題目數量，dij代表核心素養i的第j級水平的賦分值）

2.試題綜合難度的量化

（1）綜合難度模型

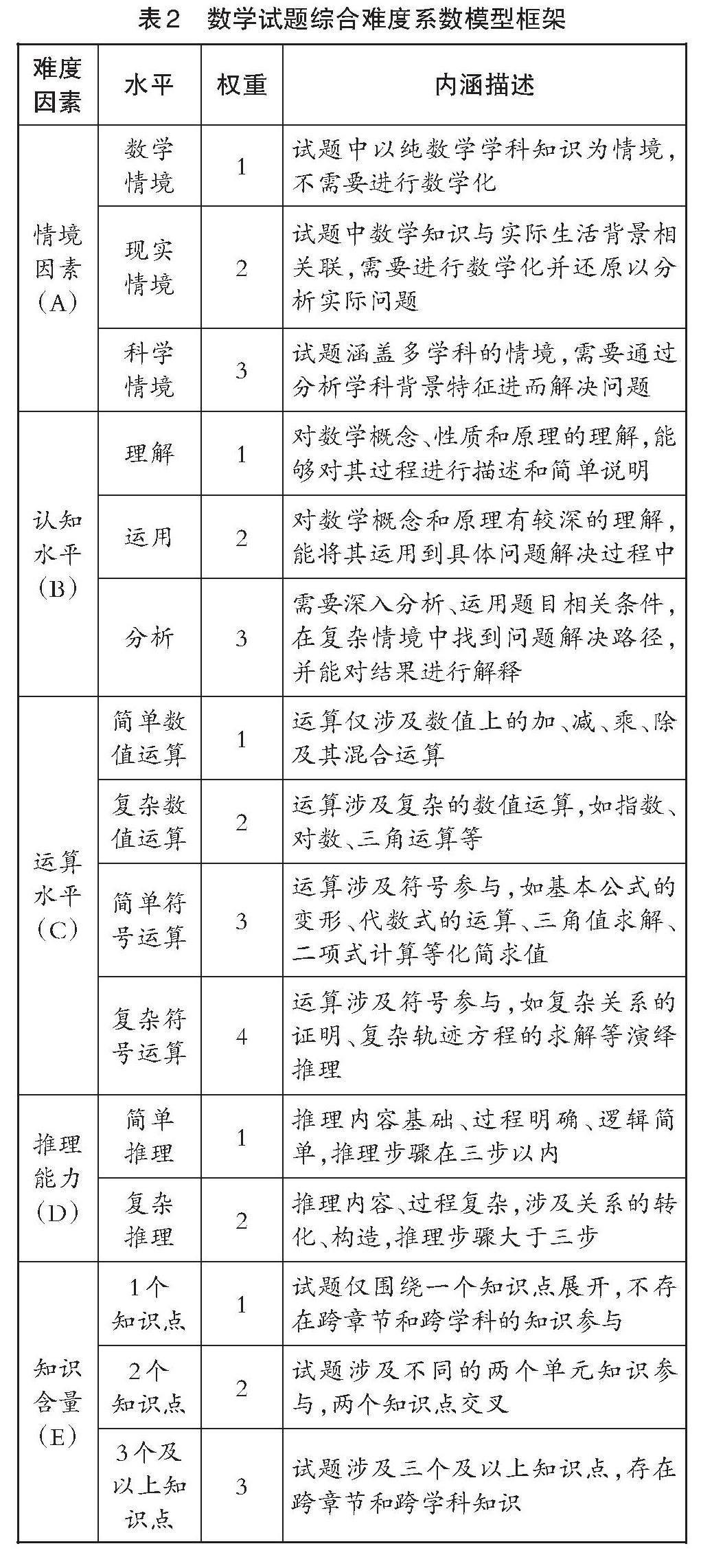
試題難度是衡量該試題對被試者全體的適合程度，數學試卷綜合難度是指數學試卷的內容、結構妨礙學生完成答卷的阻力程度［5］。為了較好地反映此次測試卷的難度水平，本研究參考了鮑建生提出的綜合難度模型［6］，依據該模型的情境、認知、運算、推理以及知識含量等五個難度因素及其水平描述（如表2所示），對適應性測試卷試題難度進行實踐性劃分。

表2 數學試題綜合難度系數模型框架

[難度

因素 水平 權重 內涵描述 情境

因素

（A） 數學

情境 1 試題中以純數學學科知識為情境，不需要進行數學化 現實

情境 2 試題中數學知識與實際生活背景相關聯，需要進行數學化并還原以分析實際問題 科學

情境 3 試題涵蓋多學科的情境，需要通過分析學科背景特征進而解決問題 認知

水平

（B） 理解 1 對數學概念、性質和原理的理解，能夠對其過程進行描述和簡單說明 運用 2 對數學概念和原理有較深的理解，能將其運用到具體問題解決過程中 分析 3 需要深入分析、運用題目相關條件，在復雜情境中找到問題解決路徑，并能對結果進行解釋 運算

水平

（C） 簡單數

值運算 1 運算僅涉及數值上的加、減、乘、除及其混合運算 復雜數

值運算 2 運算涉及復雜的數值運算，如指數、對數、三角運算等 簡單符

號運算 3 運算涉及符號參與，如基本公式的變形、代數式的運算、三角值求解、二項式計算等化簡求值 復雜符

號運算 4 運算涉及符號參與，如復雜關系的證明、復雜軌跡方程的求解等演繹推理 推理

能力

（D） 簡單

推理 1 推理內容基礎、過程明確、邏輯簡單，推理步驟在三步以內 復雜

推理 2 推理內容、過程復雜，涉及關系的轉化、構造，推理步驟大于三步 知識

含量

（E） 1個

知識點 1 試題僅圍繞一個知識點展開，不存在跨章節和跨學科的知識參與 2個

知識點 2 試題涉及不同的兩個單元知識參與，兩個知識點交叉 3個及

以上知

識點 3 試題涉及三個及以上知識點，存在跨章節和跨學科知識 ]

（2）試題綜合難度系數

為了得到每一道試題的綜合難度系數，首先需要依據綜合難度模型對五個難度因素進行編碼賦值，再將編碼后的數據代入公式fi=[jnijfijn]，[jnij]=n，i=1，2，…，5，j=1，2，…，計算各試題的難度系數fi。（公式中[nij]表示第i個維度第j個水平的題目數，[fij]表示第i維度第j水平的權重，n表示題目總數）

二、2024年全國適應性測試數學試題的綜合素養水平和綜合難度分析

為了確保編碼數據的合理性和科學性，本研究首先根據數學關鍵能力評價指標框架和數學試題綜合難度模型框架分別對此次適應性測試數學試題進行數據編碼，再將所得數據委托另外兩位專家進行復審，其中1人是中小學正高級教師，另1人是近年來負責廣西高考數學學科質量分析專家，收回兩位專家的修改意見后再次進行校對、分析和討論，最終確定了本研究的編碼數據矩陣，進而計算出所有試題的綜合素養水平和綜合難度系數，最后進行比較分析。

（一）適應性測試題綜合素養水平的具體分析

依據表1，采用喻平的數學關鍵能力評價指標框架得到2024年全國適應性考試卷數學關鍵能力評價雙向細目表，并根據綜合素養模型公式計算得到各試題的綜合素養水平（用字母d表示，如表3所示）。

由表3可知，2024年全國適應性測試數學卷共19道大題，統計時解答題小題單獨進行統計，合計25個問題，覆蓋單項選擇題、多項選擇題、填空題和解答題四個部分。首先，涉及六大數學學科核心素養及三個水平考查點數合計為90個“√”，其中各核心素養的第一水平共37處，第二水平共32處，第三水平共21處，可見此次適應性測試題主要集中在核心素養的第一、第二水平的考查。其次，關于六大核心素養的考查情況為：數學運算（24處）、邏輯推理（22處）、數學抽象（18處）、直觀想象（13處）、數學建模（10處）、數據分析（3處），主要考查了數學運算、邏輯推理和數學抽象等三個素養。最后，六大核心素養考查三個水平的綜合素養水平為：數學運算（92分）、邏輯推理（66分）、數學抽象（48分）、直觀想象（43分）、數學建模（28分）、數據分析（3分），突出考查了數學運算的第三個水平，數學抽象及邏輯推理的第一個水平，其中數據分析素養考查權重最少。

綜合表3中最右側綜合素養水平的數據可知，單項選擇題、多項選擇題、填空題和解答題的綜合素養水平均呈遞增趨勢，分別于第8題、第11題、第14題和第19題達到最大值。其中綜合素養水平最大的為第19題，該題綜合考查新定義與初等數論的知識，該題情境新穎，思維強度高，側重考查學生對新定義的理解和利用新符號的推理過程，綜合難度非常大；其次是第18題，該題進一步加強了解析幾何中幾何性質的考查，減少數值的計算，更深入考查了學生的思維能力，綜合難度也非常大；再次是第14題，該題考查了不等式組，涉及3個參數，5個變量，考查學生利用線性規劃思想討論一類最大最小問題，由于該題沒有直接指明應用的背景，導致大量學生不清楚試題考查的意圖而無從下筆。

（二）適應性測試題綜合難度系數的具體分析

依據表3，采用鮑建生的數學試題綜合難度模型框架得到2024年全國適應性測試卷數學試題綜合難度雙向細目表，并根據綜合難度模型公式計算得到各試題的綜合難度系數（用字母f表示，如表4所示）。

由表4可知，2024年全國適應性測試數學卷單項選擇題、多項選擇題、填空題和解答題四個部分的綜合難度系數一共出現了四個峰值，分別在第8題（難度系數為19）、第11題（難度系數為19）、第14題（難度系數為23）和第19題（難度系數為26.4），并且每一部分內部試題綜合難度系數呈遞增趨勢，說明此次適應性測試各部分的試題難度設計由易到難，考查要求由淺入深，突出基礎，兼顧選拔。

綜合表4中數據，5個關鍵能力及各水平考查情況為：推理能力（99.7分）、運算水平（80分）、認知水平（53分）、知識含量（37.7分）、情境因素（23分），主要突出了推理能力的考查。一是在“情境因素”維度，“數學情境”層面有22個問題，“現實情境”層面有3個問題，沒有“科學情境”層面問題，絕大部分問題集中在純數學情境，這些蘊含于數學知識與問題解決過程的數學情境，突出考查學生提出問題、分析問題和解決問題的能力。二是在“認知水平”維度，“理解”層面有9個問題，“運用”層面有11個問題，“分析”層面有5個問題，大部分問題集中在理解和運用層面，考查學生使用基本概念進行知識遷移并解決具體問題的能力。三是在“運算水平”維度，“簡單數值運算”層面有3個問題，“復雜數值運算”層面有4個問題，“簡單符號運算”層面有13個問題，“復雜符號運算”有5個問題，大部分問題集中在符號運算層面，考查學生依據運算法則解決問題的能力，包括理解運算對象、掌握運算法則、探究運算思路和求得運算結果。四是在“推理能力”維度，“簡單推理”層面有10個問題，“復雜推理”層面有15個問題，復雜推理層面的問題多于簡單推理，考查考生掌握推理的基本形式和規則、探索和表述論證過程、有邏輯地進行表達和交流的能力。五是在“知識含量”維度，“1個知識點”層面有14個問題，“2個知識點”層面有8個問題，“3個及以上知識點”層面有3個問題，大部分試題僅圍繞單個知識點進行考查，僅少量問題存在跨章節和跨學科的知識參與的現象。

（三）適應性測試題綜合素養水平和綜合難度系數的對比分析

為了更加直觀地呈現2024年全國適應性測試題的綜合素養水平和試題綜合難度系數的變化關系，本研究以題號為橫坐標，以每個題目的綜合素養水平及綜合難度系數為縱坐標，繪制了綜合素養水平和綜合難度系數的折線圖，并生成了綜合素養水平和綜合難度系數的趨勢線（如圖1所示）。

圖1 2024年全國適應性測試數學試題

綜合素養水平和綜合難度比較圖

由圖1可知，此次適應性測試數學試題的綜合素養水平和綜合難度系數兩條曲線的整體走勢大致相同，四大題型出現的峰值和峰谷位置也大致相同，分別是單項選擇題第8題，多項選擇題第11題，填空題第14題和解答題第18題、第19題，這四題的綜合難度最大，考查的綜合素養水平最高。且隨著題號的增加，兩條曲線的趨勢線也越來越靠近，說明試題的綜合素養水平越高和試題的綜合難度系數越接近。同時，我們也發現兩條曲線出現異常的點在第4題和第16題，分別考查了空間中點、線、面位置關系和概率計算問題，之所以出現異常，可能是在對適應性測試題的五個難度因素和六個核心素養水平進行解構時存在主觀因素誤解造成。

三、結論與備考啟示

（一）結論

2024年全國適應性測試數學試題的綜合難度系數非常大，考查學生的綜合素養水平非常高。由折線圖可以看出，試題的綜合難度系數與綜合素養水平兩者的變化趨勢大致相同，可見，試題的綜合難度系數越大，對學生的綜合素養水平要求也越高。此次測試在單項選擇題、多項選擇題、填空題和解答題四大題型的最后一題均出現了峰值，可見，測試卷在四大題型的最后一題均設計了一道難度非常大的壓軸題來進行把關，在技術上解決了對數學學科拔尖學生的考核和選拔，符合國家戰略。試題還突出考查了學生的數學運算、邏輯推理和數學抽象等三大素養，突出學生對數學學科本質的理解，強化學生對數學基本思想的學習，要求學生學會以專家思維分析問題、解決問題進而提出問題。

（二）備考啟示

1.深化基礎，強化對數學學科本質的理解

高考命題進一步深化基礎性考查，這里的“基礎性”指的是“‘基礎知識的學習、‘基本方法的掌握、‘基本能力的提高、‘基本態度與價值觀的養成”［2］。從此次適應性測試題的綜合難度雙向細目表來看，全卷共19道題，其中有9道題的難度系數在15及以下，占比47.37%，有14道題的難度系數在17及以下，占比達73.68%，這樣的比例分布符合高考命題深化基礎性考查的趨勢。因此，無論在教學過程中還是測試卷的命制過程中，教師都應著力夯實學生的基礎，加強基礎知識的鞏固、基本方法的掌握、基本技能的培養。我們在備考時應回歸教材與《課程標準》，引導學生對數學知識內容本質的理解，深挖教材中的例題以及課后練習所蘊含的數學本質及內在聯系，從教材的例題、習題出發，恰當地設計變式題，幫助學生鞏固對數學概念的理解，強化對通性通法的融會貫通及應用，培養學生透過現象挖掘數學本質并以其為基礎、借助通性通法解決數學問題的基本能力。備考應杜絕題海戰術，讓學生扎實地學、精致地學，助力國家“雙減”政策的落實。

2.注重素養，強化對數學教育內核的追求

數學高度的抽象性、邏輯的嚴密性和廣泛的應用性，分別指向學生的“抽象、推理和模型”三大數學基本思想，即抽象能力、推理能力和應用能力，承載了獨特的、鮮明的學科育人價值，是數學學科核心素養，也是數學教育的內核［7］。由于其可教、可學的特性，在備考過程中，教師要強化對數學基本思想的培養。如測試卷第11題通過抽象函數考查學生邏輯推理能力，第18題通過借助幾何圖形的剪貼拼接，考查學生尋找等量關系把復雜的三角形面積問題轉化為簡單的四邊形面積問題的模型轉化思想，第19題通過新定義問題考查學生理解新定義、利用新符號展示問題解決過程的推理能力。因此，高考備考要注重問題解決的綜合性、應用性、創新性，要突出數學抽象、邏輯推理和數學建模素養的培養，同時要調整數學四大題型壓軸題的備考策略，不再適用傳統“壓軸題”的策略，而是要注重素養，突出創新能力和批判思維的培養，強化對數學教育內核的追求。

3.優化教學，強化對數學思維能力的培養

保繼光指出：學習數學不是以懂多少數學公式為目標，而是要鍛煉解決問題過程中所用到的思維方法，也就是數學思維。有良好數學思維和素養的人，是善于獨立思考的人，在解決問題的過程中更具創造力。高考是國家選拔未來高科技創新人才的重要工具，為服務于國家的戰略需要，高考數學試題的命制，以選拔出具有數學思維和素養的人才為目標。因此，在備考過程中，教師應摒棄套路化教學，著重關注學生在解決數學問題時思維的活動歷程，通過問題解決引導學生深入思考，在課堂教學中給學生預留足夠的時間思考解決問題的方式方法，敢于把課堂還給學生，讓學生在試錯的過程中思維得到碰撞交融并進一步提升，幫助學生從題海戰術中解放出來，如此方能讓學生的數學學科核心素養得到長足發展。

毋庸置疑，2024年全國適應性測試數學試題的命題風格、試卷結構、難度系數、綜合素養水平代表著高考改革的方向，將在2024年新高考中全面體現，2024年高考試題的命制必將突出立體化檢測功能。對廣大師生而言，要尊重高考試題的基礎性設定，夯實基礎，突出學科素養培養，摒棄套路化教學，積極開展教學改革。高考命題改革，變是大勢所趨，這需要教師們擁抱變化，積極準備。

參考文獻

［1］中華人民共和國教育部.普通高中數學課程標準（2017年版）［M］.北京：人民教育出版社，2020.

［2］雷新勇.大規模教育考試科學屬性之理論和實踐思考［J］.教育與考試，2007（1）：31-37.

［3］喻平.數學核心素養評價的一個框架［J］.數學教育學報，2017（2）：19-23+59.

［4］喻平.基于核心素養的高中數學課程目標與學業評價［J］.課程·教材·教法，2018（1）：80-85.

［5］呂世虎，于麗芳，王尚志.數學試卷綜合難度的內涵及其指標體系建構［J］.數學教育學報，2020（4）：1-6.

［6］鮑建生.中英兩國初中數學期望課程綜合難度的比較［J］.全球教育展望，2002（9）：48-52.

［7］曹培英.從學科核心素養與學科育人價值看數學基本思想［J］.課程·教材·教法，2015（9）：40-43+48.

注：本文系2021年度廣西教育科學規劃課題“鄉村振興戰略背景下數學教師單元教學能力提升的策略與實踐研究”（2021ZJY190）、南寧市“十四五”規劃2022年度教育科學規劃課題“深度教學視域下初中數學單元教學設計研究”（2022C398）的研究成果。

（責編 林 劍）