基于數學思想滲透的數學解題教學研究

白楊

摘? 要：解題是數學的構成要素，高中數學教師需要關注解題教學的開展，并聯系高考的實際題型和新課標的教學要求做出綜合設計。在過去的教學中，教師雖然也非常重視解題教學，但常采用題海戰術來推動學生進行解題，這樣的教學設計對學生的發展較為不利，也影響了學生的成長。在當前，為了貫徹新課標的教學優化理念，設計更加高效合理的數學解題教學，教師要關注數學思想滲透的價值，從教學調整入手，研究將數學思想滲透到高中數學教學中的具體方法。

關鍵詞：數學思想；高中數學；解題教學

一、做出概念詮釋，解讀數學思想

數學思想是數學的精髓所在，但學生從字面上難以理解數學思想，更難以從中找出解決數學問題的實際方法。為了讓學生了解數學思想，并為其解題應用創造基礎，教師在教學實際中需要對數學思想的概念進行詮釋，為學生解讀數學思想的構成。在學生對數學思想有了基本了解后，教師就可以為學生進行進一步展示，引領其使用數學思想來探索解題的實際方法。

如教師可以在實際中用數形結合思想為學生做出解讀，讓學生了解數學思想的概念，并初步了解其在解題中的應用價值。具體而言，教師可以先為學生闡述數學思想的概念：“數學思想，是指現實世界的空間形式和數量關系反映到人們的意識中，經過思維活動而產生的結果。”在展示了概念后，教師可以結合12個常見的數學思想為學生做展示，幫助其理解概念。為幫助學生了解，教師可以從數與形的關系出發，體現“數無形，少直觀，形無數，難入微”，利用“數形結合”可以使所要研究的問題化難為易，化繁為簡的解析讓學生明確代數和幾何知識相結合進行解題的價值。在實際中，教師可以簡要展示下述例題，幫助學生加深認知：

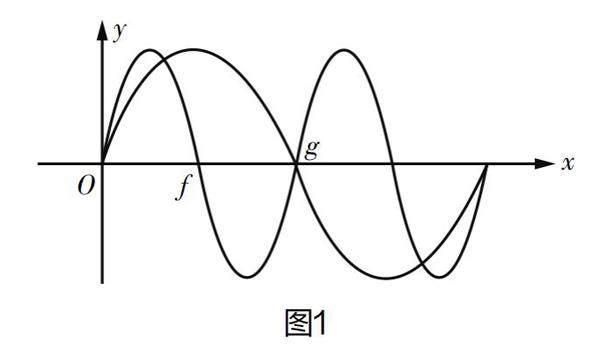
例題1：方程ｓｉｎ２ｘ＝ｓｉｎｘ在區間（０，２π）解的個數為? ?（）。

Ａ． １? ? Ｂ． ２? ? Ｃ． ３? ? Ｄ． ４

在展示出該題目后，教師可以引導學生聯系二倍角公式進行習題化簡，讓學生做出解讀，然后結合三角函數知識，嘗試繪制以下圖像（見圖１），然后借助讀圖分析，推斷ｓｉｎ２ｘ和ｓｉｎｘ的值，進而求出題目所要求的內容。在學生完成解讀后，教師需要根據學生的實際回答情況做出簡單的評書，為學生展示數形結合的意義和方法，幫助學生理解數形結合的概念。如此，教師就可以讓學生初步了解數形結合數學思想在函數習題中的應用價值。

二、展示范例習題，引導學生認識

為幫助學生利用數學思想解答數學習題，教師可以在實際中展示范例習題，借助這些習題引導學生初步認識數學思想在數學題解答中的具體應用要求。為做好這一解析展示工作，教師需要利用課下時間做出研究，找出適宜作為展示對象的習題，然后選擇一個合適的形式展示出來，再引導學生做出解讀。

如在教學實際中，教師可以結合習題的選用做出展示，讓學生了解相關數學思想在數學解題中的應用：

例題１：（函數方程思想）建造一個容積為８ｍ３，深為２ｍ的長方體無蓋水池，如果池底和池壁的造價每平方米分別為１２０元和８０元，則水池的最低造價為＿＿＿＿＿＿。

解析：函數思想，是指用函數的概念和性質去分析問題、轉化問題和解決問題。方程思想，是從問題的數量關系入手，運用數學語言將問題中的條件轉化為數學模型，進而解決相關問題。在實際的解題中，函數思想常會與方程思想融合運用實現解答。需要注意的是，通過函數方程思想解答數學問題是利用相關的概念和性質去解決現實問題，而非解答函數方程問題。對該題目而言，其考查點在于對函數模型的選擇運用，在實際的解題中可以使用函數方程思想做出習題解析，引入數學符號建立數學模型，進而使用解答函數習題的方法完成該題目，解答過程如下：

設長為ｘ，則寬為４／ｘ，造價ｙ＝４×１２０＋４ｘ×８０＋１６／ｘ×８０≥１７６０，當且僅當：４ｘ×８０＝１６／ｘ×８０，即ｘ＝２時取等號。因此該題目的答案為１７６０。

教師解析：“本題考查對函數模型的選擇與應用，在題目的解答中，同學們需要先審題，找準題目中的條件和關鍵因素，完成未知數的設列。在完成基本整理后，再引入數學符號，建立數學模型。在解答時，同學們需要使用解方程的方法得出數學結果。在這一題中，題目涉及了函數方程思想、分類討論思想、整體思想，同學們知道這些數學思想的運用都體現在哪些地方嗎？”

通過上述案例的展示，函數方程思想、分類討論思想、整體思想就可以很好地體現出來，教師也可以引導學生實現基本認知。在實際的教學中，針對其他數學思想，教師也應做出解答展示。

三、結合具體思想，展現解題案例

在實際的解題教學開展過程中，為了讓學生掌握具體的教學方法，針對習題進行具體的案例解析是必不可少的，教師需要借助這些解題案例引導學生分析解題的過程，找出運用數學思想的方法途徑。在這一解析過程中，教師除了需要注意習題的展示和簡要解析，還需要注意引導性語言的運用，借助簡單的提問，推動學生進行思考，以此幫助學生加深對數學思想的了解。

如為了幫助學生深入解析并理解數學思想，教師需要設計解題案例的組合，幫助學生進行觀察分析，以此實現學生對知識的透徹認知和掌握。如對整體思想，教師可以選用以下幾類習題進行展示，幫助學生透徹了解：

例題１：已知２ｍ－３ｎ＝－４，則代數式ｍ（ｎ－４）－ｎ（ｍ－６）的值為＿＿＿＿＿＿＿。

在展示出上述習題后，教師可以先讓學生嘗試著解答，然后再根據學生的解答情況做出解讀，引領學生認識整體思想，并使用整體思想對題目做出系統梳理。在進行案例展示的過程中，教師需要為學生展示完整的解題流程，并強調其中的整體思想和實際應用要點。以例題１為例，教師可以采用如下方式進行解讀：

師：“通過簡單的讀題，同學們可以發現這個題目屬于什么類型呢？”

生：“代數式化簡求值。”

師：“回答得很好，那么這一類題目的解題要點在哪里呢？”

生：“化簡式子，將代數式ｍ（ｎ－４）－ｎ（ｍ－６）化簡為包含２ｍ－３ｎ的式子。”

師：“根據整體思想，我們可以將原式拆解開，然后通過將２ｍ－ｎ看作一個整體完成化簡。”

上述的教師引領與展示過程可以推動學生對數學思想的理解，讓學生認識運用數學思想解決數學問題的方法，這對學生解題能力的發展有著較強的推動作用。

四、進行系統梳理，明確解題要素

在完成基本的數學思想解析并幫助學生認識運用思想方法解決數學問題的具體途徑后，教師在教學中，便需要從系統梳理出發，設計進一步的教學過程。在實際應用中，系統梳理是為了幫助學生認識數學思想對應的習題類型，將相關的習題做出分類處理，然后運用數學思想解答數學習題的要素進行總結與整理，形成行之有效的解題過程，推動學生的提升與發展。在這一過程中，教師要關注習題的展示，并督促學生進行總體思考，整理相關習題，以此實現有效引導。

如在實際教學中，教師可以針對數形結合思想做出整理，引導學生系統分析，進而使學生明確借助數形結合思想解答幾何圖形問題的現實方法。其中，教師可以做出列舉：數形結合可以解決集合問題，在集合運算中使用數軸處理集合的交、并、補的過程，便是使用數形結合解析數學問題的現實過程；利用數形結合可以解決函數問題，從函數的圖像關系出發聯系解析式，是解讀函數解答的有效方法等。

在完成上述知識的論述后，教師可以建立簡要的框架圖，對相關內容做出整理，幫助學生梳理和記憶，為實際解題應用創造條件。如此一來，教師可以幫助學生進一步認識數學思想在數學解題中的實際運用方法，這對學生數學解題能力的發展有著較強的推動作用，也能讓學生更好地找準解題的要點。

五、設置變式訓練，推動解題運用

變式訓練的開展有利于提升學生的解題能力，也可以加強學生對相關知識技能的有效掌握。在例題學習中，學生雖然可以跟隨教師的講解與分析對習題產生基本認知，但難以真正做到理解與掌握，在遇到相似習題時，也可能會出現不能解答的情況。為解決這一問題，促進學生的發展，教師在教學實際中需要優選練習題，并針對性地擬定變式題目，再將相關的題目一并展現給學生，讓學生借助這些題目進行解題練習，發展自身的解題能力。

如在實際教學中，教師可以針對討論思想的運用來展示習題與其變式題，幫助學生掌握解題的具體方法。其中，教師可以選用如下習題：

原式：在同一平面上，∠ＡＯＢ＝７０°，∠ＢＯＣ＝３０°，射線ＯＭ平分∠ＡＯＢ，ＯＮ平分∠ＢＯＣ，求∠ＭＯＮ的大小。

變式：已知∠ＡＯＢ＝６０°，過Ｏ作一條射線ＯＣ，射線ＯＥ平分∠ＡＯＣ，射線ＯＤ平分∠ＢＯＣ，求∠ＤＯＥ的大小。

在展示該題目后，教師可以引導學生進行思考，分析分類討論思想的運用。為了推動學生的進一步發展，教師還需要做出延展，設計學生擬題環節，讓學生從該題目入手嘗試著進行拓展構題，生成相關聯的變式題。在這一擬題思考的過程中，學生的思想可以得到拓展，解題能力也能得到進一步提升。

六、解讀高考真題，實現知識內化

高考是學生人生中的第一大考，也是高中階段需要面臨的一大挑戰，學生能否通過高考的考查并考取心儀的大學，會直接影響到其未來發展。基于這一現實問題，高中數學教師需要認識到自己的教學職責，想辦法借助教學的有效設計幫助學生發展解題能力。在實際教學中，教師可以選擇一些高考真題做出展示和講解，讓學生對這些真題進行分析解讀，嘗試使用數學思想延伸出的解題方法進行有效解答。在這一過程中，學生不但可以實現數學思想解題知識的內化，還能熟悉并掌握高考題目，做好迎接高考的準備。在完成高考題的練習后，教師便可以引領學生進行探究學習，推動學生掌握數學思想。

七、結語

總而言之，數學思想作為數學的精髓所在，將其引入數學解題教學中，可以幫助學生更好地認識數學解題方法，加深對知識的理解程度。在高中教學實際中，為發展學生的數學解題能力，增強其習題認知，教師要利用課下時間進行研究，分析數學思想的構成與其在相關習題解題中的實際應用，然后從學生的解題認知出發，分析幫助學生認識并掌握使用數學思想解讀實際數學習題的現實方法。在教學實際中，教師可以圍繞數學思想解讀、范例習題展示、解題案例展示、系統梳理知識、變式訓練設置、高考真題訓練六個方面來做出系統構建。