基于結構化教學的高中數學“主題—課時”教學設計

朱坤密 李德安 孫雪梅 羅蕊

［摘? 要］ 數學結構化教學能讓學生用整體、全局、聯系的視角把握數學知識體系，從而形成良序的知識結構，養成良好的數學思維方式.文章提出高中數學“主題—課時”教學設計框架：在教材分析時，一找“三點”（找到新知的“起點”，新舊知識的“連接點”，思維的“突破點”）；二理“三線”（梳理“知識主線”，尋找“方法主線”，提煉“素養主線”）. 根據“三點”“三線”，在教學環節的設計中使知識結構化、方法結構化、過程結構化，利于學生實現知識、經驗、思想方法的正遷移，從而促進學生認知結構及數學學科核心素養的發展.

［關鍵詞］ 結構化教學；教學設計；核心素養

布魯納在其著作《教育過程》中指出：要掌握事物的結構，因為條理有序，整體性強的知識結構，很容易被學生掌握和記憶，因此，充分培養學生邏輯性和整體性思維，可以提高他們的學習效率，促進對知識的理解、概括［1］. 《普通高中數學課程標準（2017年版2020年修訂）》明確提出：要突出數學主線，凸顯數學的內在邏輯和思想方法；要引導學生整體把握教學內容，促進學生數學學科核心素養的形成和發展［2］.

結構化是一種思維方法，著重于對事物內部基本結構的探索，力求認識事物的基本要素和要素之間的基本關系，從而探索事物內在的基本規律［3］. 數學結構化教學能讓學生用整體、全局、聯系的視角把握數學知識體系，從而形成良序的知識結構，養成良好的數學思維方式，便于學生實現知識、經驗、思想方法的正遷移，進而能舉一反三、融會貫通，促進學生認知結構和數學學科核心素養的良好發展.

“主題—課時”教學是指以某一主題（如“函數”主題）為大單元下的某一具體章節（如4.2.1指數函數的概念）的教學（主要針對課時新授課教學）. 本文基于結構化教學的相關理論和多年的教學實踐，提出高中數學“主題—課時”教學設計框架：在教材分析時，一找“三點”（找到新知的“起點”，新舊知識的“連接點”，學生思維的“突破點”）；二理“三線”（梳理“知識主線”，尋找“方法主線”，提煉“素養主線”）. 根據“三點”“三線”，通過“明線”（情境、問題、知識、活動等）和“暗線”（思想、方法、素養等）的形式貫穿整個教學過程，在教學環節的設計中使知識結構化、方法結構化、過程結構化，從而讓學生的數學學習能夠置于結構組織中，便于學生擁有一個整體的認知框架，能較好地促進學生思維品質和數學學科核心素養的發展.

下面以人教A版普通高中數學教科書（2019版）必修第一冊（下文簡稱“課本”）“4.2.1指數函數的概念”為例，談談“主題—課時”教學設計框架的應用．

找“三點”

新知的“起點”是指學生的“現實起點”和“認知起點”. “現實起點”與學生的生活實際、學習及生活經驗等相關. 本節課，學生在以往學習中接觸過人口增長問題、細胞分裂問題、放射性物質衰減問題等，在新聞報道中聽過指數增長、指數爆炸等詞，這些都是學生的“現實起點”. 因此，可選擇細胞分裂或病毒傳播或碳14衰減等問題情境作為新課導入實例. “認知起點”是指學生的知識、技能以及認知經驗等基礎. 本節課，學生的“認知起點”在函數及冪函數概念學習的基礎上展開，在前面的學習中，學生經歷概念抽象的過程，具有通過對具體實例共性的歸納，進而再抽象概括的經驗.

學生在新課學習中，舊知、思維、經驗與新知會出現“斷層”的現象，因而產生認知缺失或認知沖突. 想要解決這個問題，就需要有知識的聯系、經驗的鏈接或者思維的變換，這些就是新舊知識的“連接點”. 在教學中，要引導學生找到新知與已有知識和經驗的連接點和結合點. 指數函數概念是課本第四章第二節第一課時的教學內容，安排在函數、冪函數、指數冪等知識之后，與函數概念、冪函數概念之間具有從屬、并列的關系，這些都是新舊知識的“連接點”. 因此，教學中可類比函數概念、冪函數概念的學習來建構指數函數的概念，同時讓學生注意指數函數與函數的上下位關系以及與冪函數在形式上的區別.

在數學教學中，數學概念的形成、運算法則及定律的探究、規律的總結、公式的推導、解題方法的揭示等都是學生思維的突破點. 在學習本節課之前，雖然學生對函數、冪函數的概念有了一定的了解，對冪ax（a>0）也有了一定的認識，但對指數函數的學習仍然有一定的畏懼感． 此外，高一學生的數學建模能力比較薄弱，對實際問題的解決有無助感. 因此，這些既是學生的“痛點”，也是學生思維的突破點.

理“三線”

從學習論的角度來看，學習的過程就是一個概括化的過程，越是概括化、結構化的知識就越具有遷移應用價值［4］.

梳理“知識主線”既要關注同一單元內容之間的邏輯關系，又要關注同一主題內容之間的邏輯關系.把章節內容置于同一單元內、同一主題內進行縱橫聯系和梳理，從不同視角對知識進行系統感知，并形成有序的、立體的、動態的整體結構，從而把零碎的、孤立的知識由點串成線，由線連成面，由面形成體.

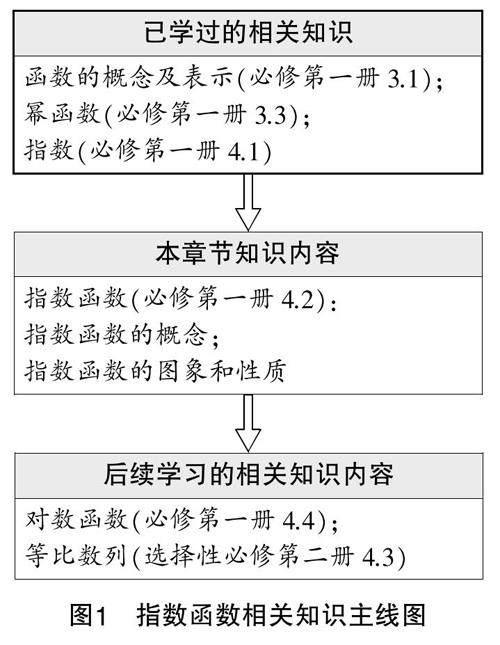
教師可以通過“導學案”將知識主線圖呈現給學生（指數函數相關知識主線圖如圖1所示），也可以讓學生自己畫出章節知識結構圖. 讓學生從整體、從全局系統把握所學章節知識與前后相關知識的聯系，以及它所具有的或承上啟下或基礎鋪墊或拓展延伸的作用.

“方法”主線一是指相關單元、相關主題共同的研究路徑和方法，二是指本章節數學知識蘊含的通法通性以及具有一般性的數學思維方式.指數函數是基本初等函數之一，對它的研究遵循“背景—概念—圖象與性質—應用”的基本路徑和思路. 前面學過一般性的上位概念——函數. 函數的概念是通過概念形成的方式引入的，即先對具體實例進行共性分析，抽象概括出函數的定義，并用數學語言下定義，然后通過概念辨析，深入理解函數概念的內涵，從而讓學生經歷和感受“具體函數—一類函數—函數概念一般化”逐步抽象的過程. 通過對冪函數概念的辨析，學生領會了通過具體實例（正例和反例）進一步理解概念的關鍵詞（或語句）的含義，能正確區分相似概念的方法. 這些都為指數函數概念的學習提供了方法指導.

本章節的學習要讓學生理解函數是描述客觀世界中變量關系和規律的最為基本的數學語言和工具，學會用圖象和代數運算的方法研究函數，理解函數中所蘊含的運算規律，并會用這些函數建立模型解決實際問題［5］. 因此，本章節以及本課題的“核心素養線”主要涉及數學抽象、數學建模、直觀想象、數學運算和數據分析等核心素養.

教學過程設計

基于對指數函數概念“三點”“三線”的分析，下面呈現的是相應教學過程設計片段.

1.？搖創設情境，實例導入

情境創設：（1）播放某地區病毒傳播的新聞報道，并展示病毒感染人數圖片.

（2）引用課本第四章的引言：考古學家利用良渚遺址中遺存物碳14的殘留量測定遺址年代.

通過對兩個實例的呈現，引入課題：病毒傳播的研究以及考古學家測定遺址年代時所用的數學知識就是今天要學習的指數函數.

設計意圖 通過對學生的“現實起點”的分析，用現實中的實例引入新課，讓學生明確為什么要學習指數函數，同時激發學生的求知欲.

2. 歸納概括，抽象概念

問題呈現：（1）《莊子·天下篇》中說道：“一尺之棰，日取其半，萬世不竭.”請寫出取x次后，木棰的剩余量y與x的關系式.

（2）將一張A4紙不斷對折，請寫出對折x次后，紙的層數y與x的關系式.

（3）閱讀課本第113頁的問題2后，請寫出生物體內碳14含量y與死亡年數x的關系式.

列表觀察：如表1所示.

類比思考：（1）函數的定義是什么？

（2）前面對函數和冪函數下定義時，采用的是什么樣的思維方式？ 結合學習函數和冪函數的經驗，應該如何學習這個新的函數？

（3）這三個函數的共同特征是什么？請寫出其一般形式.

形成概念：通過對上述三個問題的思考，采用引出函數和冪函數概念的思維方式“觀察例子—尋找共性—歸納概括—抽象定義”，使指數函數概念的引出水到渠成：函數y=ax（a>0，且a≠1）叫做指數函數，其中指數x是自變量，定義域是R．

概念理解：（1）比較指數函數與冪函數的表達式的異同.

（2）類比一次函數、反比例函數、二次函數、指數函數一般形式中對相關常數的取值范圍的限制，請思考并討論指數函數y=ax中的常數a為什么要限制“a>0，且a≠1”？

（3）呈現正反例，通過辨析判斷，進一步理解并掌握指數函數的概念和本質特征. 判斷下列說法的對錯.

①y=是指數函數．（? ）

②y=x2是指數函數． ? （? ）

③y=2-x不是指數函數． （? ）

（4）呈現課本第114頁的例1，指導學生聯想求函數表達式常用的待定系數法及方程思想，先求得指數函數的表達式，再求得相應的函數值.

設計意圖 一方面，改變教材中的引例——通過對三個問題的探討作為引例，類比函數和冪函數概念的抽象，引導學生觀察三個函數的共性并歸納概括，抽象出指數函數的概念，進一步培養學生數學抽象核心素養． 另一方面，通過復習舊知，找到新舊知識的“連接點”，并通過對指數函數和冪函數概念以及表達式的對比學習，加深學生對指數函數內涵及外延的理解和判斷.最后，利用（3）（4）兩道例題，一是促進學生對指數函數概念本質的理解和掌握，二是回顧舊知，加強新舊知識的聯系. 在教學中，通過遷移、類比、聯想，讓學生感受數學的整體性及系統性.

3. 模型建立，拓展應用

提出問題：呈現課本第111頁的問題1和第113頁的問題2，引導學生建立指數函數模型來解決實際問題.

問題1 略，詳見課本第111頁.

（1）比較A，B兩地景區游客人次的變化情況，有怎樣的變化規律？

（2）如果游客平均出游一次可給當地帶來1000元的門票之外的收入，A地景區的門票價格為150元，B地景區沒有門票，比較這15年間A，B兩地旅游收入的變化情況.

建立模型：（1）引導學生將表中的數據直觀化：根據表格中的數據，描點、連線，分別作出A地景區和B地景區游客人次隨時間變化的圖象，如圖2、圖3所示.

（2）對問題（1），引導學生觀察圖象，并用數學語言將A地景區和B地景區游客人次隨時間變化的規律表示出來：設經過x年后，景區游客人次為y，則A，B兩地景區y與x之間分別有什么關系？

對于A地景區，引導學生通過圖象觀察和數據分析，可得A地景區游客人次近似直線上升，年增加量約為10萬次，易得y=600+10x（x∈［0，+∞））.

對于B地景區，引導學生分組探究，通過對B地景區每年的游客人次做相應的運算：一些組做減法，一些組做除法.通過圖象觀察和數據計算，學生明白當每年游客人次的年增長量不同時，不能用“增長量”求出B地景區游客人次y與x的關系式，應該尋找“增長率”這個相同的量來刻畫此規律. 通過計算可知，經過x年后，B地景區游客人次是2001年的1.11x倍，即y=278×1.11x（x∈［0，+∞））.

對于B地景區游客人次的變化規律，有了前面的探討和指數函數概念的學習，要探究y與x之間的關系，還可直接告知B地景區游客人次是指數增長，圖3是指數型函數圖象，可假設y=278ax. 引導學生用待定系數法和方程思想來求函數表達式：由題目中的數據和圖象可知，當x=1時，y=309，即309=278a，解得a≈1.11，所以y=278×1.11x（x∈［0，+∞））.

解決問題：對于問題（2），引導學生應用問題（1）得到的兩個函數解析式，畫出其圖象來分析這15年間A，B兩地景區旅游收入變化情況，并在此基礎上延伸出一般的指數增長模型：設原有量為M，每次的增長率為p，經過x次增長，該量增長到y，則y=M（1+p）x（x∈［0，+∞），p>0）．

設計意圖 由于教材中的問題1較難，因此教學設計時將其調到應用環節. 在分析和解決問題的過程中，引導學生通過分析數據和計算推理，找出規律，建立函數模型． 根據“素養主線”，在教學過程中要注意培養學生的數據分析、數學運算、數學建模等核心素養. 通過分組探究，讓學生學會用不同的方法尋找變化數據中的不變量，同時讓學生掌握增加量、增長率這兩個刻畫事物變化規律的重要量. 通過數學運算來培養學生的數據分析素養，讓學生養成數學思維思考現實世界. 這是學生思維的“突破點”，也是教學的“突破點”.

通過對問題1的分析和探究，滲透數學建模思想，讓學生初步感知數學建模的基本過程：在實際情境中，從數學的視角，發現和提出問題—建立和求解模型—檢驗和完善模型—分析和解決問題，使方法、過程結構化. 這既能為以后解決實際問題提供思路和方法，又能化解學生的“痛點”.

問題2 在課本第113頁的問題2中，某生物死亡10000年后，它體內碳14的含量衰減為原來的百分之幾？

呈現新概念：教師把問題1、問題2中出現的兩種指數函數模型概括為一個新概念——形如y=kax（k≠0，a>0，且a≠1）的函數稱為指數型函數.

設計意圖 對于問題1及問題2，教師引導學生利用指數函數模型分析和解決問題，讓學生感受函數在現實生活中的應用，進一步培養學生的應用意識，讓學生逐步會用數學語言表達世界. 另外，通過拓展延伸，讓學生由一種函數的學習遷移到一類函數的學習，同時掌握解決實際問題的基本思路：發現問題—提出問題—分析問題（找尋方法）—解決問題（模型建立）—拓展應用（模型應用）.

4. 反思總結，整體建構

（1）今天我們學到了哪些知識和思想方法？

（2）本節課的學習與哪些知識有聯系？回到知識主線圖，我們學習了什么？將要學習什么？

（3）本節課的學習應用了哪些研究方法或思維方式，體現了哪些數學學科核心素養？

（4）根據對多種函數的研究經驗，我們后續要如何研究指數函數？說說你的研究思路和方法.

設計意圖 通過對問題（1）（2）（3）的反思總結，讓學生梳理本節課所學到的知識、方法等，讓學生通過“主題—課時”學習能做到“瞻前顧后”“前呼后應”，進而形成完整的知識體系，并重構其認知結構. 通過對問題（4）的反思，一是為后續指數函數圖象和性質的研究做鋪墊，二是總結研究一種新函數的思路和方法：可從數的角度（定義和解析式）研究函數，也可從形的角度（圖象）研究函數.

基于結構化教學的高中數學“主題—課時”教學設計要遵循“整體性、聯系性、結構化”等原則，以知識結構、方法結構、素養結構為抓手，以點帶面，讓學生學會從一個知識點到一類知識群的學習，掌握解決一個問題到一類問題的數學思維方式，從而能達到觸類旁通、舉一反三的效果，促進學生認知結構和核心素養的發展和完善.

參考文獻：

［1］ 布魯納. 教育過程［M］. 邵瑞珍，譯. 北京：文化教育出版社，1982.

［2］ 中華人民共和國教育部. 普通高中數學課程標準（2017年版2020年修訂）［S］. 北京：人民教育出版社，2020.

［3］ 皮亞杰. 結構主義［M］. 倪連生，王琳，譯. 北京：商務印書館，2017.［4］ 王俊. 結構嘗試教學法［M］. 北京：首都師范大學出版社，2012.

［5］ 章建躍. 核心素養立意的高中數學課程教材教法研究（上冊）［M］. 上海：華東師范大學出版社，2021.